题解:P11955 「ZHQOI R1」覆盖
https://www.luogu.com.cn/article/20vbz4zk
对于一颗线段树,它的结构如图所示。一定是先有红色,再有绿色,再有蓝色,再有紫色。如果靠前的颜色没有那么靠后的颜色不可能出现。
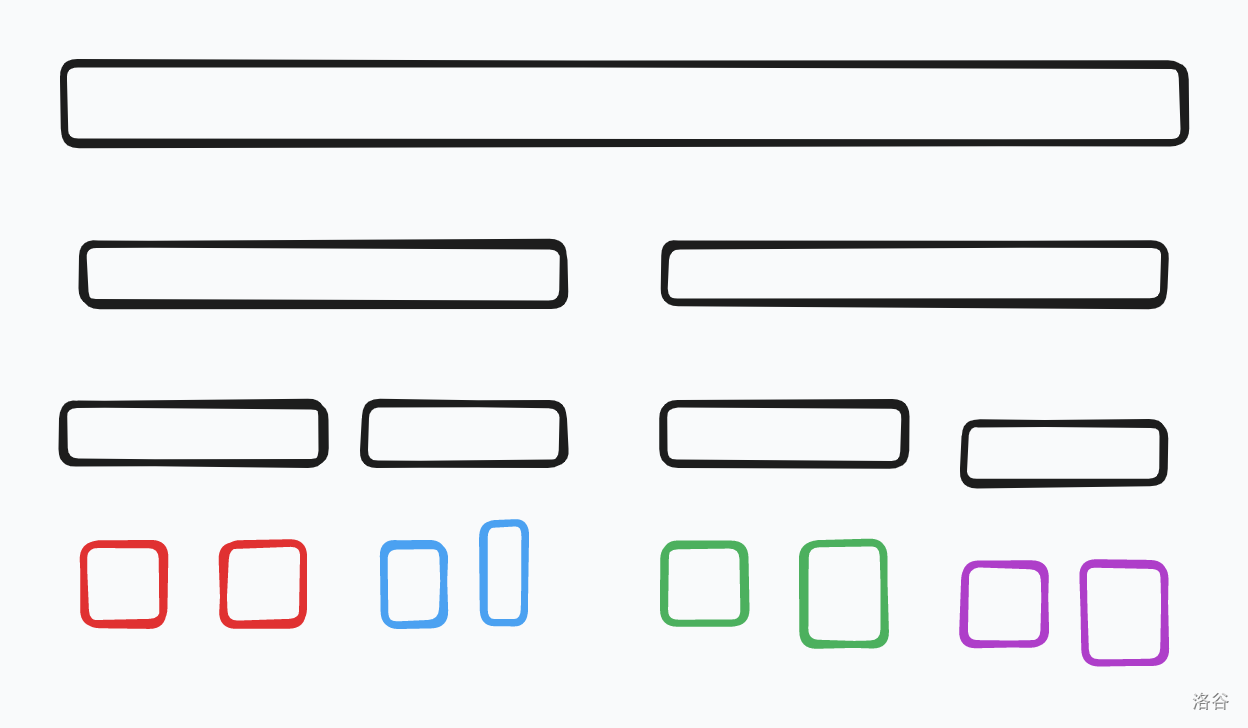
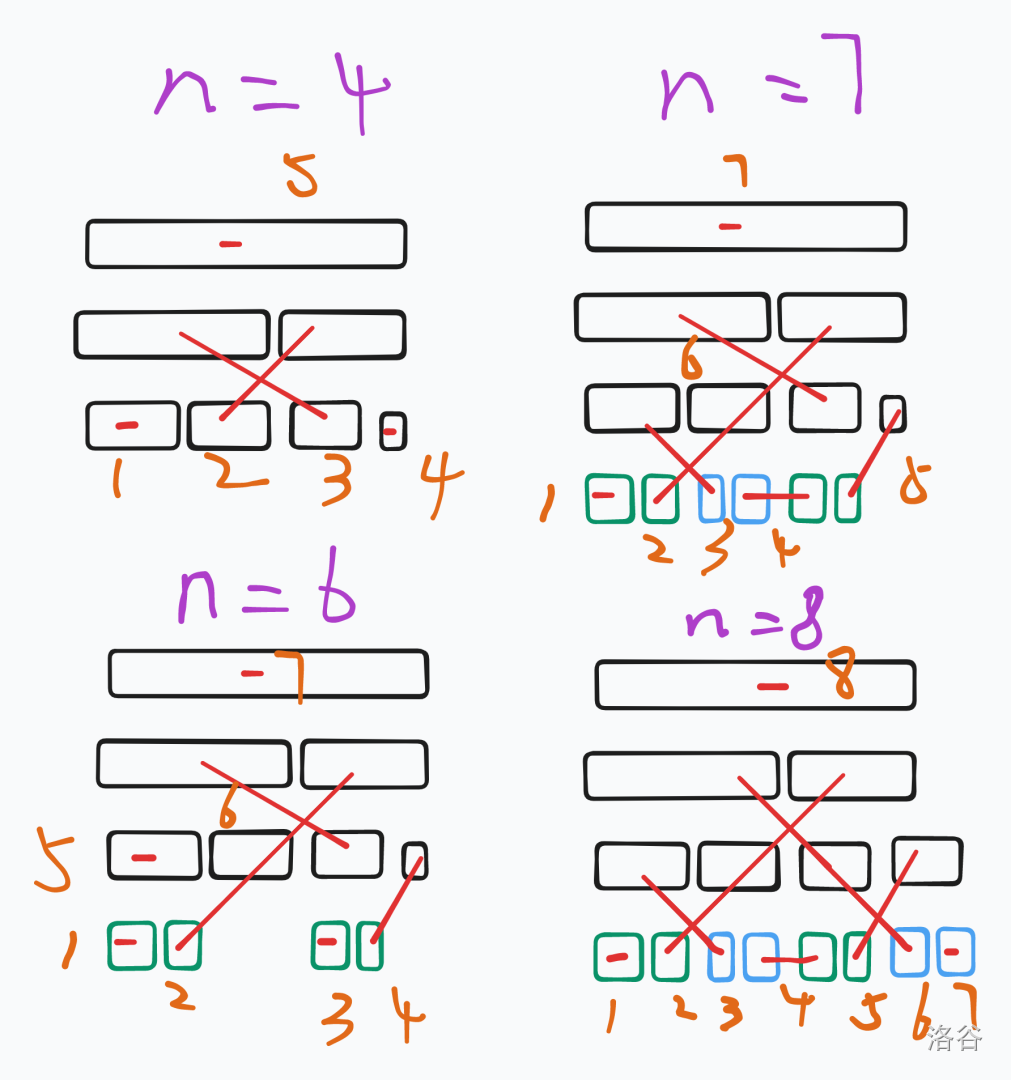
我们先考虑上一层(黑色)都已经处理完,新的一层会有什么影响,即已知 \(f_{2^j}\) 求 \(f_{2^j+k}\)。
设 \(y\) 为上层的节点个数(图示为 \(4\)),\(t=\frac{y}{2}\),\(x\) 为上层有儿子的节点的个数。
-
当 \(x\le t\) 时,如图 3,增加量为 \(x\)。因为对于每对新加的节点,他的右侧都可以和右上角组成一组,左侧单独需要多加一组询问。
-
当 \(t<x<y\) 时,如图 2,增加量为 \(t\)。因为每对蓝色节点的右侧可以和它的右边节点组成一组,蓝色节点的左侧可以和它的左上方组成一组。也就是,蓝色节点没有影响,增加量其实都是绿色节点贡献的。
-
当 \(x=y\) 时,如图 4,增加量为 \(t+1\)。因为最右侧节点需要单独一组,所以加一。
现在能 \(O(\log n)\) 求 \(f_i\) 了,从上往下每层去做即可。
现在所求的东西是 \(\sum f_i\)。发现每层增加的数是一个公差为一的等差数列加 \((f_{2^j}+t)\times (f_{2^j}+t-1)\),随便算算就行了。因为是赛时写的,我的具体实现是考虑每个 \(f_{2^j}\) 对后面的影响,直接提前加上。
复杂度 \(O(\log n)\)。
#include <bits/stdc++.h>
using namespace std;
#define IL inline
using ubt = long long;
template <typename T = int>
IL T _R() {
T s = 0, w = 1;
char c = getchar();
while (!isdigit(c)) w = c == '-' ? -1 : 1, c = getchar();
while (isdigit(c)) s = s * 10 + c - 48, c = getchar();
return s * w;
}
const int mod = 353442899;
IL ubt F(ubt p) { p %= mod; return p * (p + 1) / 2 % mod; }
IL ubt calc(ubt K) {
if (K <= 2) {
if (K == 0) return 0;
if (K == 1) return 1;
if (K == 2) return 1 + 3;
assert(false);
}
ubt now = 2;
ubt res = 1 + 3 * (K - 1);
while (now * 2 <= K) {
auto y = now >> 1;
auto det = F(y + 1) + y % mod * ((y - 1) % mod) % mod;
res += det;
res += (K - now * 2) % mod * ((y + 1) % mod) % mod;
res %= mod;
now <<= 1;
}
auto x = K - now;
if (x) {
auto y = now >> 1;
if (x <= y) res += F(x);
else {
res += F(y);
res += y % mod * ((x - y) % mod) % mod;
}
}
return res % mod;
}
IL void Main() {
auto L = _R<ubt>(), R = _R<ubt>();
auto res = (calc(R) - calc(L - 1) + mod) % mod;
printf("%lld\n", res);
}
int main() {
int Tims = _R();
while (Tims--) Main();
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号