[ABC266Ex] Snuke Panic (2D) 题解

[ABC266Ex] Snuke Panic (2D) 题解

前言

前几天看到了这个，发现自己还真没仔细思考过。

做了两道题，把这个题当个总结。

思路

设 \(f_i\) 表示：在 \(T_i\) 走到第 \(i\) 个节点的最大收益。

有转移：\(f_i=\max \{f_j\} + A_i\)。

其中 \(j\) 需要满足:

• \(y_j\le y_i\)
• \(T_i\le T_i\)
• \(|x_i-x_j|+y_i-y_j\le T_i-T_j\)

第三条限制可以转化为：\(x_i-x_j+y_i-y_j\le T_i-T_j \land x_j-x_i+y_i-y_j\le T_i-T_j\)。

容易发现满足第三条限制一定满足第二条限制，所以有如下限制：

• \(y_i\ge y_j\)
• \(x_i+y_i-T_i\le x_j+y_j-T_j\)
• \(-x_i+y_i-T_i\le -x_j+y_j-T_j\)

然后其实就是三维偏序了。因为这些点没有顺序限制，所以在外层可以排序掉一维，第二维可以用 CDQ 分治处理，第三为用树状数组即可。值得注意的是，因为有初始的点 \((0,0)\)，所以我们有 \(n+1\) 个点，离散化后树状数组应该跑到 \(n+1\)。

CDQ 实现的时候为什么和平常写的不太一样？

这里的“平常”指先把左右都递归下去再算贡献。

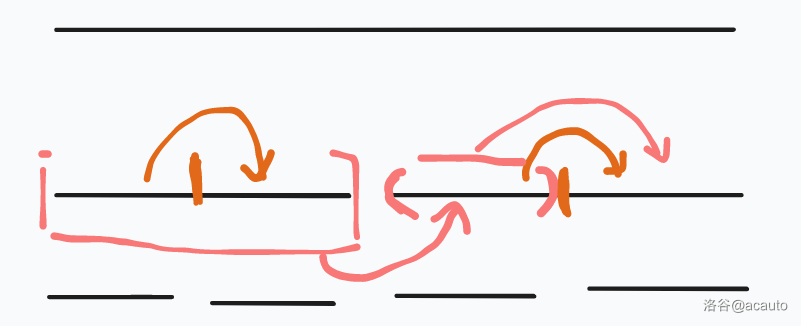
因为如果我们按平常的做法，其实是左右各自贡献，如下图中橙色。但这会出问题，我们更新最右边的时候用的是没有被左边更新的右端的左侧，所以错了。

粉色的顺序才应该是对的。

代码

#include <bits/stdc++.h>

using namespace std;

#define int long long

#define IL inline
#define vec vector
#define bg begin
#define eb emplace_back
#define emp emplace
#define fi first
#define se second
#define mkp make_pair
#define lb lower_bound
#define ub upper_bound
using ubt = long long;
using uubt = unsigned long long;
using dub = double;
using pii = pair<int, int>;
using puu = pair<ubt, ubt>;

IL void ckx(int &x, const int &y) { (x < y) && (x = y); }
IL void ckm(int &x, const int &y) { (x > y) && (x = y); }

template <typename T = int>
IL T _R() {
  T s = 0, w = 1;
  char c = getchar();
  while (!isdigit(c)) w = c == '-' ? -1 : 1, c = getchar();
  while (isdigit(c)) s = s * 10 + c - 48, c = getchar();
  return s * w;
}

const int inf = 1e18;

const int N = 1e5;
const int maxN = N + 3;

int n;
int f[maxN], id[maxN], fid[maxN];
int sot[maxN];

struct node {
  int x, y, t;
  int A;

  int k1, k2;
  IL void init() {
    k1 = -x + sot[y] - t;
    k2 = x + sot[y] - t;
  }

  IL friend bool operator < (const node &A, const node &B) {
    if (A.k2 != B.k2) return A.k2 > B.k2;
    if (A.k1 != B.k1) return A.k1 > B.k1;
    if (A.y != B.y) return A.y < B.y;
    if (A.t != B.t) return A.t < B.t;
    assert(false);
  }
  IL friend bool operator <= (const node &A, const node &B) {
    return !(B < A);
  }
} a[maxN];

IL bool cmp(int i, int j) { return a[i] < a[j]; }

struct BIT {
  int t[maxN];
  IL void ins(int x, int b) {
    for (; x <= n + 1; x += x & -x) ckx(t[x], b);
  }
  IL int ask(int x) {
    int res = -inf;
    for (; x > 0; x -= x & -x) ckx(res, t[x]);
    return res;
  }
  IL void clr(int x) {
    for (; x <= n + 1; x += x & -x) t[x] = -inf;
  }
  BIT() { memset(t, ~0x3f, sizeof(t)); }
} T;

void cdq(int l, int r) {
  if (l == r) return;
  int mid = (l + r) >> 1;
  cdq(l, mid);

  for (int i = mid + 1; i <= r; i++) fid[i] = id[i];
  sort(fid + mid + 1, fid + r + 1, cmp);
  int t1 = l, t2 = mid + 1;
  while (t1 <= mid && t2 <= r) {
    if (a[id[t1]] <= a[fid[t2]]) {
      T.ins(a[id[t1]].y, f[id[t1]]);
      t1++;
    } else {
      ckx(f[fid[t2]], T.ask(a[fid[t2]].y) + a[fid[t2]].A);
      t2++;
    }
  }
  while (t2 <= r)
    ckx(f[fid[t2]], T.ask(a[fid[t2]].y) + a[fid[t2]].A),
    t2++;
  for (int i = l; i <= mid; i++) T.clr(a[id[i]].y);

  cdq(mid + 1, r);

  stable_sort(id + l, id + r + 1, cmp);
}

signed main() {
  n = _R();
  for (int i = 1; i <= n; i++) {
    a[i].t = _R(), a[i].x = _R(), a[i].y = _R(), a[i].A = _R();
    sot[i] = a[i].y;
  }

  sot[n + 1] = 0;
  sort(sot + 1, sot + n + 2);
  for (int i = 0; i <= n; i++)
    a[i].y = lb(sot + 1, sot + n + 2, a[i].y) - sot;

  for (int i = 0; i <= n; i++)
    a[i].init();

  sort(a, a + n + 1, [&](const auto &A, const auto &B) {
    if (A.k1 != B.k1) return A.k1 > B.k1;
    if (A.k2 != B.k2) return A.k2 > B.k2;
    if (A.y != B.y) return A.y < B.y;
    if (A.t != B.t) return A.t < B.t;
    assert(false);
  });
  memset(f, ~0x3f, sizeof(f));
  f[0] = 0;
  for (int i = 0; i <= n; i++) id[i] = i;
  cdq(0, n);

  int ans = 0;
  for (int i = 1; i <= n; i++) ckx(ans, f[i]);
  printf("%lld\n", ans);
}