autograd实现线性回归

In [1]:
import torch as t
from torch.autograd import Variable as V
from matplotlib import pyplot as plt
from IPython import display
In [2]:
# 为了在不同计算机上运行时下面输出的结果一致,设置随机数种子
t.manual_seed(1000)
def get_fake_data(batch_size=8):
"""
//产生随机数:y = x*2 + 3,加上噪声
"""
x = t.rand(batch_size, 1) * 20
y = x * 2 + (1 + t.randn(batch_size, 1)) * 3
return x , y
In [3]:
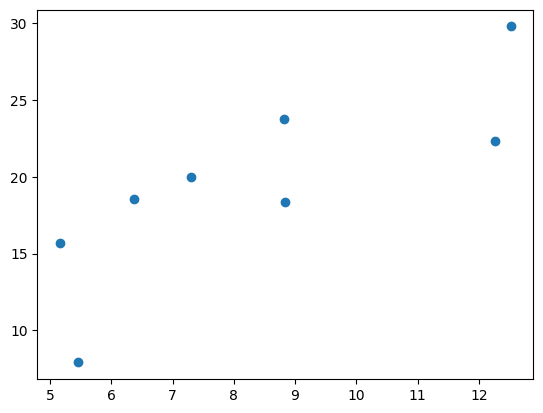
# 查看x-y的分布情况
x, y = get_fake_data()
plt.scatter(x.squeeze().numpy(), y.squeeze().numpy())
Out[3]:
<matplotlib.collections.PathCollection at 0x24972bf5508>

In [4]:
# 初始化随机参数
w = V(t.rand(1, 1), requires_grad=True)
b = V(t.zeros(1, 1), requires_grad=True)
# 设置学习率
lr = 0.001
In [5]:
for ii in range(2000):
x, y = get_fake_data()
x, y = V(x), V(y)
# forward:计算loss
y_pred = x.mm(w) + b.expand_as(y)
loss = 0.5 * (y_pred - y) ** 2
loss = loss.sum()
# backward:自动计算梯度
loss.backward()
# 更新参数
w.data.sub_(lr * w.grad.data)
b.data.sub_(lr * b.grad.data)
# 梯度清零
w.grad.data.zero_()
b.grad.data.zero_()
if ii%2000 == 0:
# 画图
display.clear_output(wait=True)
x = t.arange(0, 20).view(-1, 1)
y = x.mm(w.data.long()) + b.data.expand_as(x)
# predicted
plt.plot(x.numpy(), y.numpy())
x2, y2 = get_fake_data(batch_size=20)
# true data
plt.scatter(x2.numpy(), y2.numpy())
plt.xlim(0, 20)
plt.ylim(0, 41)
plt.show()
plt.pause(0.5)
print(w.item(), b.item())

2.054152727127075 3.0143353939056396


 浙公网安备 33010602011771号
浙公网安备 33010602011771号