线段树

推荐博客 ：http://www.cnblogs.com/TheRoadToTheGold/p/6254255.html

 

一、基本概念

1、线段树是一棵二叉搜索树，它储存的是一个区间的信息。

2、每个节点以结构体的方式存储，结构体包含以下几个信息：

     区间左端点、右端点；（这两者必有）

     这个区间要维护的信息（事实际情况而定，数目不等）。

3、线段树的基本思想：二分。

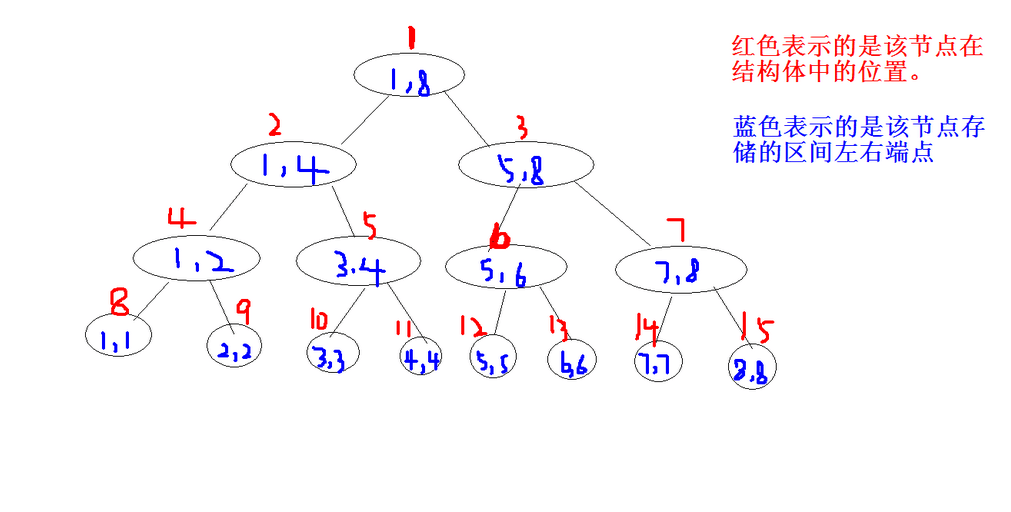
4、线段树一般结构如图所示：

　　

线段树的基本操作 ：

1 . 节点的结构

 

struct node
{
    int l, r;
    int w, f;
}tree[eps]

 

 2. 建树

void build(int l, int r, int k){
    tree[k].l = l;
    tree[k].r = r;
    if (tree[k].l == tree[k].r) {
        scanf("%d", &tree[k].w);
        return;
    }
    int m = (tree[k].l + tree[k].r) / 2;
    build(l, m, 2*k);
    build(m+1, r, 2*k+1);
    tree[k].w = tree[k].l + tree[k].r;
}

 3 . 懒标记下传操作

void down(int k){
    tree[2*k].f += tree[k].f;
    tree[2*k+1].f += tree[k].f;
    tree[2*k].w += (tree[2*k].r - tree[2*k].l + 1)*tree[k].f;
    tree[2*k+1].w += (tree[2*k+1].r - tree[2*k+1].l + 1)*tree[k].f;
    tree[k].f = 0;
}

 4 .单点查询

void ask(int k){
    if (tree[k].l == tree[k].r) {
        ans = tree[k].w;
        return;
    }
    if (tree[k].f) down(k);
    int m = (tree[k].l + tree[k].r) >> 1;
    if (x <= m) ask(2*k);
    else ask(2*k+1);
}

 5 . 单点修改

void add(int k){
    if (tree[k].l == tree[k].r){
        tree[k].w += y;
        return;
    }
    if (tree[k].f) down(k);
    int m = (tree[k].l + tree[k].r) >> 1;
    if (x <= m) add(2*k);
    else add(2*k+1);
    tree[k].w = tree[2*k].w + tree[2*k+1].w;
}

 6 . 区间查询

void sum(int k){
    if (a >= tree[k].l && b <= tree[k].r){
        ans += tree[k].w;
        return;
    }
    if (tree[k].f) down(k);
    int m = (tree[k].l + tree[k].r) >> 1;
    if (a <= m) sum(2*k);
    if (b > m) sum(2*k+1);
}

 7 . 区间修改

void change(int k){
    if (a >= tree[k].l && b <= tree[k].r){
        tree[k].w += (tree[k].r - tree[k].l + 1)*x;
        tree[k].f += x;
        return;        
    }
    if (tree[k].f) down(k);
    int m = (tree[k].l + tree[k].r) >> 1;
    if (a <= m) change(2*k);
    if (b > m) change(2*k+1);
    tree[k].w = tree[2*k].w + tree[2*k+1].w;
}

 8 . 区间替换的懒标记下传

void down(int k, int m){
    lazy[k<<1] = lazy[k<<1|1] = lazy[k];
    sum[k<<1] = (m - (m>>1)) * lazy[k];
    sum[k<<1|1] = (m >> 1) * lazy[k];
    lazy[k] = 0;
}

 9 .区间替换的代码

void change(int l, int r, int k, int pt){
    if (x <= l && r <= y){
        lazy[k] = pt;
        sum[k] = (r - l + 1) * pt;
        return;
    }
    if (lazy[k]) down(k, r - l + 1);
    int m = (l + r) >> 1;
    if (x <= m) change(lson, pt);
    if (y > m) change(rson, pt);
    sum[k] = sum[k<<1] + sum[k<<1|1];
}