Tarjan学习笔记
Tarjan
Tarjan算法是图论中非常常用的算法之一,能解决强连通分量,双连通分量,割点和桥,求最近公共祖先(LCA)等问题。
Tarjan 算法是基于深度优先搜索的算法,用于求解图的连通性问题。
割点
如果从图中删除节点 \(x\) 以及所有与 \(x\) 关联的边之后,图将被分成两个或两个以上的不相连的子图,那么称 \(x\) 为图的割点。
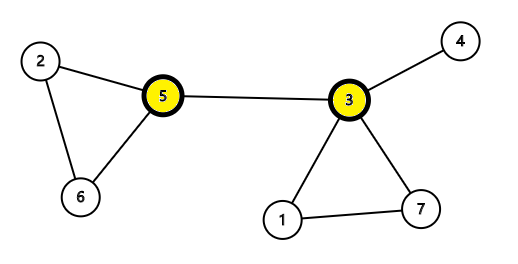
如3、5就是图的割点
桥/割边
如果从图中删除边 \(e\) 之后,图将分裂成两个不相连的子图,那么称 \(e\) 为图的桥/割边。
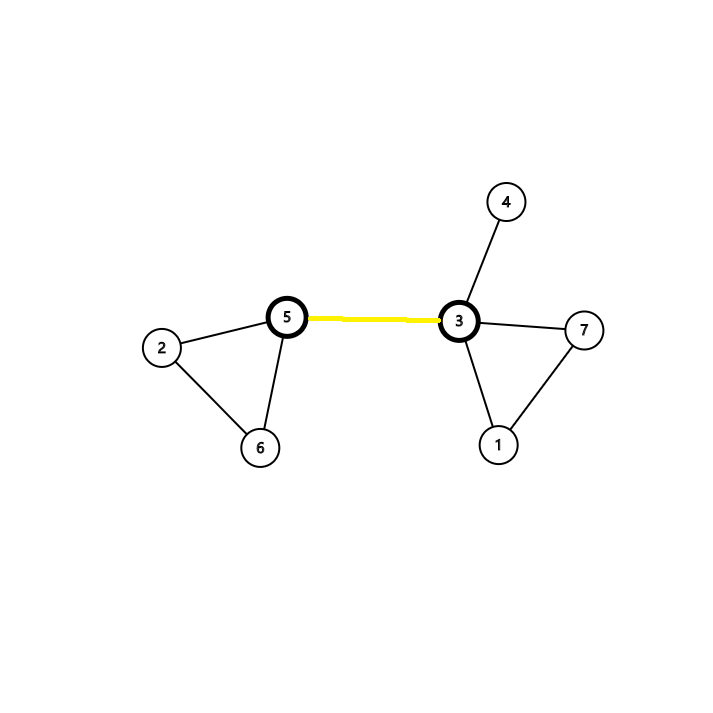
如图中边 \((3,5)\) 就是图的割边
实现
几个定义
强连通分量 :
对于一个分量,若任意两个点相通,则称为强连通分量。
树边 :
对于一个图的dfs树,它的树边便是此图的树边。
返祖边 :
对于一个图的dfs树,可以使得儿子节点返回到它的祖先的边为返祖边。
横插边 :
对于一个图的dfs树,可以使得一个节点到达另一个节点且它们互不是祖先的边为横插边。
连通
连通:无向图中,从任意点 \(i\) 可到达任一点 \(j\) 。
强连通:有向图中,从任意点 \(i\) 可到达任一点 \(j\)。
弱连通:把有向图看作无向图时,从任意点i可到达任一点 \(j\)。
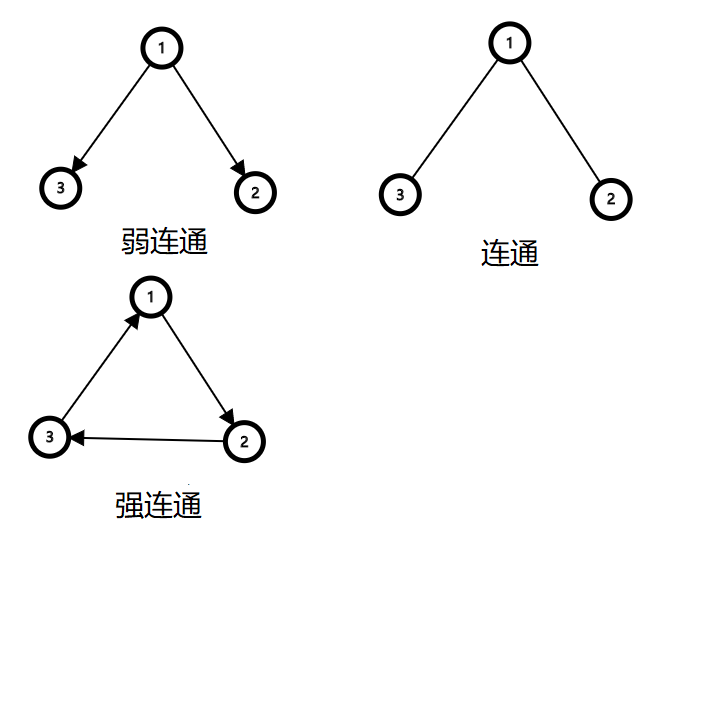
强连通分量
整个图并不是强连通的,但是在某些局部区域符合强连通的要求,如下图,整张图不算是强连通,但局部还是能满足强连通条件的。
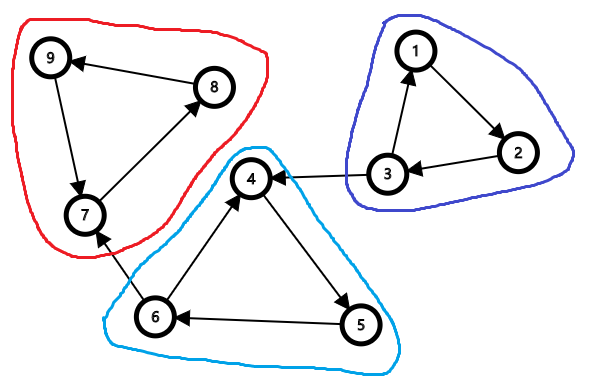
时间戳
时间戳是用来标记图中每个节点在进行dfs时被访问的顺序,可以理解成一个由小到大的序号(类似于dfs序)。
搜索树
在无向图中,以某一个节点 \(x\) 出发进行dfs,每一个节点只访问一次,所有被访问过的节点和边构成一棵树,称之为“无向连通图的搜索树”。
追溯值
追溯值用来表示从当前节点 \(x\) 能够访问到的所有节点中,时间戳最小的值。
能够访问到的节点其需要满足下面的条件之一:
- 以 \(x\) 为根的搜索树的所有节点。
- 通过一条非搜索树上的边,能够到达搜索树的所有节点。
代码
dfn:第 \(i\) 个节点的时间戳。
low:第 \(i\) 个节点最多经过一条返祖边所能到达的最小时间戳。
s:一个栈,用来储存当前还未确定但已经扩展过的点。
b:第 \(i\) 个节点是否遍历过。
ans:答案计数。
low 值与 dfn 值判断:
-
如果一个节点的
low值小于dfn值,那么就说明它或者它的子孙节点有边连到自己上方的节点。 -
如果一个节点的
low值等于dfn值,则说明其下方的节点不能走到其上方节点,那么该节点就是一个强连通分量在搜索树中的根。 -
但是 \(u\) 的子孙节点就未必和 \(u\) 处于同一个强连通分量,用栈存储即可。
void tarjan(int 当前点){
这个点的low=dfn=时间戳;
...
for(这个点连接的所有边){
if(目标点没有被访问过){
tarjan(目标点);
更新当前点的low;
...
}else if(目标点被访问过){
更新当前点的low;
...
}
}
...
}
int dfn[100010],low[100010];
int n,m,num=0,ans=0;
vector<int>v[100010];
stack<int>s;
void tarjan(int u){
dfn[u]=low[u]=++num;
...
for(int i=0;i<v[u].size();i++) {
int nn=v[u][i];
if(!dfn[nn]){
tarjan(nn);
low[u]=min(low[u],low[nn]);
...
}else if(...){
low[u]=min(low[u],dfn[nn]);
...
}
}
...
}
调用:
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i),sum=max(sum,ans);//最大强连通分量sum
LCA code
\(O(n+m)\)
并查集维护祖先。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,s;
struct ask{
int a,b;
};
vector<ask>quer[1000100];
vector<int>v[1000100];
int fa[1000001],k[1000001],d[10000001],ans[10000001];
int find(int x){
if(fa[x]==x)return x;
else return fa[x]=find(fa[x]);
}
void tarjan(int x){
k[x]=1;
for(auto i:v[x]){
if(k[i])continue;
d[i]=d[x]+1;
tarjan(i);
fa[i]=x;
}
for(int i=0;i<quer[x].size();i++){
int y=quer[x][i].a,id=quer[x][i].b;
if(k[y]==2){
int lca=find(y);
ans[id]=lca;
}
}
k[x]=2;
}
signed main(){
cin>>n>>m>>s;
for(int i=0;i<=n;i++)fa[i]=i;
for(int i=1;i<n;i++){
int uu,vv;
cin>>uu>>vv;
v[uu].push_back(vv);
v[vv].push_back(uu);
}
for(int i=1;i<=m;i++){
int uu,vv;
cin>>uu>>vv;
if(uu==vv)ans[i]=uu;
quer[uu].push_back(ask{vv,i});
quer[vv].push_back(ask{uu,i});
}
tarjan(s);
for(int i=1;i<=m;i++){
cout<<ans[i]<<endl;
}
return 0;
}
强连通分量code
用一个栈维护强连通部分+染色
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,num,cnt,ans;
stack<int>s;
vector<int>v[1000100];
int dfn[100010],low[100010],b[100010];
int color[100010],cols=0,cl[100010];
void paint(){
color[s.top()]=cols;
cl[cols]++;
b[s.top()]=0;
}
void tarjan(int u){
num++;
dfn[u]=low[u]=num;
s.push(u);
b[u]=1;
for(int i=0;i<v[u].size();i++) {
int nn=v[u][i];
if(!dfn[nn]){
tarjan(nn);
low[u]=min(low[u],low[nn]);
}else if(b[nn]){
low[u]=min(low[u],dfn[nn]);
}
}
if(low[u]==dfn[u]){
cols++;
while(!s.empty()&&s.top()!=u){
paint();
s.pop();
}
paint();
s.pop();
}
}
signed main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int uu,vv;
cin>>uu>>vv;
v[uu].push_back(vv);
}
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
for(int i=1;i<=cols;i++){
if(cl[i]>1)ans++;
//cout<<cl[i]<<" ";
}
cout<<ans<<endl;
return 0;
}
割点/割边(桥)
判定
割点:如果一个点 \(u\) 为割点,那么有两种情况:
-
\(u\) 为树根,且有超过一个子树。
-
\(u\) 不为树根,且满足存在 \((u, v)\) 为树枝边,使得 \(dfn(u) \le low(v)\)。
桥:如果一条无向边 $ (u, v) $ 是桥,当且仅当 $(u, v) $ 为树枝边,且满足 \(dfn[u] < low[v]\) (前提是这条边不存在重边)。
求割点code
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,root,num,cnt,ans;
vector<int>v[1000100];
int dfn[100010],low[100010],st[100010],b[100010];
void tarjan(int x){
int son=0;
dfn[x]=low[x]=++num;
s.push(x);
b[x]=1;
for(int i=0;i<v[x].size();i++) {
int nn=v[x][i];
if(!dfn[nn]){
tarjan(nn);
son++;
low[x]=min(low[x],low[nn]);
if(low[nn]>=dfn[x]&&x!=root&&!st[x]){
cnt++;st[x]=1;
}
}else if(b[nn]){
low[x]=min(low[x],dfn[nn]);
}
}
if(son>=2&&x==root&&!st[x]){
cnt++;st[x]=1;
}
}
signed main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int uu,vv;
cin>>uu>>vv;
v[uu].push_back(vv);
v[vv].push_back(uu);
}
for(int i=1;i<=n;i++)if(!dfn[i])root=i,tarjan(i);
cout<<cnt<<endl;
for(int i=1;i<=n;i++){
if(st[i])cout<<i<<" ";
}
return 0;
}
求割边code
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,num,cnt,ans;
stack<int>s;
vector<int>v[1000100];
int dfn[100010],low[100010],b[100010];
struct edge{
int l,r;
bool operator <(const edge bb)const{
if(l==bb.l)return r<bb.r;
return l<bb.l;
}
}e[100010];
int es=0;
void tarjan(int x,int la){
dfn[x]=low[x]=++num;
b[x]=1;
for(int i=0;i<v[x].size();i++) {
int nn=v[x][i];
if(!dfn[nn]){
tarjan(nn,x);
low[x]=min(low[x],low[nn]);
if(low[nn]>dfn[x]){
if(x>nn)e[es++]=edge{nn,x};
else e[es++]=edge{x,nn};
}
}else if(nn!=la){
low[x]=min(low[x],dfn[nn]);
}
}
}
signed main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int uu,vv;
cin>>uu>>vv;
v[uu].push_back(vv);
v[vv].push_back(uu);
}
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i,0);
sort(e,e+es);
for(int i=0;i<es;i++)cout<<e[i].l<<" "<<e[i].r<<endl;
return 0;
}
缩点code
无非就是把染色那加了缩点(即删除节点 \(y\),增加 \(u\) 权值的操作)
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,num,cnt,ans;
stack<int>s;
vector<int>v[1000100];
int dfn[100010],low[100010],b[100010];
int col[100010],p[100010];
void tarjan(int u){
dfn[u]=low[u]=++num;
s.push(u);
b[u]=1;
for(int i=0;i<v[u].size();i++) {
int nn=v[u][i];
if(!dfn[nn]){
tarjan(nn);
low[u]=min(low[u],low[nn]);
}else if(b[nn]){
low[u]=min(low[u],dfn[nn]);
}
}
if(low[u]==dfn[u]){
while(!s.empty()&&s.top()!=u){
int y=s.top();
col[y]=u;
b[y]=0;
if(u==y)break;
p[u]+=p[y];
s.pop();
}
col[u]=u;
b[u]=0;
s.pop();
}
}
int ru[100010];
vector<int>nv[100010];
int dis[100010],vis[100010];
int getans(){
queue<int>q;
int tot=0;
for(int i=1;i<=n;i++)
if(col[i]==i&&!ru[i]){
q.push(i);
dis[i]=p[i];
}
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<nv[u].size();i++){
int y=nv[u][i];
dis[y]=max(dis[y],dis[u]+p[y]);
ru[y]--;
if(ru[y]==0)q.push(y);
}
}
int ans=0;
for(int i=1;i<=n;i++)ans=max(ans,dis[i]);
return ans;
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>p[i];
for(int i=1;i<=m;i++){
int uu,vv;
cin>>uu>>vv;
v[uu].push_back(vv);
}
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
for(int i=1;i<=n;i++){
for(auto k:v[i]){
int x=col[i],y=col[k];
if(x!=y){
nv[x].push_back(y);
ru[y]++;
}
}
}
cout<<getans()<<endl;
return 0;
}
双连通分量
点双连通分量code
点双连通:在一个无向图中,若任意两点间至少存在两条“点不重复”的路径。
点双连通分量:一个子图满足点双连通且在图 \(G\) 中是极大联通子图
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,num,cnt,ans;
vector<int>anss[5000101];
stack<int>s;
vector<int>v[5000100];
int dfn[5000010],low[5000010],b[5000010];
int ru[5000010];
void tarjan(int x,int fa){
int son=0;
dfn[x]=low[x]=++num;
s.push(x);
for(int i=0;i<v[x].size();i++) {
int nn=v[x][i];
if(!dfn[nn]){
tarjan(nn,x);
son++;
low[x]=min(low[x],low[nn]);
if(low[nn]>=dfn[x]){
cnt++;
int p;
do{
p=s.top();
s.pop();
anss[cnt].push_back(p);
}while(p!=nn);
anss[cnt].push_back(x);
}
}else if(nn!=fa){
low[x]=min(low[x],dfn[nn]);
}
}
if(!son&&!fa){
anss[++cnt].push_back(x);
}
}
signed main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int uu,vv;
cin>>uu>>vv;
if(uu==vv)continue;
ru[vv]++,ru[uu]++;
v[uu].push_back(vv);
v[vv].push_back(uu);
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
while(!s.empty())s.pop();
tarjan(i,0);
}
}
cout<<cnt<<endl;
for(int i=1;i<=cnt;i++){
cout<<anss[i].size()<<" ";
for(auto j:anss[i])cout<<j<<" ";
cout<<endl;
}
return 0;
}
边双连通分量code
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,num,ans;
vector<int>v[1000100];
int dfn[1000010],low[1000010],b[1000010];
int vs=0,cnt=1,head[2000005];
bool vis[2000005];
struct edge{
int to,next,q;
}e[5000010];
void add(int u,int v){
e[++cnt].to=v;
e[cnt].q=0;
e[cnt].next=head[u];
head[u]=cnt;
}
void tarjan(int x,int la){
dfn[x]=low[x]=++num;
for(int i=head[x];i;i=e[i].next){
int nn=e[i].to;
if(!dfn[nn]){
tarjan(nn,x);
low[x]=min(low[x],low[nn]);
if(low[nn]>dfn[x]){
e[i].q=e[i^1].q=1;
}
}else if(nn!=la){
low[x]=min(low[x],dfn[nn]);
}
}
}
void dfs(int x){
v[vs].push_back(x);
b[x]=1;
for(int i=head[x];i;i=e[i].next){
if(!b[e[i].to]&&!e[i].q)dfs(e[i].to);
}
}
signed main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int uu,vv;
cin>>uu>>vv;
add(uu,vv);
add(vv,uu);
}
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i,0);
for(int i=1;i<=n;i++){
if(!b[i])vs++,dfs(i);
}
cout<<vs<<endl;
for(int i=1;i<=vs;i++){
cout<<v[i].size()<<" ";
for(auto j:v[i])cout<<j<<" ";
cout<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号