最小生成树学习笔记

---

Prim算法

prim算法基本思想：基于点的解决方式

1. 先随便选择一个点s作为起点，把其他所有点设为未添加节点，再设一dis数组，代表每个
   节点到最小生成树最近点的距离，易得一开始只有dis[s]=0，其他均为∞。
2. 每轮找到dis值最小且未添加过的节点加入生成树中，且使用这个节点的邻边去更新它的邻
   点的dis值，如更新点为u，u->v有一条长度为x的边，则我们可以更新dis[v]为min(dis[v],x)。
3. 重复执行操作②，直到所有点全部被添加。

伪代码

int prim(){
	d[1]=0; mst=0;
	for(each 除1以外的点v)d[v]=∞;
	for(i=1~n){
		找到未激活且d值最小的点u。
		if(找不到u) return -1;
		else mst+=d[u],u设为已激活;
		for (each u的后继点v)
			d[v]=min(d[v],G[u][v]);
	}
	return mst;
}

代码

struct point{
	int d,s;
	bool operator < (const point &a) const {
	    return s > a.s;
	}
};
vector<point>v[50100];
int prim(){
	int ans=0;
	for(int i=1;i<=n;i++)dis[i]=1e9;
	priority_queue<point>q;
	dis[1]=0;
	q.push(point{1,0});
	while(!q.empty()&&c<n){
		int u=q.top().d;
		q.pop();
		if(!b[u]){
			c++;
			b[u]=1;
			for(int i=0;i<v[u].size();i++){
				int d=v[u][i].d,s=v[u][i].s;
				//cout<<d<<" "<<s<<' '<<dis[d]<<endl;
				if(!b[d]&&dis[d]>s){
					dis[d]=s;
					q.push(point{d,dis[d]});
				}
			}
			ans+=dis[u];
		}
	}
	//cout<<c<<endl;
	if(c==n)return ans;
	else return -1;
}

Kruskal

考虑一种贪心的思想：从小到大加边

1. 初始化。将所有边都按权值从小到大排序，将每个节点集合号都初始化为自身编号。

2. 按排序后的顺序选择权值最小的边 $（u,v）$。

3. 如果节点 $u$ 和 $v$ 属于两个不同的连通分支，则将边 $(u,v)$ 加入边集 $TE$ 中，并将两个连通分支合并。

4. 如果选取的边数小于 $n-1$ ,则转向步骤2，否则算法结束。

图解

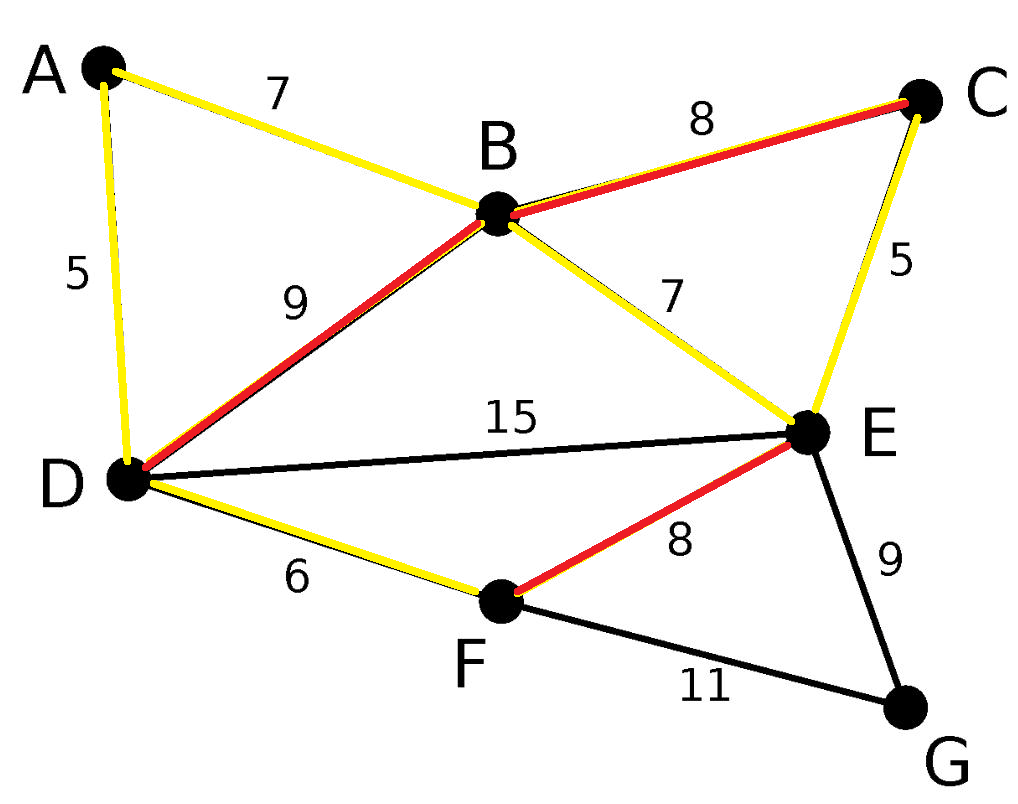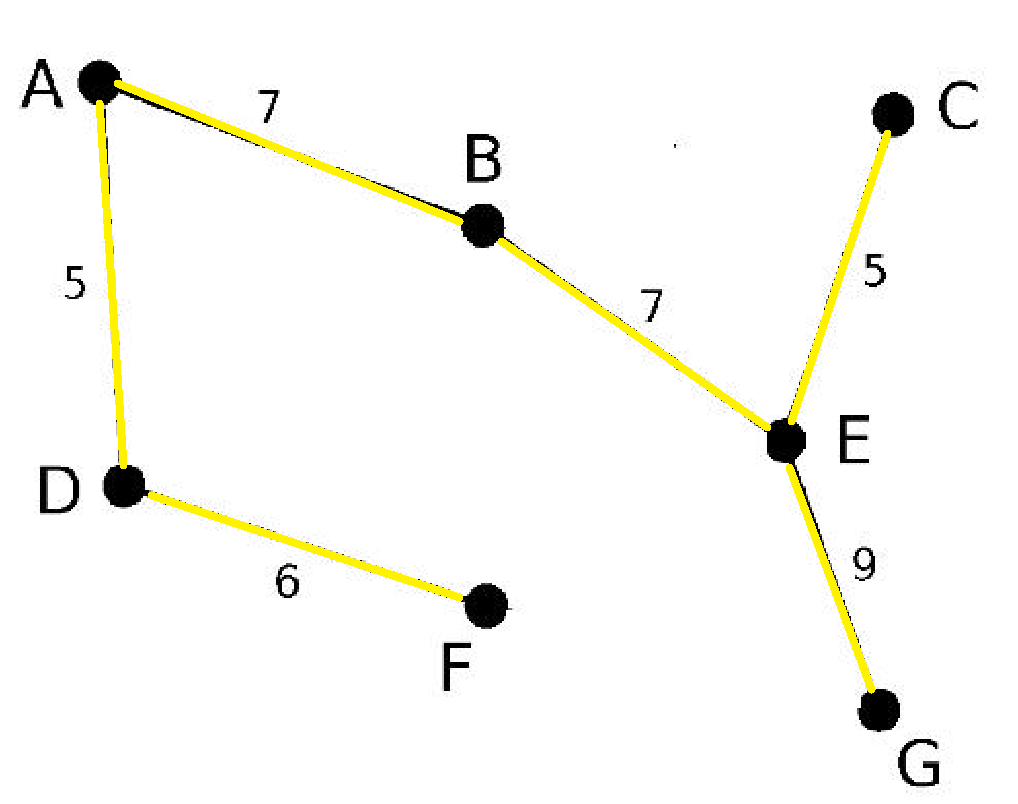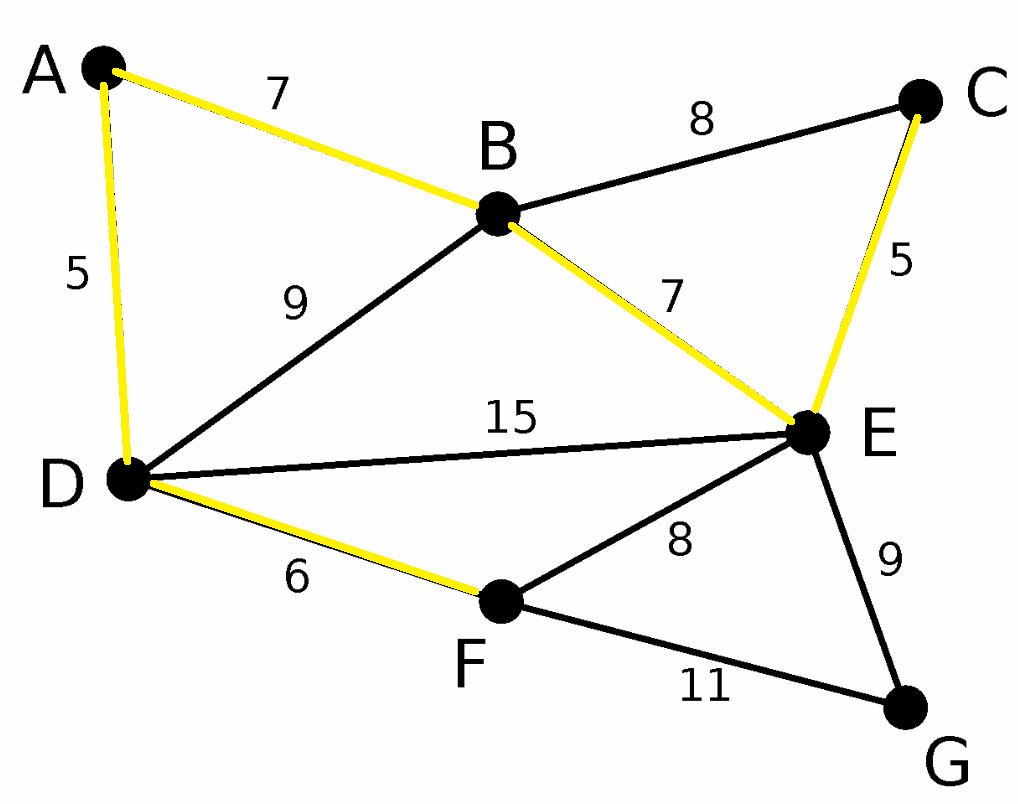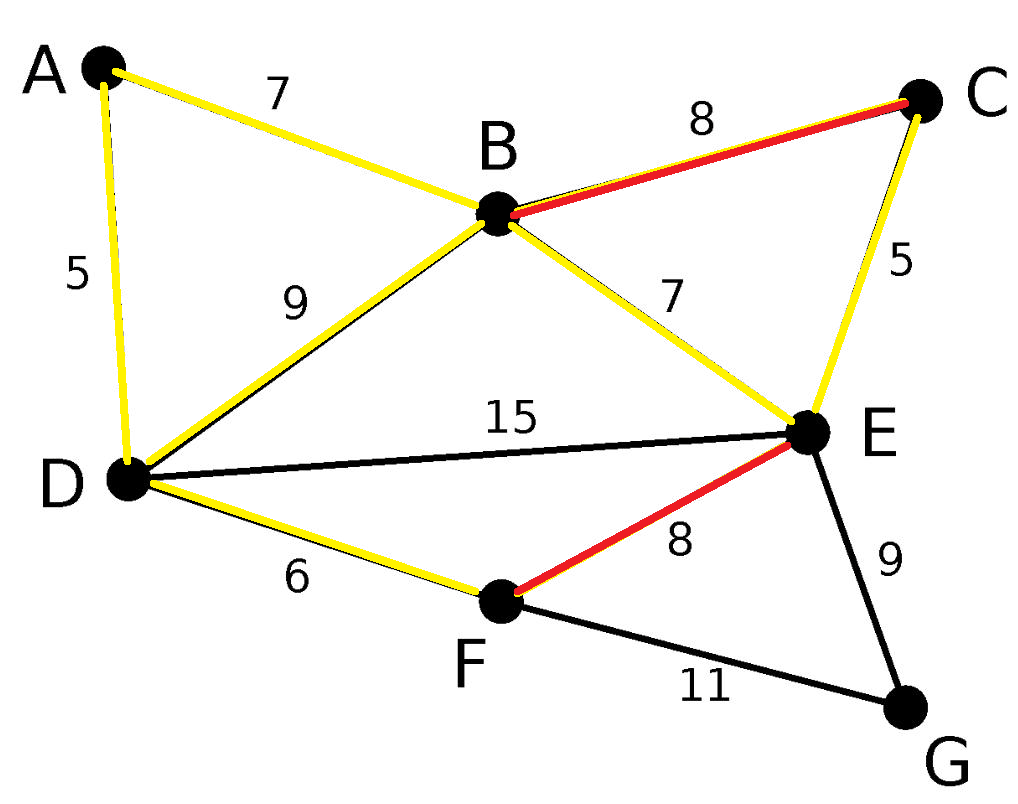
结果：

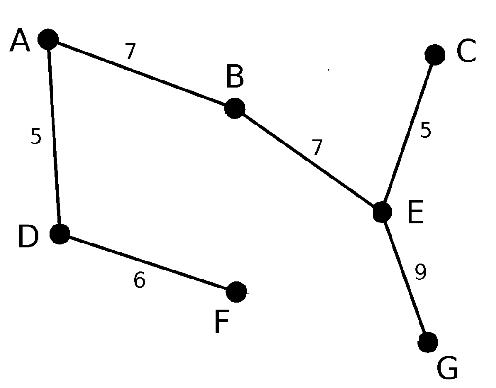
伪代码

int kruskal(){
	给边集按权值w排序。
	mst=0；
	for(each 边集中的边(u,v,w)){
		if(u和v不在一个集合中){
			mst+=w;
			将u和v连起来;
		if(所有点在一个集合中)
			return mst;
		}
	}
	return -1;
}

代码

int fa[100001],n,k,m,ans,cnt;
struct edge{
	int u,v,w;
}v[201000];
bool cmp(edge x,edge y){
    return x.w<y.w;
}
int find(int x){
    while(x!=fa[x])x=fa[x]=fa[fa[x]];
    return x;
}
int kruskal(){
    sort(v,v+m,cmp);
	for(int i=0;i<=n;i++)fa[i]=i;
    for(int i=0;i<m;i++){
        int fu=find(v[i].u),fv=find(v[i].v);
        if(fu==fv)continue;
        ans+=v[i].w;
        fa[fv]=fu;
		cnt++;
        if(cnt==n-1)return ans;
    }
    return -1;
}

复杂度

kruskal:$O(mlogm)$
prim:$O(mlogn)$