4-1 自注意力机制

1、背景

到目前为止，我们network的input都是一个向量，输入可能是一个数值或者一个类别。但是假设我们需要输入的是一排向量，并且向量的个数可能会发生改变，例如文本输入等，这个时候我们要将模型的输入作为一个向量集合，并且大小各异。

2、将单词表示为向量进行输入的方法

One-hot Encoding（独热编码）：向量的长度就是世界上所有词汇的数目，用不同位的1（其余位置为0）表示一个词汇，但是它并不能区分出同类别的词汇，里面没有任何有意义的信息。如下所示：

apple = [1, 0, 0, 0, 0, …]
bag = [0, 1, 0, 0, 0, …]
cat = [0, 0, 1, 0, 0, …]
dog = [0, 0, 0, 1, 0, …]
computer = [0, 0, 0, 0, 1, …]

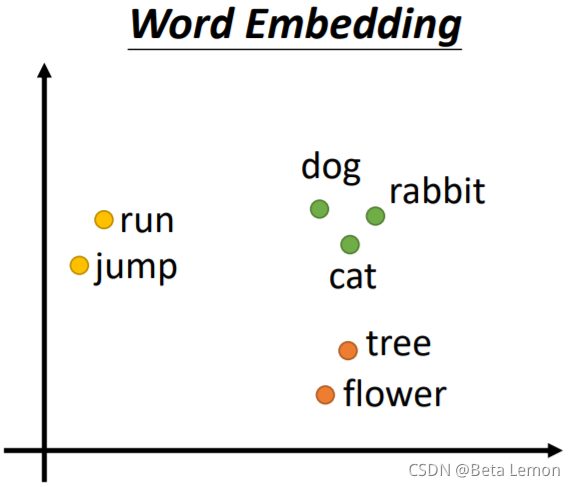
Word Embedding：给单词一个向量，这个向量有语义的信息，一个句子就是一排长度不一的向量。将Word Embedding画出来，就会发现同类的单词就会聚集，因此它能区分出类别：

3、将语音信号、图像信号也能描述为一串向量进行输入的方法

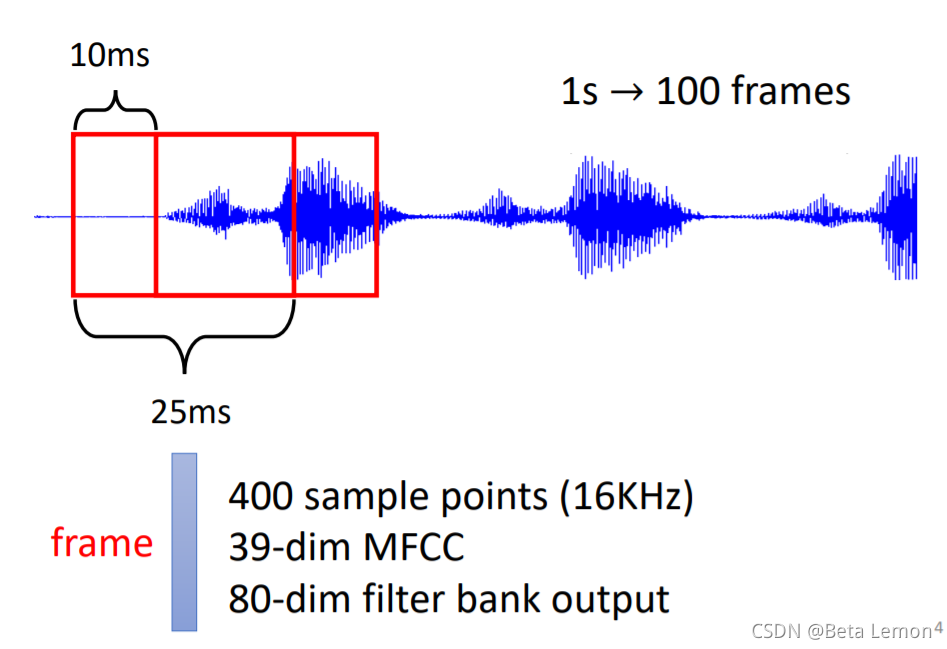
语音信号：取一段语音信号作为窗口，把其中的信息描述为一个向量（帧），滑动这个窗口就得到这段语音的所有向量

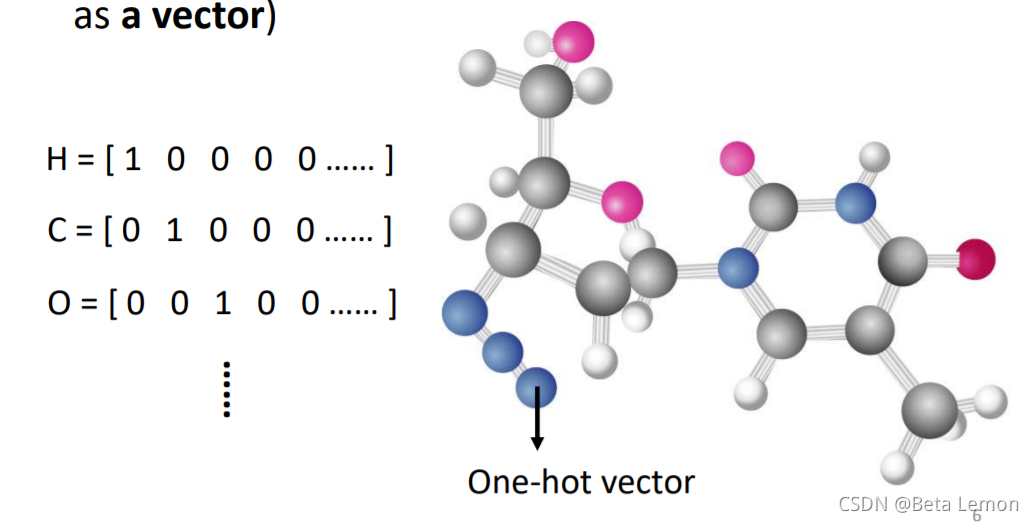
图像信号：分子上的每个原子就是一个向量（每个元素可用One-hot编码表示），分子就是一堆向量

4、模型输出的方法：有三种可能性

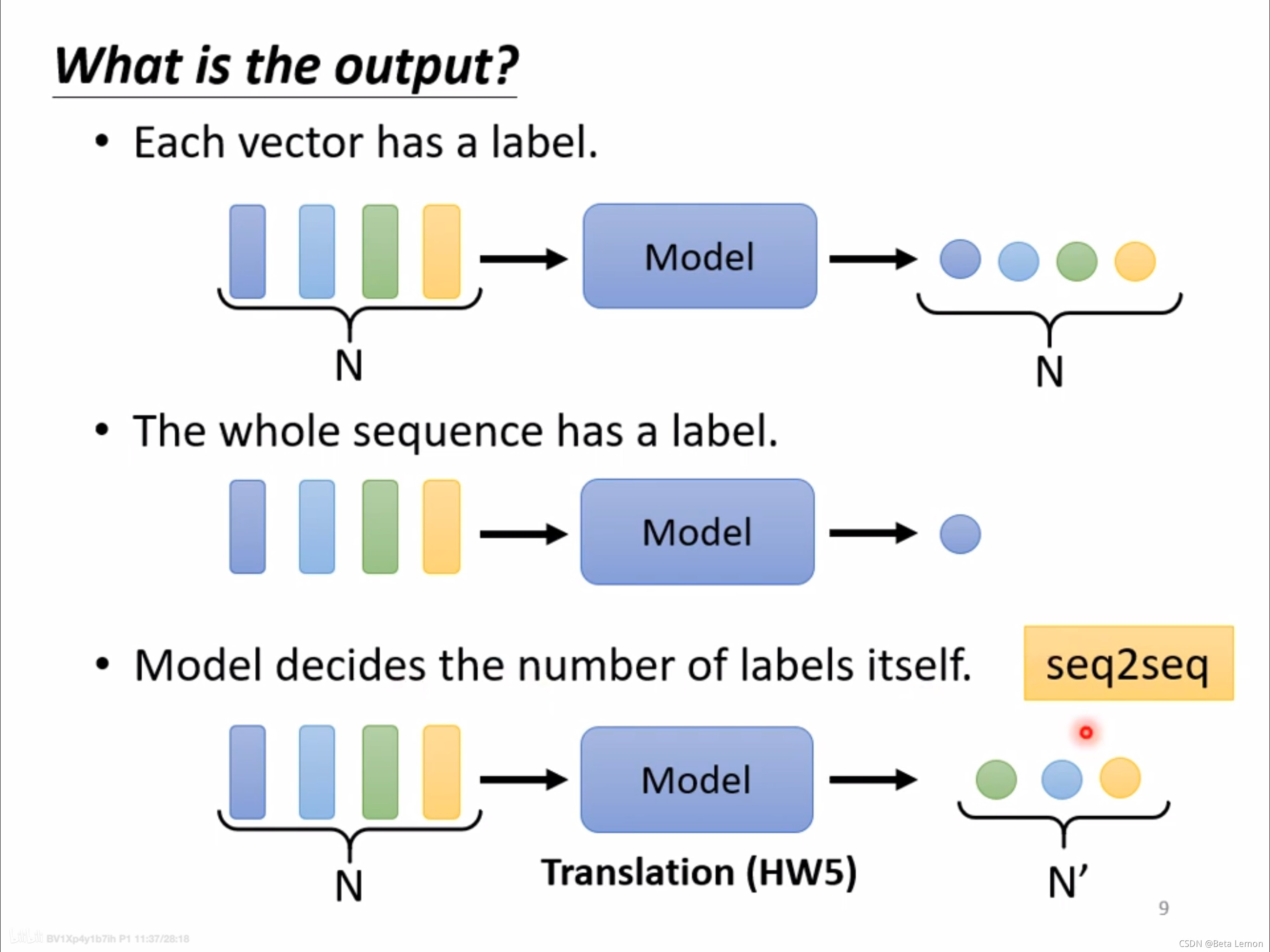
类型一：一对一（Sequence Labeling）

这是本次课的重点，其余的之后会再进行提及
每个输入向量对应一个输出标签。

• 文字处理：词性标注（每个输入的单词都输出对应的词性）。
• 语音处理：一段声音信号里面有一串向量，每个向量对应一个音标。
• 图像处理：在社交网络中，推荐某个用户商品（可能会买或者不买）。

类型二：多对一

多个输入向量对应一个输出标签。

• 语义分析：正面评价、负面评价。
• 语音识别：识别某人的音色。
• 图像：给出分子的结构，判断其亲水性。

类型三：由模型自定（seq2seq）

不知道应该输出多少个标签，机器自行决定。

• 翻译：语言A到语言B，单词字符数目不同
• 语音识别

5、序列标注 (Sequnce Labeling) 的问题——引出Self-attention

我们可以用fully conneted network解决Sequnce Labeling的问题，但是这样会有瑕疵，比如输入I saw a saw，这两个saw，对于FC（fully conneted network，全连接网络，下同）来说，是一模一样的，但是实际上它们一个是动词，一个是名词，是有区别的。这个时候我们想到考虑上下文关系来判断词性：利用滑动窗口，每个向量查看窗口中相邻的其他向量的性质。但是这样不能解决所有的问题，因为我们输入的sequence是有长有短的，如果开一个大的Window，那FCN就需要非常多的参数，不止是很难训练，而且很容易过拟合。这就引出了解决此问题的第二种方法—— Self-attention 技术。

6、Self-attention 自注意力机制

（1）设计动机：

输入可能是一个向量的序列，并且序列的长度是不确定的情况下，如果将整个序列作为一个整体，普通的模型是无法进行处理的；如果将序列中的每个向量单独交给模型处理，那么无法利用向量之间的关联性。（比如在词性标注任务中，同一个单词可能会被标注为不同的词性，但这是要结合上下文决定的，而不仅仅是单词本身。）
Self-Attention的设计动机就是处理形式为可变长度向量序列输入，且这些向量之间会有一定的关联。

（2）Self-attention

self-attention会把一整个sequence的资讯都吃进去，然后你输入几个向量，它就输出几个向量，比如图上，输入不同颜色的向量，就会输出不同颜色的向量，这里用黑色的框框，表示它不是普通的向量，是用来表示考虑了一整个sequence的向量。

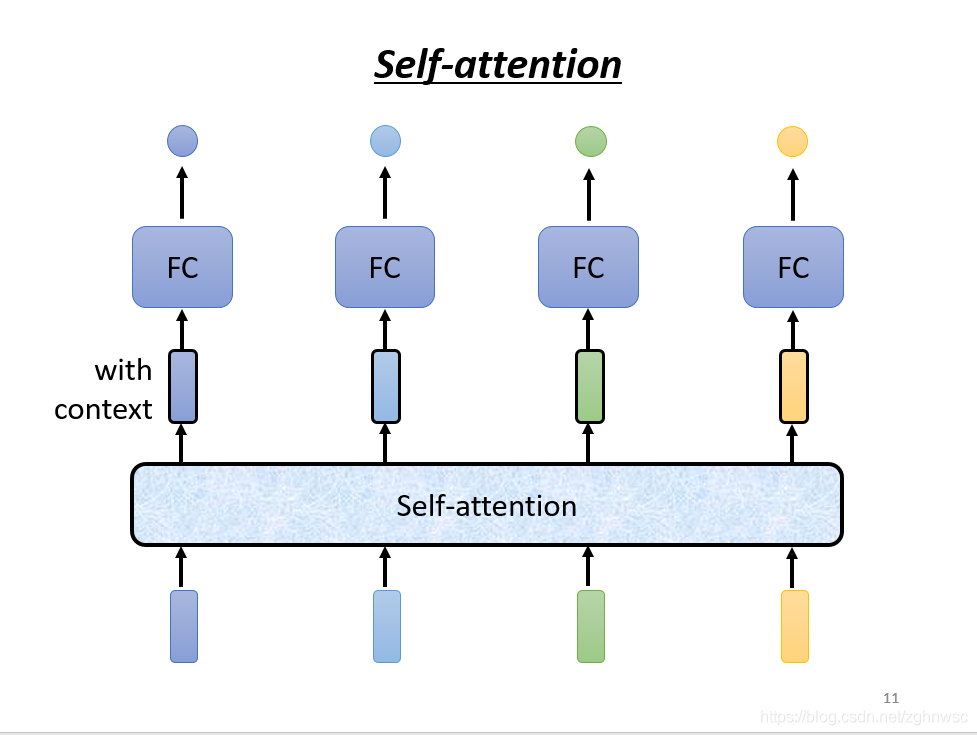
self-attention也可以和FC交替使用，用self-attention来处理整个sequence的资讯，FC来专注处理某一个位置的资讯。

（3）设计原理

需要三个向量：Query，Key，Value

以下内容均来自csdn文章如何理解 Transformer 中的 Query、Key 与 Value
self-attention 之所以取推荐系统中的 query、key 、value三个概念，就是利用了与推荐系统相似的流程。但是 self-attention 不是为了 query 去找 value，而是根据当前 query 获取 value 的加权和。这是 self-attention 的任务使然，想要为当前输入找到一个更好的加权输出，该输出要包含所有可见的输入序列信息，而注意力就是通过权重来控制。
self-attention 中这里 key 和 value 都是输入序列本身的一个变换，可能这也是 self-attention 的另外一层含义吧：自身同时作为 key 和 value。其实也非常合理，因为在推荐系统中，虽然 key 和 value 属性原始的特征空间不同，但是它们是有强关联关系的，因此他们通过一定的空间变换，是可以统一到一个特征空间中。这也是为什么self-attention 要乘以 W 的原因之一。

Self-Attention的具体设计主要包括两个部分，计算输入向量之间的相关性和根据相关性提取相关性高的信息。

• self-attention的inpu就是一串的向量，这个向量可能是整个网络的input，也可能是中间某一层的output，所以我们用a来表示它，代表它可能做过一些处理。
  这里的每一个b都是考虑了所有的a产生的，比如b1是考虑a1-a4产生的，b2是考虑a1-a4产生的。

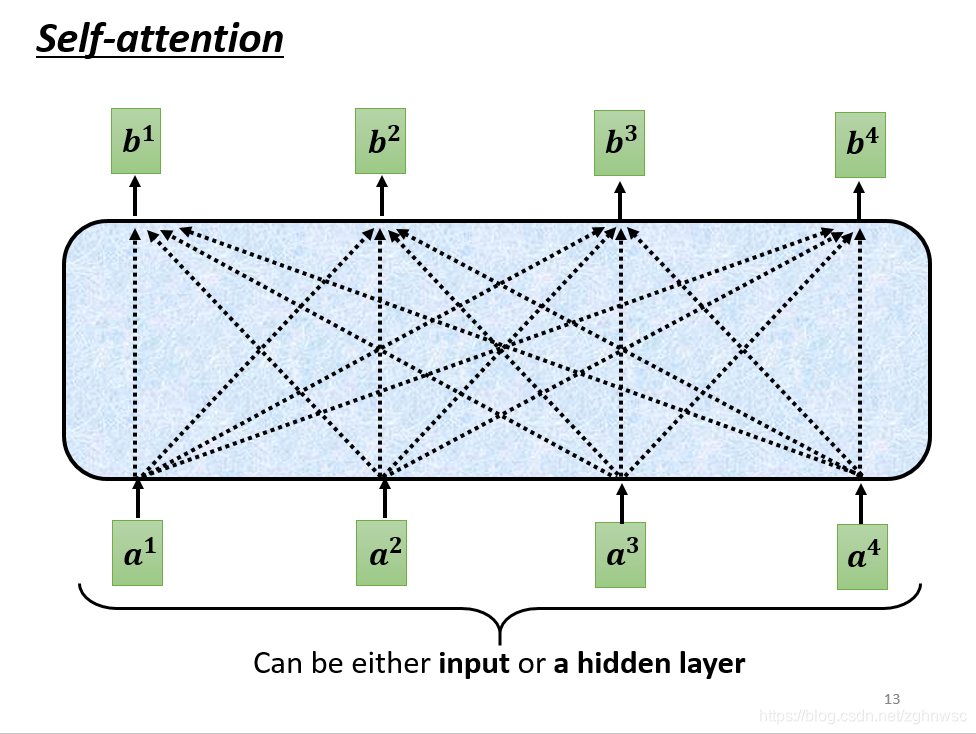
• 怎么产生b1这个向量呢？根据a1找出这个sequence里面和a1相关的其他向量，每一个向量和a1关联的程度，我们用一个数值α来表示。

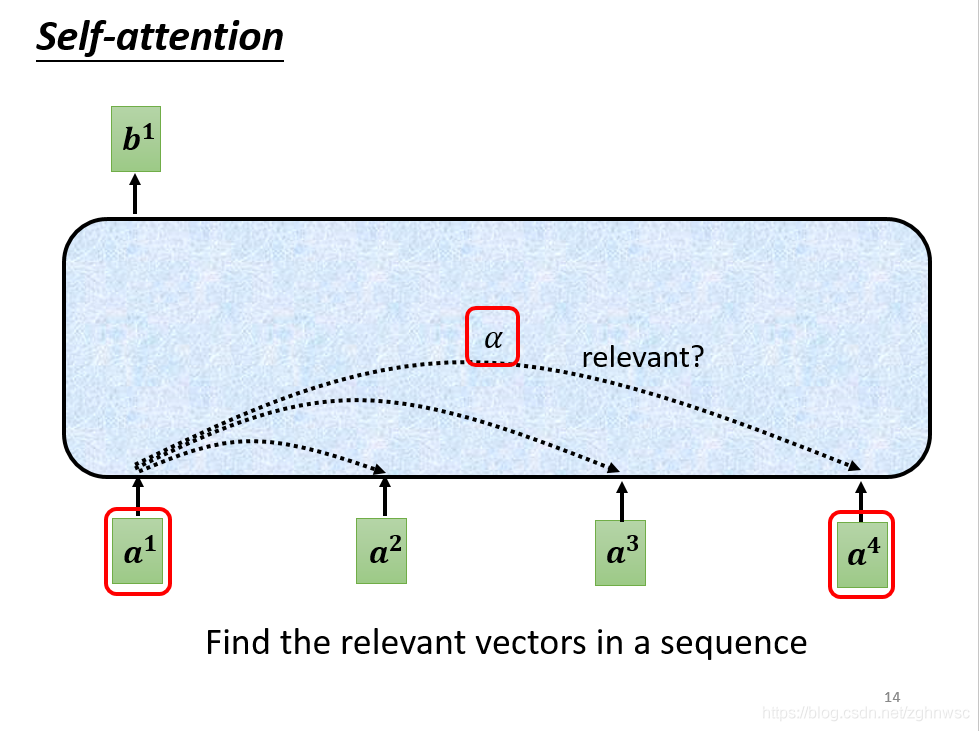
• α的产生需要一个计算attention的模组。这个模组，就是拿两个向量a1和a4作为输入，然后输出的是一个α。
  怎么计算这个数值，有各种不同的做法，比较常见的有dot-product。就是左边这个向量乘以一个Wq，右边这个向量乘以一个Wk，得到q和k，再把他们做element-wise，然后再全部加起来，得到一个scalar，这个scalar就是α。
  还有其他的方式，比如additive，就是把他们分别乘以一个矩阵，再加起来，再经过一个激活函数，最后经过一个transfor，最后得到一个α。

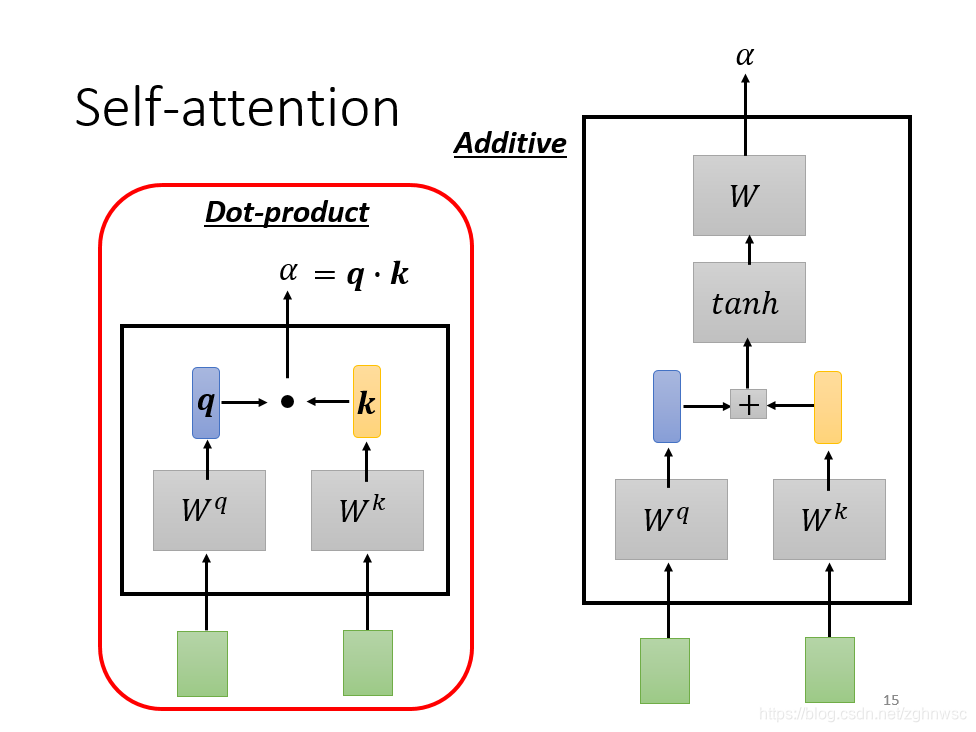
• 怎么把它套用在self-attention里面呢？
  这里就是把a1和a2、a3、a4分别去计算他们之间的关联性。就是把a1乘上Wq得到q1，叫做query。a2、a3、a4都乘以一个Wk得到一个k2，叫做key。再把q1和k2算inner-product得到α。α1，2就表示，query是1提供的，key是2提供的，就表示1和2之间的关联性。α1,2也叫做attention score，就是attention的分数。接下来就以此类推，和a3、a4计算，得到α1,3,和α1,4。实际操作中，a1也会计算和自己的关联性，就是算出来一个α1,1（目的在于简便计算，事实上算不算对于结果的影响并不大）

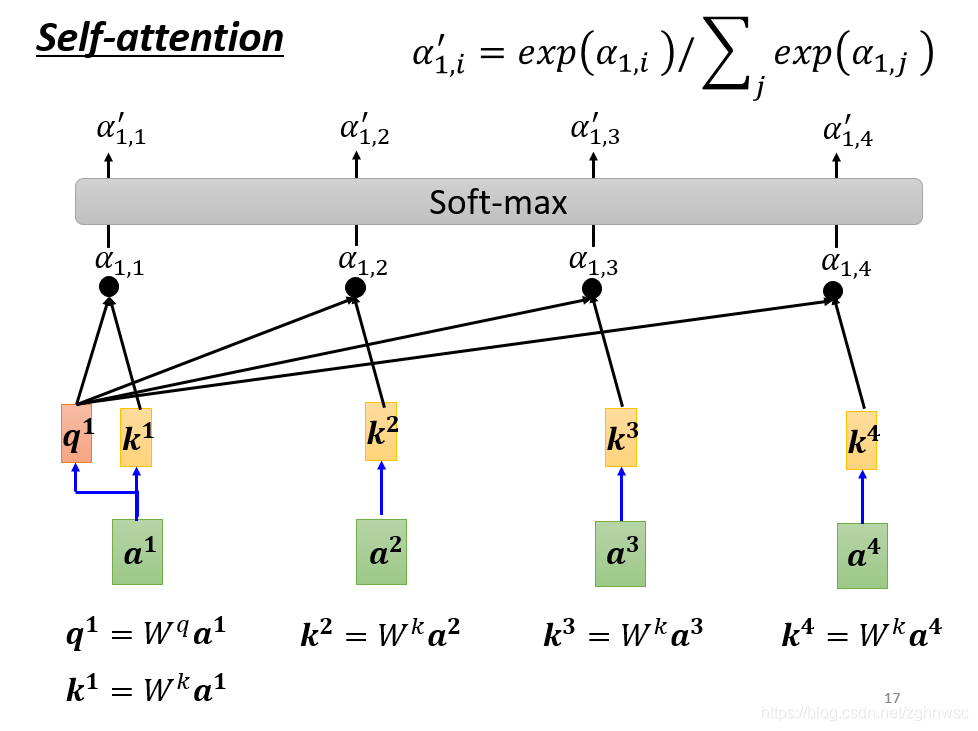
• 算完关联性之后，会做一个soft-max
  softmax就是把多个数值标准化到0~1之间，分类问题里面是根据这个可能更好的看出最后是分到哪一类里面，相当于增强最大可能的项。事实上，softmax不是必须的，也可以用ReLU等代替

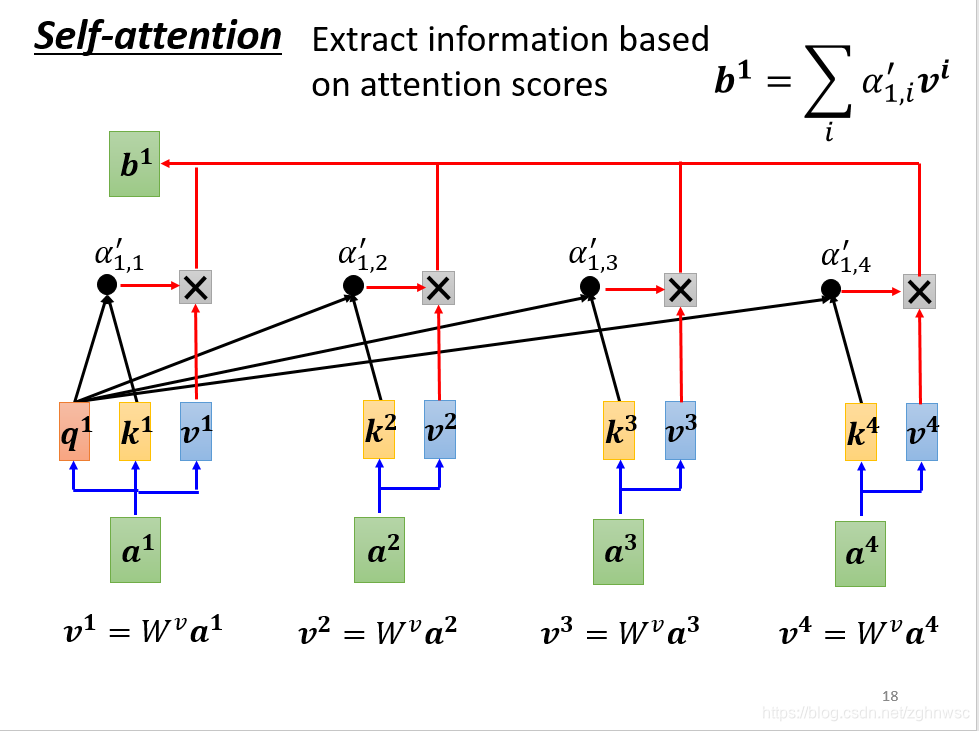
接下来我们根据这个关联性，来抽取重要的资讯。我们会把a1_{a4这里面每一个向量，乘上Wv得到一个新的向量，用v1、v2、v3、v4表示。随后把v1}v4每一个都乘上α’，然后加起来得到b。这里就是如果某一个关联性很强，比如得到的v2的值很大，那么加起来之后，这个值可能就会更加接近v2

（4）总结上述过程

• 输入矩阵I分别乘以三个W得到三个矩阵Q,K,V

• \[A=QK^{T}$$，经过处理得到注意力矩阵 \]

• 输出$$O=A^{\prime}V$$
  即:

\[\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V \]

其中，$$\sqrt{d_{k}}$$为向量的长度。

（5）注意力系数的计算

• 阶段1：根据Query和Key计算两者的相似性或者相关性
• 阶段2：对第一阶段的原始分值进 行归一化处理
• 阶段3：根据权重系数对Value进行加权求和，得到Attention Value

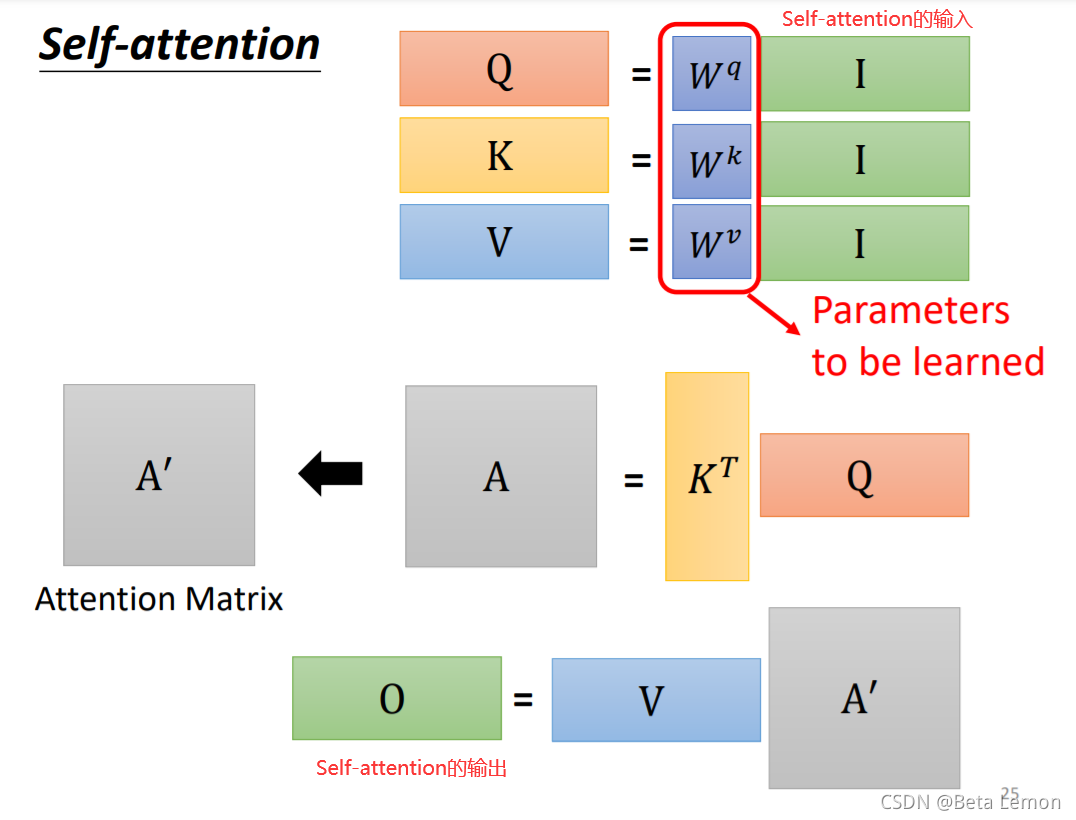
唯一要训练出的参数就是W

（6）设计原理——矩阵的层次

• 每一个a，都分别要产生不同的q，k，v。要用矩阵运算表示的话，就是每一个a都要乘上一个wq，这里我们可以把它们合起来看成是一个矩阵。就相当于矩阵I乘上一个Wq得到一个矩阵Q。k和v以此类推，只是现在把它写成了矩阵的形式

• k1和q1做inner-product，得到α1,1，同理得到α1,2和α1,3。这几步的操作，可以看做是一个矩阵的相乘。写成右上角的形式。

• 把A做一个normalization，比如做一个softmax，让每一个column里面的值，相加得1，得到一个A’。

• b就是把v拼起来，乘以一个A’，两个矩阵相乘。

• 这一连串的操作，就是矩阵的乘法。O就是这层的输出，这里只有Wq和Wk和Wv是未知的，是需要通过我们的训练资料找出来的。

7、Self-attention的进阶版——多头注意力机制 (Multi-head Self-attention)

（1）Multi-head Self-Attention的整体结构

Multi-head Self-attention与普通的Self-attention的区别在于Multi-head Self-attention会在q qq的基础上继续生成多个不同的qⁱ（k、v也是类似）。

（2）Multi-head Self-attention的设计动机

Self-attention的目的是要找相关的q qq和k kk，但是相关性的定义可能有很多种，所以可考虑设计多个q qq，不同的q qq用于寻找不同的相关性。

（3）Multi-head Self-attention与普通的Self-attention的区别

Multi-head Self-attention的每一个向量会在生成向量q qq的基础上，再乘上若干个矩阵生成多个不同的q^i,j，上图所示的情况是2个不同的q，也即两头的情况。与之相应的，向量k kk和v vv也会生成多个。
然后对每一个“头”上的向量进行与普通Self-attention相同的操作，得到每一“头”的输出b^i,j。然后可以将b^i,j拼接起来，再乘上一个矩阵得到最终的Self-Attention层的输出。

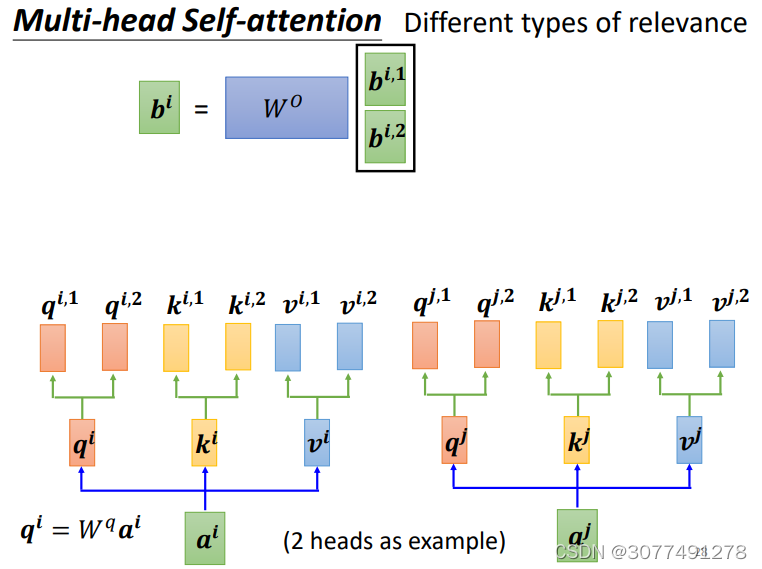
8、自注意力中的缩放

维度较大时，向量内积容易使得 SoftMax 将概率全部分配给最大值对应的 Label，其他 Label 的概率几乎为 0，反向传播时这些梯度会变得很小甚至为 0，导致无法更新参数。因此，一般会对其进行缩放，缩放值一般使用维度 dk 开根号，是因为点积的方差是 dk，缩放后点积的方差为常数 1，这样就可以避免梯度消失问题。

至于为啥最后一层为啥一般不需要缩放，因为最后输出的一般是分类结果，参数更新不需要继续传播，自然也就不会有梯度消失的问题。

9、位置编码 (Positional Encoding)

Self-attention是无法利用输入的位置信息的。因为他的计算结果取决于输入的向量相似性，所以向量在序列中的位置如果发送改变，也并不影响其结果，也就是说Self-attention并没有用到输入序列的位置信息。
而位置信息在很多时候是比较重要的，比如在词性标记的场景中，动词就不容易出现在一个句子序列的开头。应该考虑在输入中加入位置信息的编码。

最早的transformer用的ei，就像涂上，每一个颜色，都代表一个向量，把向量分别在不同的位置相加得到，每一个位置都有一个专属的e。
这样的位置向量，是人为设定的，但是它会产生很多问题。比如我定义向量的时候它的长度只有128，但是sequence有129怎么办呢？
这个位置向量，是一个仍然待研究的问题。有各种各样不同的人为设定的位置向量，还可以让机器根据资料去自己学习出来。

10、self-attention在不同领域的应用

• 文本处理
  比如在文字处理的场景中，可以将单词表示为向量，将句子看作单词的序列，用Self-Attention对单词进行词性标记。

• 语音处理
  
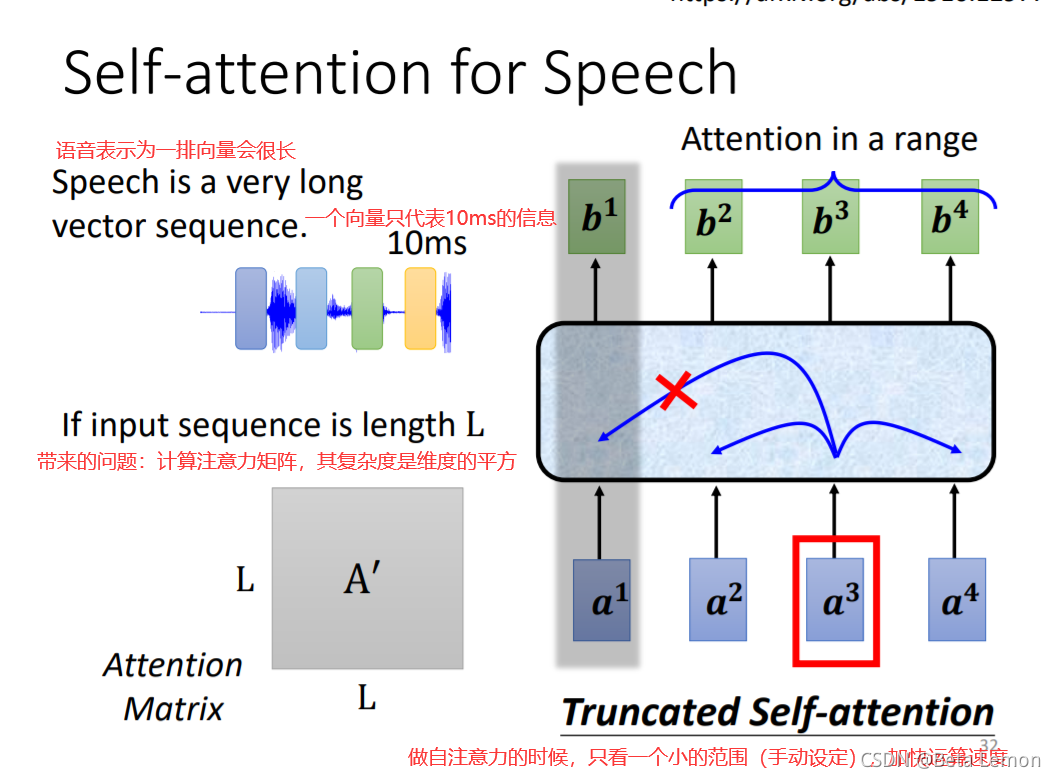
  比如在简化版的语音辨识的场景中，以将一小段音频表示为向量，将整段音频看作是小段音频的序列，用Self-Attention对小段音频的phonetic进行标记。
  需要注意的是，由于音频的序列会非常长，为了降低运算复杂度，同时考虑到某一小段音频仅与其前后一部分存在关联。并不需要将整段音频对应的向量序列都输入到Self-Attention中，仅将小段音频附近的向量序列输入Self-Attention中即可。

• 图像识别
  
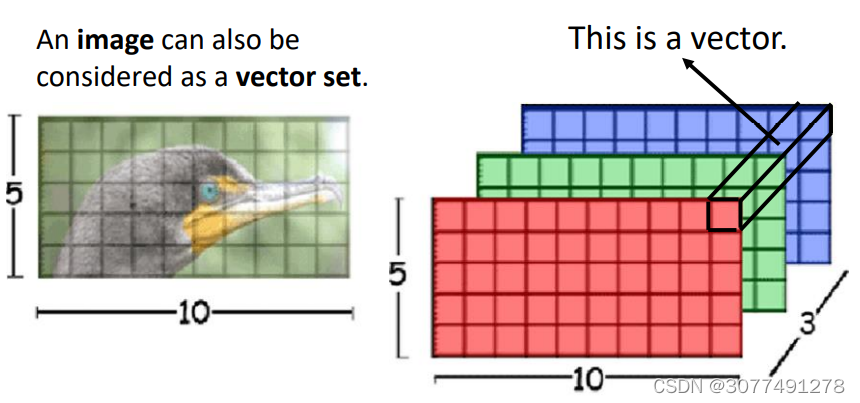
  在做CNN的时候，一张图片可看做一个很长的向量。它也可看做 一组向量：一张5 * 10的RGB图像可以看做5 ∗ 10的三个（通道）矩阵，把三个通道的相同位置看做一个三维向量。

• 对图(graph)的处理
  图中的每个节点也可以看做是一个向量，graph也可以看作是向量的集合。
  需要注意的是，可以利用图中节点本身的相连信息（边）考虑向量之间的相关性，比如没有边相连的节点可以认位这两个节点没有关联性，直接将其相关性设置为0。
  将Self-Attention的思想用于graph时，就是一种GNN的类型。

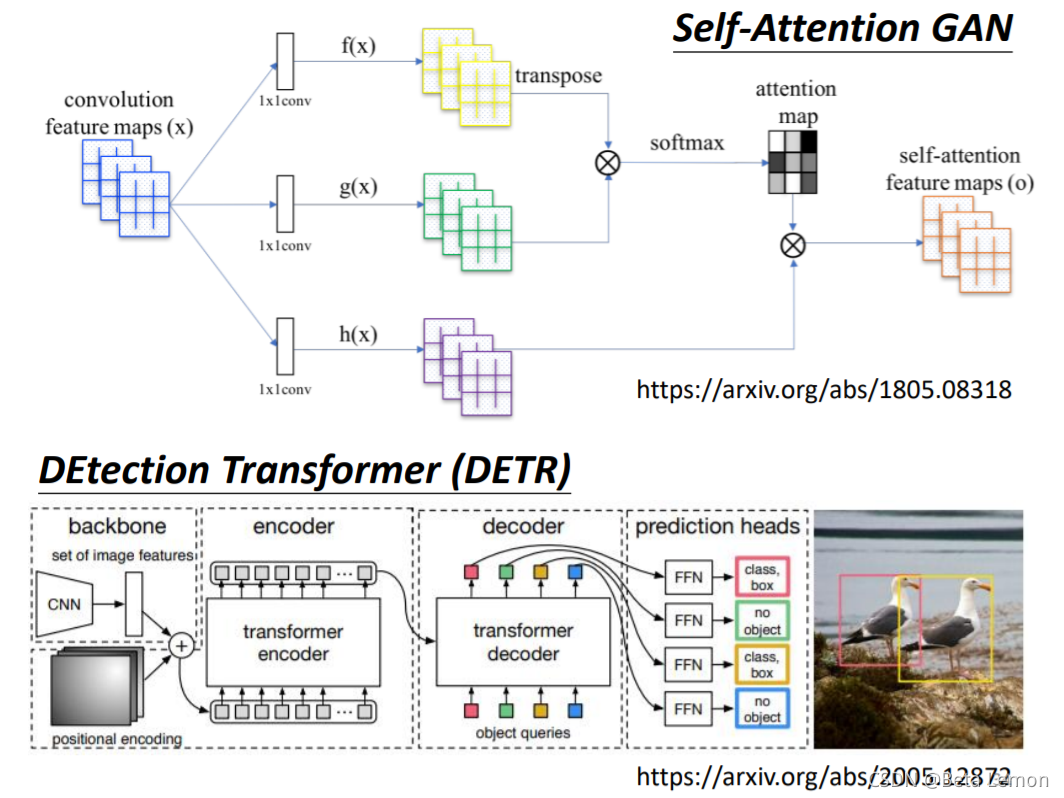
11、Self-attention v.s. CNN

• CNN看做简化版的self-attention：CNN只考虑一个感受野里的信息，self-attention考虑整张图片的信息

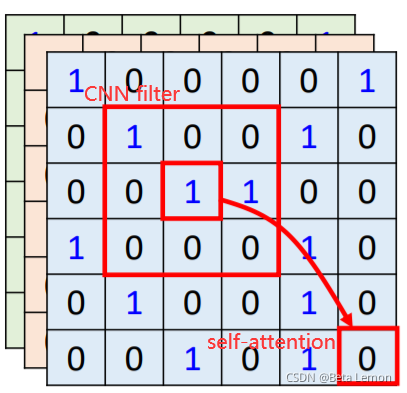
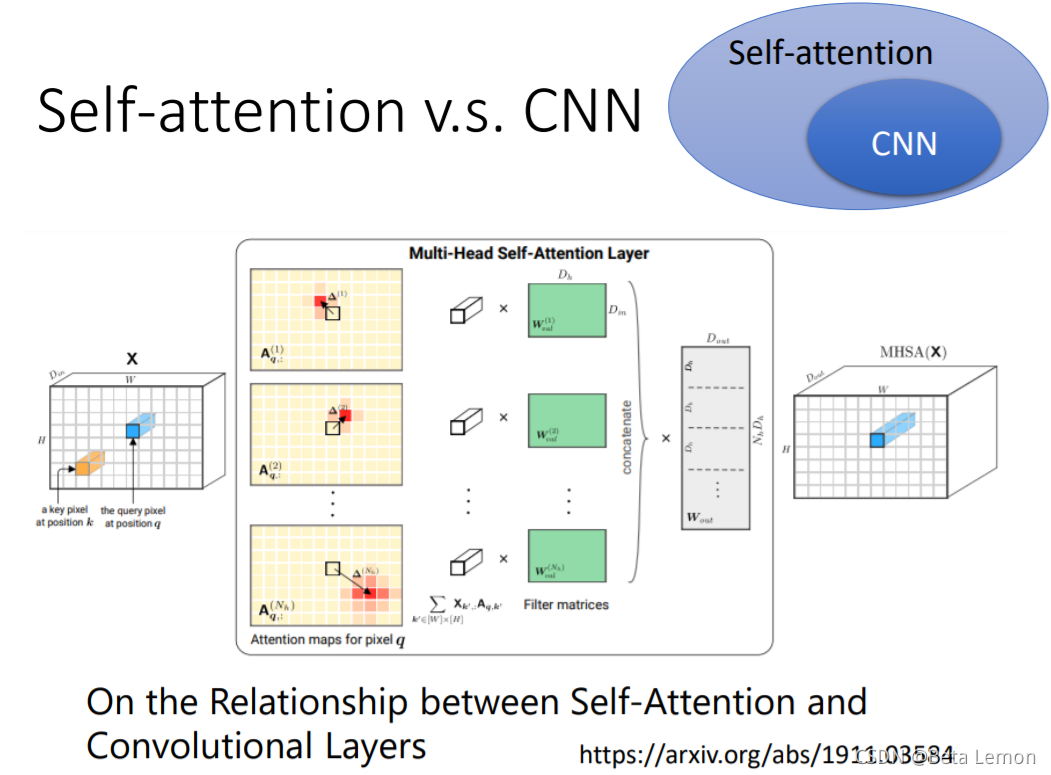
• self-attention是复杂版的CNN：CNN里面每个神经元只考虑一个感受野，其范围和大小是人工设定的；自注意力机制中，用attention去找出相关的像素，感受野就如同自动学出来的。

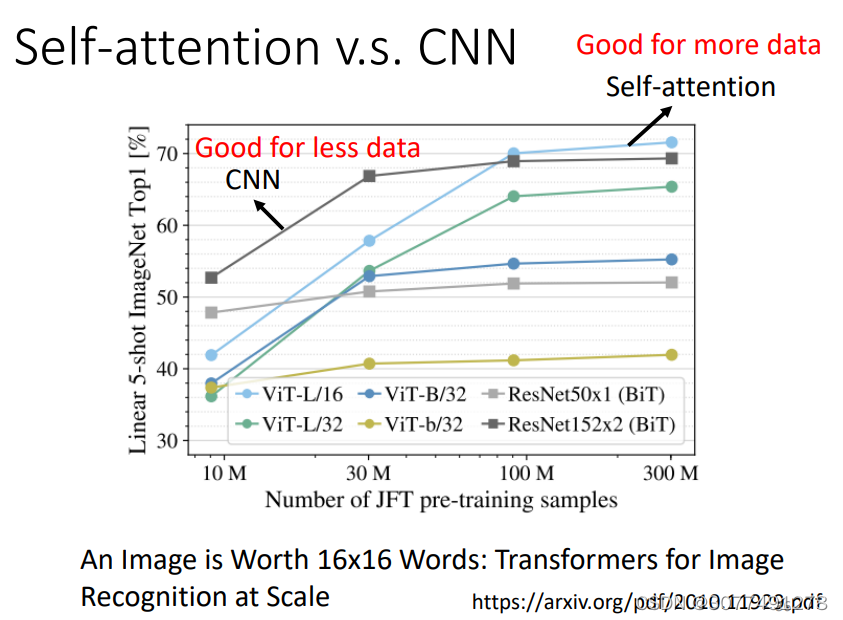
如果用不同的数据量来训练CNN和self-attention，会出现不同的结果。大的模型self-attention如果用于少量数据，容易出现过拟合；而小的模型CNN，在少量数据集上不容易出现过拟合。

12、Self-attention v.s. RNN

RNN主要有两个缺点，一是两边的向量在运算过程中对后续向量的影响可能会逐渐变小，二是输出向量无法并行计算产生。
因此很多的应用逐渐把RNN的架构改为Self-attention架构

12、Self-attention v.s. GNN

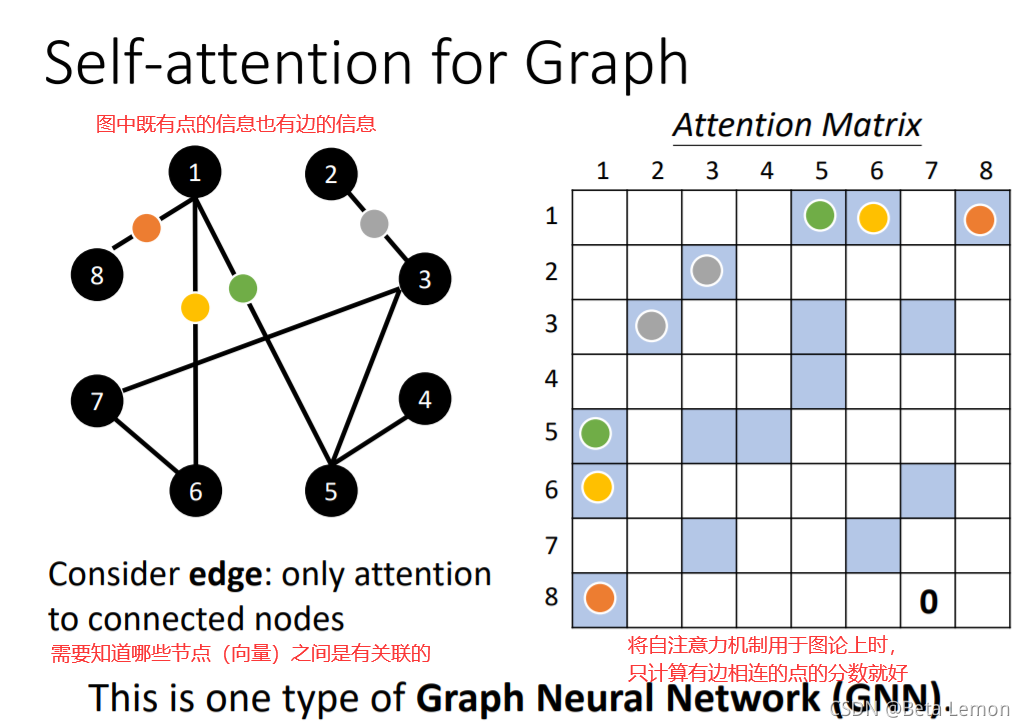
self-attention也可以用在GNN上面，在做attention matrix的时候，只需要计算有edge相连的node就好。

13、self-attention的变形

运算量会非常大（肯定的嘛，CNN就相当于是全连接去掉一些权重，把CNN进行简化），然后它会有各种各样的变形 ，最早的transformer，用的就是这个 ，广义的transformer就是指的self-attention。
我们可以看到，很多新的former，横轴表示比原来的transformer运算速度快 ，但是纵轴表示效果变差。

14、代码实现

self-attention

import torch
import torch.nn as nn
import math

class SelfAttention(nn.Module):
    """
    input : batch_size * seq_len * input_dim
	    q : batch_size * input_dim * dim_k
	    k : batch_size * input_dim * dim_k
	    v : batch_size * input_dim * dim_v
    """
    def __init__(self, input_dim, dim_k, dim_v):
        super().__init__()
        self.dim_k = dim_k
        self.q = nn.Linear(input_dim, dim_k)
        self.k = nn.Linear(input_dim, dim_k)
        self.v = nn.Linear(input_dim, dim_v)
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, x):
        Q = self.q(x)  # Q: batch_size * seq_len * dim_k
        K = self.k(x)  # K: batch_size * seq_len * dim_k
        V = self.v(x)  # V: batch_size * seq_len * dim_v

        attention = torch.bmm(self.softmax(torch.bmm(Q, K.permute(0, 2, 1)) / math.sqrt(self.dim_k)), V)

        return attention

Multi-Head Self-Attention

class MultiHeadSelfAttention(nn.Module):
    """
    input : batch_size * seq_len * input_dim
        q : batch_size * input_dim * dim_k
        k : batch_size * input_dim * dim_k
        v : batch_size * input_dim * dim_v
    """
    def __init__(self, input_dim, dim_k, dim_v, nums_head):
        super(MultiHeadSelfAttention, self).__init__()
        assert dim_k % nums_head == 0
        assert dim_v % nums_head == 0
        self.dim_k = dim_k
        self.dim_v = dim_v
        self.q = nn.Linear(input_dim, dim_k)
        self.k = nn.Linear(input_dim, dim_k)
        self.v = nn.Linear(input_dim, dim_v)

        self.nums_head = nums_head
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, x):
        Q = self.q(x).view(-1, x.shape[1], self.nums_head, self.dim_k // self.nums_head).permute(0, 2, 3, 1)
        K = self.k(x).view(-1, x.shape[1], self.nums_head, self.dim_k // self.nums_head).permute(0, 2, 3, 1)
        V = self.v(x).view(-1, x.shape[1], self.nums_head, self.dim_v // self.nums_head).permute(0, 2, 3, 1)

        attention = torch.matmul(self.softmax(torch.matmul(Q, K.permute(0, 1, 3, 2)) / math.sqrt(self.dim_k)),
                                 V).transpose(-2, -1)  # [batch_size, n_head, seq_len, hidden_size // n_head]
        attention = attention.transpose(1, 2)  # [batch_size, seq_len, n_head, hidden_size // n_head]
        
        output = attention.reshape(-1, x.shape[1], x.shape[2])	# [batch_size, seq_len, hidden_size]
        
        # 或
        # attention = attention.permute(2, 0, 1, 3)
        # output = torch.cat([_ for _ in attention], dim=-1)
		
        return output

参考文章：
李宏毅机器学习2021笔记—self-attention（上）
李宏毅机器学习2021笔记—self-attention（下）
李宏毅老师2022机器学习课程笔记 03 自注意力机制(Self-Attention)
李宏毅《深度学习》- Self-attention 自注意力机制
李宏毅老师Self-Attention，注意力机制的实现过程学习笔记