Manacher
Manacher
引子:
回文串:
当一个长度为n字符串中的任意第i个字符和第n-i+1个字符都相同时,我们称这个字符串回文。比如:a,aba,abba
子串:
当一个字符串A可以在字符串B中找到一段和它完全相同的字符串,我们称字符串A是字符串B的子串。比如:A:abba B: ccabbacccc
回文子串:
当一个字符串A既是B的子串,其本身又是一个回文串时,我们成A是B的回文子串。比如:B:asdsadaas \(A_1\) :a \(A_2\):s \(A_3\):aa \(A_4\):asdsa
问题来了——我们该如何求一个字符串的回文子串呢?
因为马拉车本身只是一个过于聪明的暴力,所以我们从暴力思路讲起。
暴力思路:
提取字符串的每一个子串,再判断该子串是否为回文串,记录最长回文子串的长度。时间复杂度为 O(\(n^3\)),这很劣了
暴力思路Pro:
众所周知,回文串有一个中心,这个中心或者是一个字符(当字符串长度为奇数如aba),或者是两个字符(字符串长度为偶数如abba)我们计算以每一个字符串为中心的回文子串的最长长度。从中心开始向两边遍历,若两边字符相同,长度+=2。
这样的话忽略掉了偶数长度的回文子串。那我们是否有必要取相邻两个相同的字符为中心再扫一遍呢?
考虑在两个字符中间添加一个字符,那么以这个字符为中心,就构成了一个长度为奇数的回文子串。因此,我们来预处理,在每两个字符之间添加一个这个字符串中绝对不会包含的字符(通常选择‘#’),为防止越界,在前端加上另一种不会出现的字符(通常选择‘$’)
时间复杂度为 O(\(n^2\)),还是很劣
暴力思路ProMax:
在暴力思路Pro的基础上,我们观察一下性质:因为回文串的性质,所以我们可以发现,在一个大回文串的左半部分如果存在一个小回文串,那么那个小回文串以大回文串回文中心为对称中心对称的位置,也是一个和该小回文串一模一样的回文串的回文中心。挂图为证:
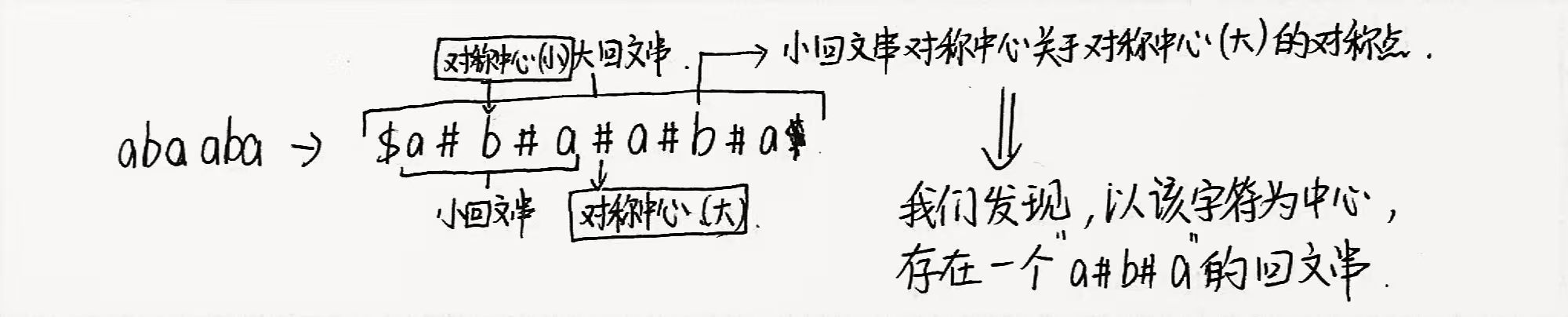
(就别管我的丑陋字迹了吧)
那么咱们就可以直接用左面小回文串的长度更新右面小回文串的长度
欸我是不是忘了说其实这就是Manacher思路了
Manacher:
- 在马拉车中,我们沿用了暴力Pro中的更新长度方式,向左右扫描,将扫描的结果记录在(int)d[]中。
- 为了实现左右对称回文子串的更新,我们应该记录大回文串的左右端点。所谓大回文串,其实指的是目前找到的右端点最靠右的回文串。为什么这么选择呢?因为我们是从左到右处理的,越靠右,向后遍历时可利用信息越多。在我们对称更新的过程中我们应该注意:因为有可能大回文串的左端点没有覆盖小回文串的左端点,那我们更新的时候要取右对称中心和大回文串右端点的距离 和 左回文串d[]值 的最小值,因为大回文串范围之右的字符一定不等于大回文串范围之左的字符,要不然当时d[]值会更新。
- 最后,我们如何更新大回文串呢?从大回文串的定义入手。上文说了“大回文串就是目前找到的回文串中右端点最靠右的那个”,所以当我们用暴力Pro方法更新右回文串长度时,判断一下右端点是否大于当前大回文串的右端点,如果大于就更新。
以上三段话就对应着manacher中的三个函数了。
那么代码如下:
if(i<=r)
{
d[i] = min(d[r - i + l], r - i + 1); //左右回文串对称法更新
}
while(ss[i-d[i]]==ss[i+d[i]]) //pro暴力法更新
{
d[i]++;
}
if(i+d[i]-1>r) //更新大回文串的左右端点
{
r = i + d[i] - 1;
l = i - d[i] + 1;
}
ans = max(ans, d[i] - 1);
然后再外面加上从左到右遍历的for循环就形成了manacher的运行部分
void Manacher()
{
ans = 0;
d[1] = 1;//d[]数组记录最长回文子串
for (int i = 2,l,r=0; i <= n;i++) //从左到右遍历
{
if(i<=r)
{
d[i] = min(d[r - i + l], r - i + 1);
}
while(ss[i-d[i]]==ss[i+d[i]])
{
d[i]++;
}
if(i+d[i]-1>r)
{
r = i + d[i] - 1;
l = i - d[i] + 1;
}
ans = max(ans, d[i] - 1);//实时更新答案
}
}
然后还有一个预处理:
inline void change()
{
int wow = s.size();
ss += "$#";//防止越界
for (int i = 1; i <= wow;i++)
{
ss += s[i-1];
ss += '#';//加入特殊字符
}
n = ss.size();//更新字符串长度
}
时间复杂度的证明:
打眼一看,O(n)的for循环中间加了一个while,这很像O(\(n^2\))了,那和普通暴力有什么区别呢?
我们发现,每一次的d[i]++都会使大回文串右端点向右移。
当一个右小串在大回文串中,且小串右端点+1之后还不会超出大串覆盖范围,那么当前串左和当前串右的字符一定不等(要不然对应的左串长度为什么没加?),那么while循环条件就不会满足,就不会影响时间复杂度。
因为大回文串右端点只会右移n次,除了while循环的代码也是O(n)的,那么可以看出,Manacher的时间复杂度真的是O(n)了。
那么我们来贴一个完整代码叭。
完整代码:
#include<bits/stdc++.h>
using namespace std;
string s,ss;
int n,ans;
int d[31451411];
inline void change()
{
int wow = s.size();
ss += "$#";
for (int i = 1; i <= wow;i++)
{
ss += s[i-1];
ss += '#';
}
n = ss.size();
}
void Manacher()
{
ans = 0;
d[1] = 1;
for (int i = 2,l,r=0; i <= n;i++)
{
if(i<=r)
{
d[i] = min(d[r - i + l], r - i + 1);
}
while(ss[i-d[i]]==ss[i+d[i]])
{
d[i]++;
}
if(i+d[i]-1>r)
{
r = i + d[i] - 1;
l = i - d[i] + 1;
}
ans = max(ans, d[i] - 1);
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> s;
change();
Manacher();
cout << ans << "\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号