标量方程求解

1 控制方程

控制方程如下：

\[\frac{\part u}{\part t} + \frac{\part f(u)}{\part x} = s(x), \quad x \in [a, b] \]

我们通过各种数值方法来完成上述方程的求解。本软件采用有限差分法来离散方程，为了编程的方便，暂时采用均匀网格。同时，暂时提供周期性边界条件。

2 网格

求解域为\([a,b]\)，采用周期性边界条件，采用均匀网格。一些标记和约定如下：

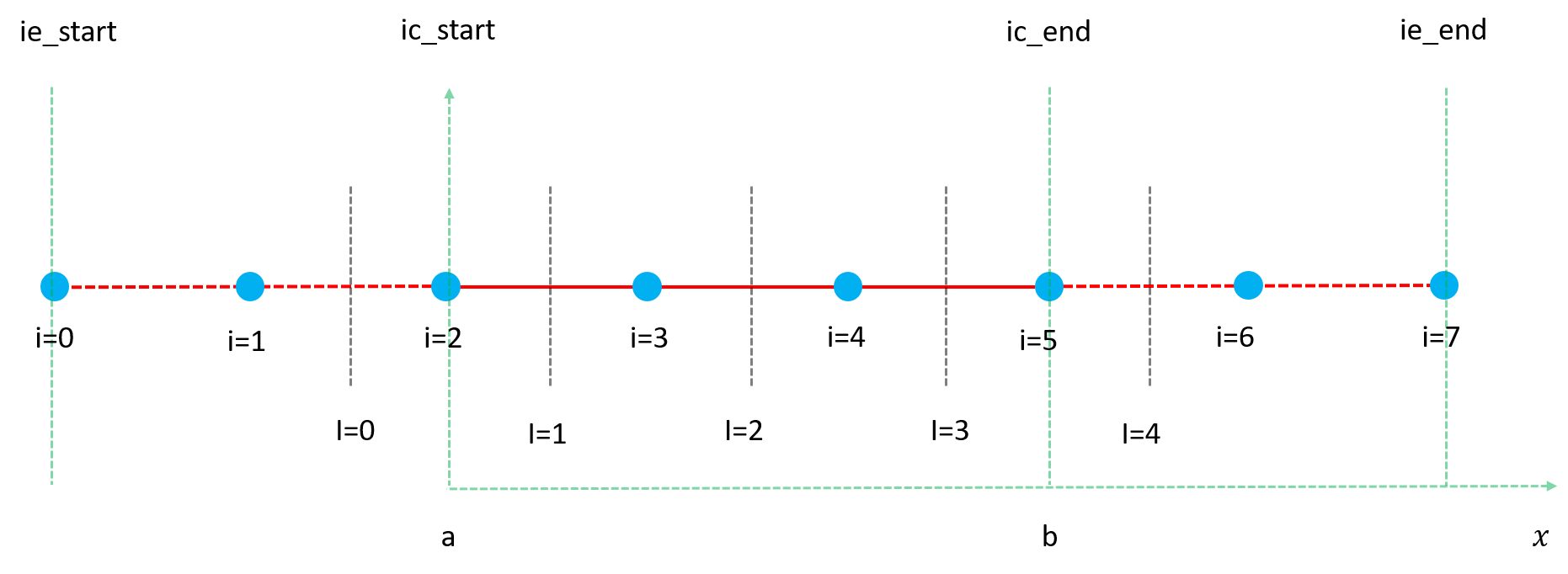
假设有网格n（n一般为奇数）个网格点，将[a,b]区间分为n-1份。虚拟单元有gmn层，则总体网格点数目为\(NT=n+2*gmn\)；图中的四条竖直虚线分别表示四个索引点，计算如下：

\[\begin{equation} \left\{ \begin{matrix} \begin{aligned} &ie\_start =0 \\ &ic\_start = gmn \\ &ic\_end = n + gmn - 1 \\ &ie\_end = n + 2 * gmn -1 \end{aligned} \end{matrix} \right. \end{equation} \]

创建数组x[NT]来储存网格点坐标，坐标计算如下：

\[\begin{equation} \left\{ \begin{matrix} \begin{aligned} &dx=\frac{b-a}{n-1} \\ &xe_{min} = a - gmn * dx \\ &xe_{max} = b + gmn * dx \\ &x_i=xe_{min} + i * dx, \quad x =0,1,\dots,NT \end{aligned} \end{matrix} \right. \end{equation} \]

3 场变量

创建数组\(u[NT]\)来储存场变量。创建数组\(Residual[n]\)来存储每个网格点对应的残差。我们将方程中\((s(x)-\frac{\part f(u)}{\part x})*dt\)整体的计算结果称为残差。

场变量初始化的时候，只给\([ic\_start, ic\_end]\)范围内的场变量赋值。虚拟网格上的物理量通过边界条件的处理来完成。

针对不同的物理问题，初始化方式不同。这里给出几个典型问题的初始化方法。

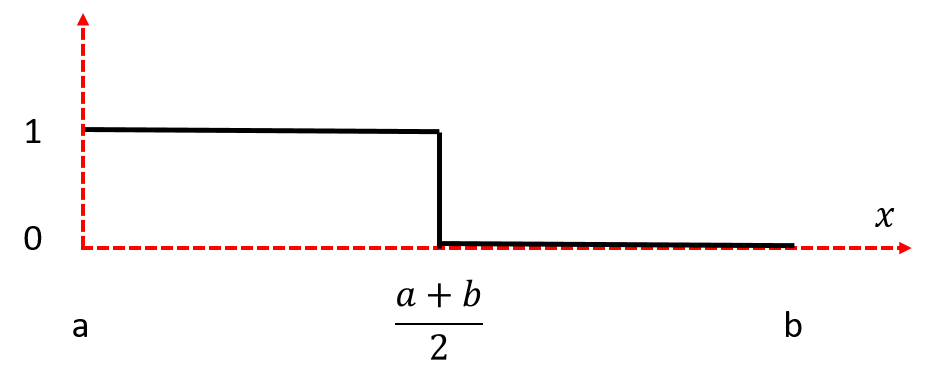
3.1 下阶梯函数

初始化如下：

\[\begin{equation} u(x,0)= \left\{ \begin{matrix} 1, \qquad x \le \frac{b-a}{2} \\ 0, \qquad x \gt \frac{b-a}{2} \end{matrix} \right. \end{equation} \]

初始化如下图：

初始化伪代码：

\[\begin{equation} \left\{ \begin{matrix} \begin{aligned} &u[i] = 1, \qquad i \in [ic\_start,\quad int\{\frac{ic\_end+ic\_start}{2}\}) \\ &u[i] = 0, \qquad i \in [int\{\frac{ic\_end+ic\_start}{2}\}, ic\_end] \end{aligned} \end{matrix} \right. \end{equation} \]

边界条件：

\[\begin{equation} \left\{ \begin{matrix} \begin{aligned} &u[i] = 1, \qquad i \in [ie\_start, \quad ic\_start) \\ &u[i] = 0, \qquad i \in [ic\_end+1, \quad ie\_end] \end{aligned} \end{matrix} \right. \end{equation} \]

3.2 正弦函数

初始化如下：

\[u(x,0)=sin(\frac{2\pi x}{b-a}) \]

初始化伪代码：

\[u[i] = sin(\frac{2\pi x[i]}{b-a}), \qquad i \in [ic\_start,\quad ic\_end] \]

边界条件（周期边界条件）：

\[\begin{equation} \left\{ \begin{matrix} \begin{aligned} &u[i] = u[ic_end-gmn + i], \qquad i \in [ie\_start, \quad ic\_start) \\ &u[i] = u[ic\_start-ic\_end + i], \qquad i \in [ic\_end+1, \quad ie\_end] \end{aligned} \end{matrix} \right. \end{equation} \]

3.3 组合波问题

典型的组合波问题如下：

1. 计算域：

\[a=-1,\quad b=1 \]

2. 初始值：

\[\begin{equation} u(x,0)= \left\{ \begin{matrix} \begin{aligned} &\frac{1}{6}(G(x,\beta,z-\delta)+G(x, \beta, z+\delta)+4G(x,\beta,z)), & -0.8 \le x \le -0.6; \\ &1, &-0.4 \le x \le-0.2; \\ &1-|10(x-0.1)|, & 0\le x \le 0.2 \\ &\frac{1}{6}(F(x, \alpha, a-\delta)+G(x, \alpha, a + \delta) + 4G(x,\alpha, a)), & 0.4 \le x \le 0.6 \\ &0, & otherwise \end{aligned} \end{matrix} \right. \end{equation} \]

其中：

\[\begin{equation} \left\{ \begin{matrix} \begin{aligned} &G(x,\beta,z)=e^{-\beta(x-z)^2} \\ &F(x,\alpha,z)=\sqrt{max(1-\alpha^2(x-a)^2,0)} \\ &a=0.5; \quad z=-0.7; \quad \alpha=10; \quad \beta=log2/(36\delta^2) \end{aligned} \end{matrix} \right. \end{equation} \]

3. 边界条件：周期性边界条件。

3.4 尖波与正弦波

1. 计算域：

\[a=-1,\quad b=1 \]

2. 初始值：

\[\begin{equation} u(x,0)= \left\{ \begin{matrix} \begin{aligned} &-xsin(\frac{3\pi}{2}x^2), & -1 \le x \le -1/3; \\ &|sin(2\pi x)|, &-\frac{1}{3} \lt x \le \frac{1}{3}; \\ &2x-1-\frac{1}{6}sin(3\pi x), & \frac{1}{3} \lt x \le 1 \\ \end{aligned} \end{matrix} \right. \end{equation} \]

3. 边界条件：周期性边界条件

4 空间重构

空间离散包含两个重要的步骤：场变量重构和通量分裂（中心格式不需要通量分裂技术）。本章主要介绍常见的（本程序实现的）一些场变量重构格式，在下一章将详细介绍本软件所实现的通量分裂技术。

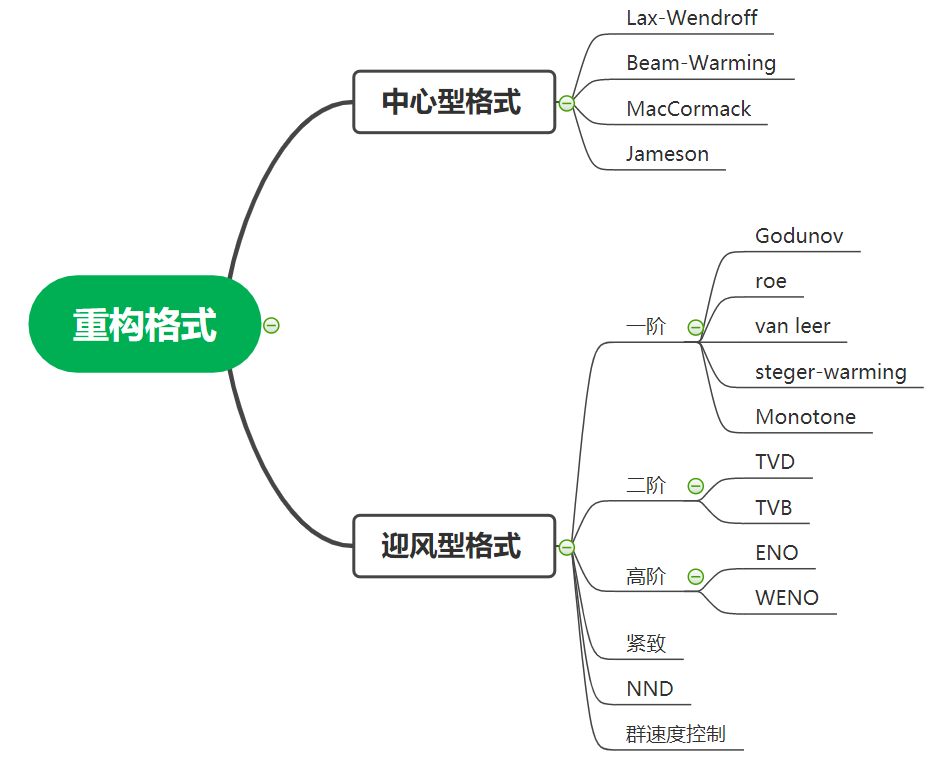
重构的主要目的是，通过单元值，计算单元界面之间的值（或者利用单元值插值得到半点值）。重构算法有中心型算法和迎风型算法两大类。主要分为如下：


4.1 一阶迎风格式

一阶迎风格式示意图如下：


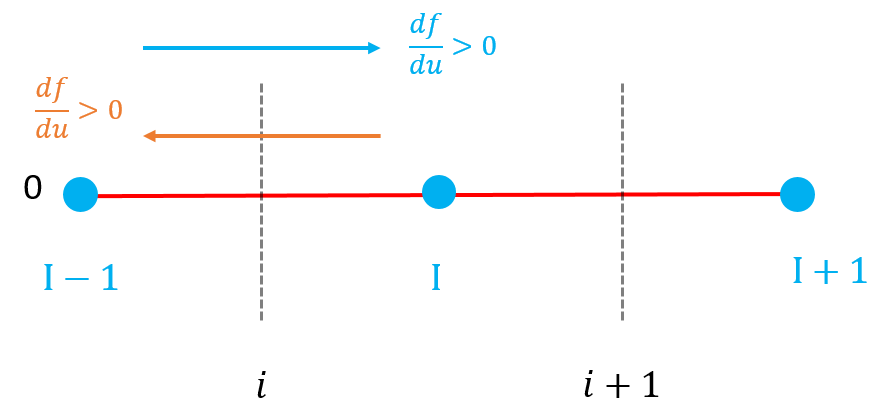
单元采用大写字母，界面采用小写字母。

对于第\(i\)个界面，其左侧值（后简称左值）\(up\)和右侧值（后简称右值）\(un\)，重构方式如下：

• 左值

  • 首先计算\(dfu=(\frac{df(u)}{du})|_{u=u_{I-1}}\)
  • 计算左值：
  \[up=\left\{ \begin{matrix} \begin{aligned} &u_{I-1} &if: dfu>0 \\ &u_I &if: dfu \le0 \end{aligned} \end{matrix} \right. \]

• 右值

  • 首先计算\(dfu=(\frac{df(u)}{du})|_{u=u_{I}}\)
  • 计算左值：
  \[un=\left\{ \begin{matrix} \begin{aligned} &u_{I-1} &if: dfu>0 \\ &u_I &if: dfu \le0 \end{aligned} \end{matrix} \right. \]

4.2 二阶中心格式

二阶中心格式重构如下：

\[up=un=\frac{u_I-u_{I-1}}{2\Delta x} \]

4.3 Jameson人工粘性

方程修正为：

\[\frac{\part u}{\part t} + \frac{\part f(u)}{\part x} = s(x)+\epsilon_2\frac{\part^2 u}{\part x^2}+\epsilon_4\frac{\part^4u}{\part x^4} \]

其中：

\[\epsilon_2=K_2|\frac{p_{i+1}+p_{i-1}-2p_i}{p_{i+1}+p_{i-1}+2p_i}| \]

\[\epsilon_4=max(0,(K_4-\epsilon_2)) \]

\[K_2=0.5\sim 1; \quad K_4=1/250 \sim 1/32 \]

二阶人工粘性在间断区提供大的粘性，用于捕捉激波；

四阶人工粘性提供基础粘性，保障计算稳定。

4.4 二阶迎风格式

\[u_{i+1/2}=u_{i-2}-4u_{i-1}+3u_i \]

4.5 NND格式

\[u_{i+1/2}=u_i+\frac{1}{2}minmod(\delta^+u_i,\delta^-u_i) \\ \delta^+u_i=(u_{i+1}-u_{i}) \\ \delta^-u_i=(u_i-u_{i-1}) \]

限制器：

\[\psi(r)=\left\{ \begin{matrix} \begin{aligned} &r &0<r\le1 \\ &1 &r>1\\ &0 &r<1 \end{aligned} \end{matrix} \right. \]

4.6 群速度控制格式

\[u_{i+1/2}=u_i+\psi(r)(u_{i+1}-u_i)/2 \]

限制器：

\[\psi(r)=\left\{ \begin{matrix} \begin{aligned} &r &|r|\le 1 \\ &1 &|r|>1 \end{aligned} \end{matrix} \right. \]

4.7 MUSCL格式

该格式由van Leer提出。

\[u_{i+1/2}=u_i+\frac{s}{4}[(1-\frac{s}{3})\delta^-u_i+(1+\frac{s}{3})\delta^+u_i] \\ s=\frac{2(\delta^-u_i)(\delta^+u_i)+\epsilon}{(\delta^+u_i)^2+(\delta^-u_i)^2+\epsilon} \\ \epsilon=10^{-6} \]

4.8 WENO格式

5. 通量分裂

6. 时间离散

时间离散分为两种：显式格式和隐式格式。

常见的显式格式有：

一阶显式欧拉差分方法、二阶TVD龙格库塔、三阶TVD龙格库塔、四阶非TVD龙格库塔。

设方程如下：

\[\frac{\part u}{\part t}=s(x)-\frac{\part f(u)}{\part x}=L(u) \]

6.1 一阶显式欧拉差分

推进如下：

\[\frac{u^{n+1}_i-u^n_i}{\Delta t}=L(u^n) \\ u^{n+1}_{i}=u_i^n+\Delta t L(u^n) \]

6.2 二阶TVD龙格库塔

推进如下：

\[u^{(1)}=u^n+ L(u^n) \Delta t\\ u^{n+1}=\frac{1}{2}(u^n+u^{(1)})+\frac{1}{2}L(u^{(1)})\Delta t \]

6.3 三阶TVD龙格库塔

推进如下：

\[u^{(1)}=u^n+\Delta L(u^n) \\ u^{(2)}=\frac{3}{4}u^n+\frac{1}{4}u^{(1)}+\frac{1}{4}L(u^{(1)})\Delta t \\ u^{n+1}=\frac{1}{3}u^n+\frac{2}{3}u^{(2)}+\frac{2}{3}L(u^{(2)})\Delta t \]

6.4 四阶TVD龙格库塔

推进如下：

\[u^{(1)}=u^n+\frac{1}{2} L(u^n) \Delta t\\ u^{(2)}=u^n+\frac{1}{2} L(u^{(1)}) \Delta t\\ u^{(3)}=u^n+ L(u^{(2)}) \Delta t\\ u^n=\frac{1}{3}(u^n+u^{(1)}+2u^{(2)}+u^{(3)})+\frac{1}{6} L(u^{(3)})\Delta t \]