浅谈递归--二叉树递归

从大一接触递归开始就觉得递归很难,然后就一直避开递归这个大头,最近重拾递归,对递归有一些更深入的理解了。此篇仅供参考，如有说错的地方，可以在评论区和我一起探讨（这个方法是我学牛客网的左程云老师的，很推荐大家去报名他的课，不是广告，大家根据自己的经济实力去决定）。

首先我们从最简单的递归开始--阶乘

public static int fn(int x){
	if (x == 1) {
	     return 1;
	}
	return x*fn(x-1);
}

递归的全过程就如下所示。

-->6*fn(5)

-->6*(5*fn(4)

-->6*(5*(4*fn(3)))

-->6*(5*(4*(3*fn(2))))

-->6*(5*(4*(3*(2*fn(1))))))

-->6*(5*(4*(3*(2*1))))

-->6*(5*(4*(3*2)))

-->6*(5*(4*6))

-->6*(5*24)

-->6*120

-->720

递归也就是系统自动帮我们压栈的过程，我们把前面还没办法计算出结果的计算压入栈，等遇到base case（return语句）时，就会弹出一个计算结果，最后一个个依次弹出，这就是整个递归的过程。这一段需要自己去画个栈结果，画出依次压入栈和弹栈的过程，才有更深刻的理解。

在这里因为比较简单，所以大家应该都能理解，但到了更加复杂的情况的时候，我们会发现，递归像玄学一样无法理解，为什么突然就能得出结果了。在这里我先介绍一下二叉树的递归套路。

（二叉树的递归遍历也能帮助我们去理解递归，我们可以去手动去试试看）

首先二叉树的递归套路，就是创建一个类为返回类型，而每一次递归都会返回一个“返回类型（ReturnType）",通过这个返回类型,我们就能很简单地得到结果。我把代码放出来大家就懂了。我先举例一个比较简单的，判断一颗二叉树是否为平衡二叉树，而判断是否为平衡二叉树，我们就需要去判断每一个节点的左右孩子的高度差，这就很符合我们的递归思想，所以我们去递归每个节点的时候，我们就返回两个关键信息，该节点的左孩子是否为平衡二叉树（boolean isB）和左孩子的最大高度（int hight），该节点的右孩子是否为平衡二叉树（boolean isB）和右孩子的最大高度（int hight）。

public class IsBanlenceTree {
	private static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}
	private static class ReturnType{
		private boolean isB;
		private int h;
		private ReturnType(Boolean isB,int h){
			this.isB = isB;
			this.h = h;
		}
	}
	private static boolean isB(Node head){
		return process(head).isB;
		
	}
	private static ReturnType process(Node head){
		//base case
		if(head == null){
			return new ReturnType(true, 0);
		}
		//黑盒
		ReturnType leftReturnType = process(head.left);
		if (!leftReturnType.isB) {
			return new ReturnType(false, 0);
		}
		ReturnType rightReturnType = process(head.right);
		if (!rightReturnType.isB) {
			return new ReturnType(false, 0);
		}
		//解黑盒过程
		if (Math.abs(leftReturnType.h - rightReturnType.h)>2 ) {
			return new ReturnType(false, 0);
		}
		int h = Math.max(leftReturnType.h, rightReturnType.h);
		return new ReturnType(true, h+1);
	}
}

这个递归方法有三个重要的部分，base case 和递归和递归返回值，我们可以把这的递归当成黑盒去理解，我们先不管为什么它就会返回值，而“递归返回值”的部分也就是我们解黑盒的过程。这就是二叉树递归套路的“理解套路”。但是我在一开始接触的时候，就很疑惑为什么这么递归，就能得到我们想要的值，这样看来递归确实是很像玄学。但是我们刚刚说了，递归其实就是系统帮我们自动压栈的过程，所以我们自己去理解的时候，可以画出一个栈结果出来。

假设我们的二叉树是长这个样子

 

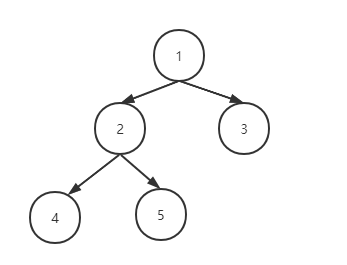
那我们递归压栈过程如下所示

 

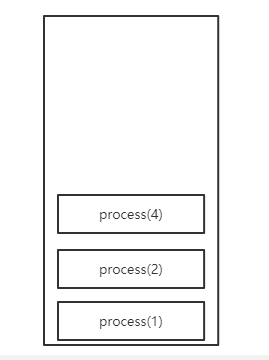
当压到这里的时候再继续要,我们压入的节点就为空,此时就出现了返回值。

 

 

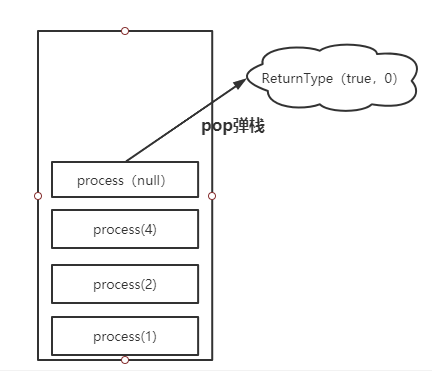
 当发生弹栈时，就会继续进行到ReturnType rightReturnType = process(head.right)，而此时的head.right也为空,这时也弹出一个返回类型return new ReturnType(true, 0);而这时你就能理解接黑盒的过程了。

if (Math.abs(leftReturnType.h - rightReturnType.h)>2 ) {
	return new ReturnType(false, 0);
}
   int h = Math.max(leftReturnType.h, rightReturnType.h);
   return new ReturnType(true, h+1);

　　这里的最后一个返回值为什么它就有值，就是因为我们的栈节点④弹出了它左右孩子的两个关键信息，此时左右孩子都为平衡二叉树，他们的最大高度为0，加上自己就为1。所以节点④也返回信息给到它的父节点②，父节点②如果得到了它的右孩子的信息，那么它就有能得到自己的返回类型。这就是递归的过程。

而类似的题还有，找到二叉树的最大距离和晚会最大活跃度。

二叉树的最大距离的解题思路就是，我需要左树的信息，也需要右树的信息，存在两个情况，

①X不参与：Math.max(左树得到的最大距离,右树得到的最大距离)

②X参与:左树的高+右树的高

所以我们的ReturnType需要有最大距离和最大高度,代码如下(以下是左程云老师的代码)

public class MaxDistanceInTree {
	public static class Node {
		public int value;
		public Node left;
		public Node right;
		public Node(int data) {
			this.value = data;
		}
	}
	public static class ReturnType{
		public int maxDistance;
		public int h;
		public ReturnType(int m,int h){
			this.maxDistance = m;
			this.h = h;
		}	
	}

	public static ReturnType maxDistance(Node head) {
		return process(head);
	}
	
	public static ReturnType process(Node head){
		if (head == null) {
			return new ReturnType(0, 0);
		}
		ReturnType leftReturnType = process(head.left);
		ReturnType rightReturnType = process(head.right);
		//三种情况
		int includeHeadDistance = leftReturnType.h +rightReturnType.h +1;
		int p1 = leftReturnType.maxDistance;
		int p2 = rightReturnType.maxDistance;
		//解黑盒
		int resultDistance = Math.max(Math.max(p1,p2),includeHeadDistance);//找到三种情况最大的
		int hitself = Math.max(leftReturnType.h,rightReturnType.h) + 1;//这里要计算自己的深度是为了递归的时候用到
		return new ReturnType(resultDistance, hitself);
	}

　　

 我每次理解的时候,都会去想压栈到最后一个弹出栈时弹出的是什么,由此去想我们解黑盒是要怎么做,这是我去理解二叉树递归套路的思路,每个人都有自己的理解,你也可以找到适合自己的方式。（最后，推荐一下左程云老师的课，因为贴了老师的代码，而且左程云老师确实讲的特别好，有条件的小伙伴可以去了解一下https://www.nowcoder.com/courses/cover/live/429）