回溯实战篇1
前言
上文带大家学习了回溯的理论基础,如果没看过的点这去回顾下 回溯理论篇 - carpell - 博客园,今天带大家进行回溯的实战篇1,去学习如何用回溯的方法去解决组合的问题,最重要的就是学会回溯三部曲的构建,一文带大家弄懂。本文用于记录自己的学习过程,同时向大家进行分享相关的内容。本文内容参考于代码随想录同时包含了自己的许多学习思考过程,如果有错误的地方欢迎批评指正!

组合
组合

相关技巧:首先看题,最简单的就是依照暴力法来写for循环解题,但是有个需要注意的地方就是,我们需要根据k的值来写多少层for循环,k为多少,for循环就多少层。两层三层的好写,但是二十层三十层的怎么办,也都写出来吗,这当然就是不现实的了。所以这道题怎么解,用回溯。
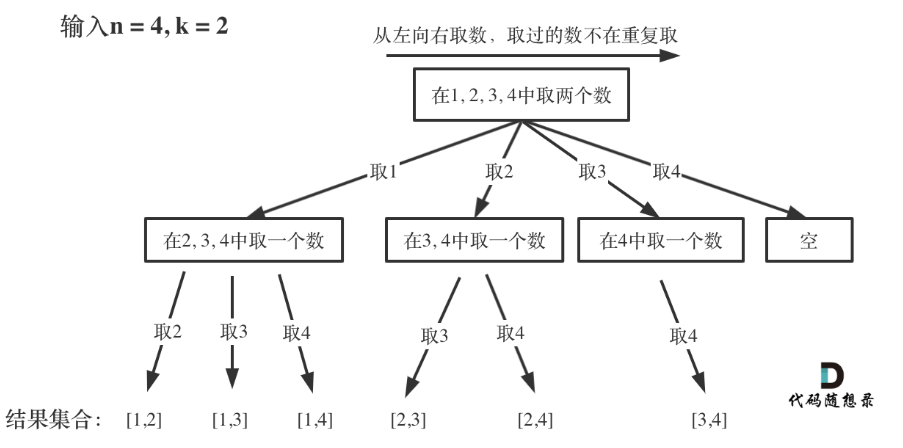
首先我们要知道,所有的回溯问题,我们都是可以抽象为树形结构来理解的。如图就是非常的一目了然了,我们来通过一个成功的结果来思考我们该如何去通过回溯方法来写代码。首先我们有1,2,3,4,那么我们从中取两个作为结果集,首先取了[1],然后我们是不是该从1后面的数字中再来取了,所以选择范围就变成了2,3,4,然后再取2,就变成了[1,2],那么其是不是符合题目的要求了呢,所以加入结果,退出单层回溯,退出之后,就该弹出取的2了,记住回溯的要点,有得就会有失,是对应的。所以这样再来看我们的回溯三部曲就能够很好的写出来了。
- 确定回溯的参数和返回值:我们来看回溯参数,n和k肯定是需要的,然后我们还需要个srartindex用来记录当前从哪里开始,并且在每下个回溯的时候,需要在当前的基础上加1,这样我们就避免了重复的可能。还有我们需要有一个参数path来存储我们的路径,用来加入新的和弹出操作,最后当结果符合,我们肯定需要一个result来保存我们的结果。这就是我们组合问题中所需要的参数了。至于返回值就不需要了,因为我们有result参数来保存我们的结果了。
- 确定回溯的终止条件:就是当我们的路径长度符合我们的要求的时候,就是回溯的终止了。
- 确定单层回溯的逻辑:首先判断我们的路径长度是否符合要求,符合要求就回溯终止,不符合就继续回溯过程,然后从srartindex开始加入新的,再进入回溯,回溯退出之后一定要弹出当前回溯中进入的数。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result=[]
self.backtracking(n,k,1,[],result)
return result
def backtracking(self,n,k,srartindex,path,result):
if len(path) == k:
result.append(path[:])
return
for i in range(srartindex,n+1):
path.append(i)
self.backtracking(n,k,i+1,path,result)
path.pop()
电话号码的字母组合

相关技巧:这道题其实跟组合问题是异曲同工的,只不过这里每个数字代表了不同的字符,每次从不同数字代表的字符集中来取就行了。
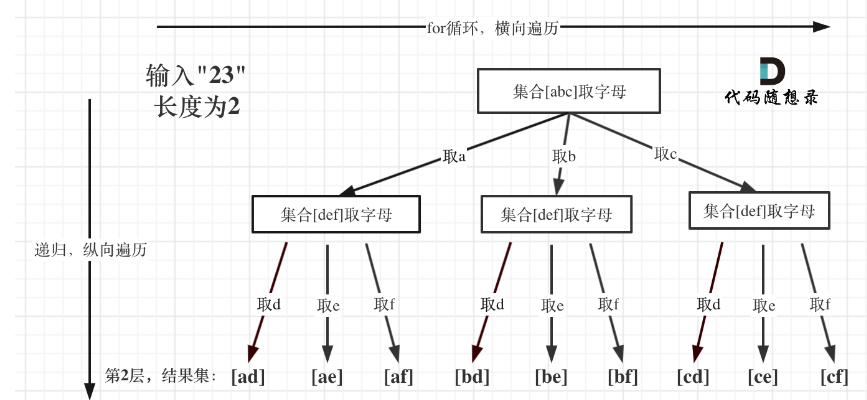
我们来通过一个成功的结果来思考我们该如何去通过回溯方法来写代码。首先我们有23数字,其代表着两个不同的字符集,所以这里我们需要有个map映射,不同的数字指向不同的字符集。那么我们的任务就是从每个字符集中取一个作为结果集,首先从2代表的字符集[abc]取了[a],然后我们是不是该从3代表的字符集取了,所以选择范围就变成了[def],怎么从2代表的字符集到3代表的字符集呢?我们可以用个index参数来确定,即通过digits[index]取出不同的数字所代表的字符集,然后再从[def]取,取出d就变成了[ad],那么其是不是符合题目的要求了呢,所以加入结果,退出单层回溯,退出之后,就该弹出取的d了,记住回溯的要点,有得就会有失,是对应的。所以这样再来看我们的回溯三部曲就能够很好的写出来了。
- 确定回溯的参数和返回值:我们来看回溯参数,digits肯定是需要的,然后我们还需要个index用来记录当前到哪个数字了,并且在每下个回溯的时候,需要在当前的基础上加1,这样我们就避免了重复的可能。还有我们需要有一个参数s来存储我们的路径,用来加入新的和弹出操作,最后当结果符合,我们肯定需要一个result来保存我们的结果。这就是我们组合问题中所需要的参数了。至于返回值就不需要了,因为我们有result参数来保存我们的结果了。
- 确定回溯的终止条件:就是当我们的路径长度等于digits的长度的时候,就符合我们的要求了,就是回溯的终止了。
- 确定单层回溯的逻辑:首先判断我们的路径长度是否符合要求,符合要求就回溯终止,不符合就继续回溯过程,然后从通过index参数确定到哪个数字了,在取出其所对应的字符集。我们就可以写循环了,加入新的,再进入回溯,回溯退出之后一定要弹出即删除当前回溯中进入的字符。
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
self.result = []
self.s = ""
def backtracking(self, digits, index):
if index == len(digits):
self.result.append(self.s)
return
digit = int(digits[index]) # 将索引处的数字转换为整数
letters = self.letterMap[digit] # 获取对应的字符集
for i in range(len(letters)):
self.s += letters[i] # 处理字符
self.backtracking(digits, index + 1) # 递归调用,注意索引加1,处理下一个数字
self.s = self.s[:-1] # 回溯,删除最后添加的字符
def letterCombinations(self, digits):
if len(digits) == 0:
return self.result
self.backtracking(digits, 0)
return self.result
组合总和

相关技巧:这道题其实跟组合问题是一样的,唯一的不同就是,我们这里可以取重复的元素了,我们之前组合问题是通过进入下个回溯前将startindex+1传入下个回溯来避免重复的,那么现在我们可以重复了就不需要再进行+1操作了。
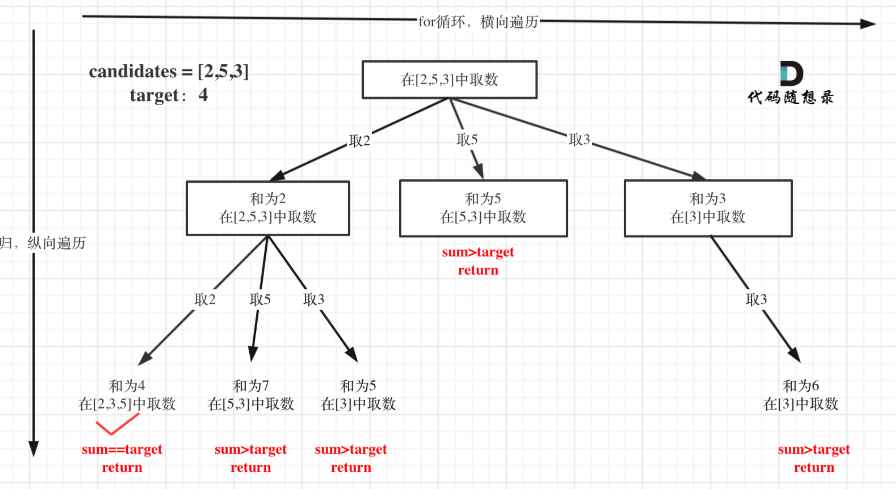
我们来通过一个成功的结果来思考我们该如何去通过回溯方法来写代码。首先我们有[2,5,3],那么我们从中取n个数,当其和符合我们的要求的时候作为结果集。首先取了[2],total(即总和)为2,还没符合条件,然后我们应该继续取,但是题目中给要求是可以重复的,所以选择范围还是[2,5,3],然后再取2,total就变成了4,那么这个时候会出现两种情况,要么等于target符合条件,加入结果,退出单层回溯,要么大于target不符合要求直接退出回溯。退出之后,就该弹出取的2了,这里的弹出就是不仅需要路径弹出2,同时也需要total减去2,记住回溯的要点,有得就会有失,是对应的。所以这样再来看我们的回溯三部曲就能够很好的写出来了。
- 确定回溯的参数和返回值:我们来看回溯参数,candidates和target肯定是需要的,然后我们还需要个startindex用来记录当前到哪个数字了,并且在每下个回溯的时候,这里就不要再加1了,这样我们就可以重复取。还有我们需要有path来存储路径,用来加入新的和弹出操作,和参数total来存储我们的结果和,最后当结果符合,我们肯定需要一个result来保存我们的结果。这就是我们组合问题中所需要的参数了。至于返回值就不需要了,因为我们有result参数来保存我们的结果了。
- 确定回溯的终止条件:这个时候回溯的终止条件就跟之前不一样了,之前的数都是确定的,但是现在不确定了,我们是通过其和total来判断是不是符合条件,其实看叶子节点也能知道,回溯的终止条件就两个,要么total符合条件,要么total>target,都是退出回溯,不过符合的加入结果集,不符合的直接返回就行了。
- 确定单层回溯的逻辑:首先判断我们的total是否到了终止条件,不符合就继续回溯过程,然后从通过startindex参数确定到我们可以取的集合,在取出数字进行加。我们就可以写循环了,路径加入新的,total加上新的值,再进入回溯,回溯退出之后,路径一定要弹出即删除当前回溯中进入的数字,并且total也要减回去。
class Solution:
def backtracking(self, candidates, target, total, startIndex, path, result):
if total > target:
return
if total == target:
result.append(path[:])
return
for i in range(startIndex, len(candidates)):
total += candidates[i]
path.append(candidates[i])
self.backtracking(candidates, target, total, i, path, result) # 不用i+1了,表示可以重复读取当前的数
total -= candidates[i]
path.pop()
def combinationSum(self, candidates, target):
result = []
self.backtracking(candidates, target, 0, 0, [], result)
return result
组合总和II

相关技巧:这道题其实跟组合总和是相似,但是这里出现了个不同的情况,其中candidates出现了重复的数,我们可以取重复的数。当然每个数还是只能取一次。所以我们如果还是按照求组合总和的逻辑去做会出现个什么问题呢?就是比如说有个[1,1,1,2],我们需要target为4,我们取了前两个1和最后的2组成了[1,1,2]=4符合要求,在后面的时候,又取了第2,3个1和2组成了[1,1,2]=4符合要求,看着我们好像取了不同的,但是最后的结果是一样的,我们该如何去避免这样的情况,也就是去重的,就是通过一个used数组。
怎么具体使用used,就是used[0,0,0,0]代表都没使用过,当candidates[i-1] == candidates[i]的时候,只有当candidates[i-1]的used是使用过的,我们才能使用candidates[i],这样我们就能够避免刚才所说的那个重复的情况了。就是换句话说,同一个树枝上面能出现相同的,但是同一层上面不行,从而避免了重复,可能是有点抽象哈,看看下图好好理解下,想一下整个过程就能清楚了。
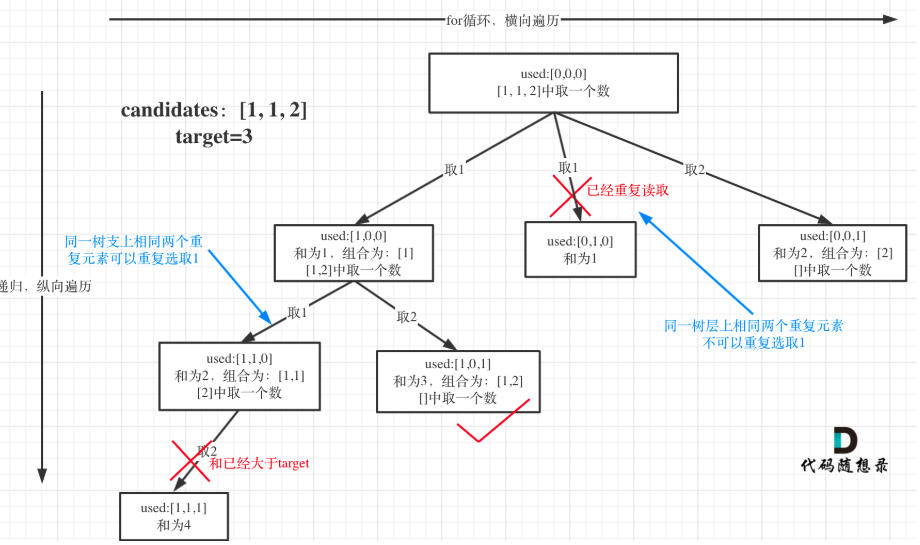
我们来通过一个成功的结果来思考我们该如何去通过回溯方法来写代码。首先我们有candidates[1,1,2],那么我们从中取数,当其和符合我们的要求的时候作为结果集。首先取了第一个的1,used就变为[1,0,0],total(即总和)为1,还没符合条件,然后我们应该继续取,然后再取第2个1,这个时候candidates[i-1] == candidates[i],并且used[1,0,0],所以我们可以取1,total就变成了2,那么这个时候还没符合条件,继续取2,total为4,这个时候要么等于target符合条件,加入结果,退出单层回溯,要么大于target不符合要求直接退出回溯。所以不符合,退出回溯之后,就该弹出取的2了,这里的弹出就是不仅需要路径弹出2,同时也需要total减去2,记住回溯的要点,有得就会有失,是对应的。然后就到回溯到了取第一个1的时候,即total=1,used[1,0,0],然后再取2,符合条件加入结果集。所以这样再来看我们的回溯三部曲就能够很好的写出来了。
- 确定回溯的参数和返回值:我们来看回溯参数,candidates和target肯定是需要的,还要个used数组记录数字是否被使用过。然后我们还需要个startindex用来记录当前到哪个数字了,并且在每下个回溯的时候,这里要再加1,这样我们就避免重复选取。还有我们需要有path来存储路径,用来加入新的和弹出操作,和参数total来存储我们的结果和,最后当结果符合,我们肯定需要一个result来保存我们的结果。这就是我们组合问题中所需要的参数了。至于返回值就不需要了,因为我们有result参数来保存我们的结果了。
- 确定回溯的终止条件:这个时候回溯的终止条件就跟组合总和的一样,都是通过其和total来判断是不是符合条件,其实看叶子节点也能知道,回溯的终止条件就两个,要么total符合条件,要么total>target,都是退出回溯,不过符合的加入结果集,不符合的直接返回就行了。
- 确定单层回溯的逻辑:首先判断我们的total是否到了终止条件,不符合就继续回溯过程,然后从通过startindex参数确定到我们可以取的集合,在取出数字进行加之前我们需要有个判断candidates[i] == candidates[i - 1] and not used[i - 1]才进入循环。我们就可以写循环了,路径加入新的,total加上新的值,再进入回溯,回溯退出之后,路径一定要弹出即删除当前回溯中进入的数字,并且total也要减回去,还有used也要记得改哦。
class Solution:
def backtracking(self, candidates, target, total, startIndex, used, path, result):
if total == target:
result.append(path[:])
return
for i in range(startIndex, len(candidates)):
# 对于相同的数字,只选择第一个未被使用的数字,跳过其他相同数字
if i > startIndex and candidates[i] == candidates[i - 1] and not used[i - 1]:
continue
if total + candidates[i] > target:
break
total += candidates[i]
path.append(candidates[i])
used[i] = True
self.backtracking(candidates, target, total, i + 1, used, path, result)
used[i] = False
total -= candidates[i]
path.pop()
def combinationSum2(self, candidates, target):
used = [False] * len(candidates)
result = []
candidates.sort()
self.backtracking(candidates, target, 0, 0, used, [], result)
return result
组合总和III

相关技巧:这道题其实跟组合问题可以说是一模一样的了,只不过这里多了些要求,要求k个数相加为n,做过了组合总和跟组合总和II,再来做这个就好理解的多了,不重复,长度有要求。
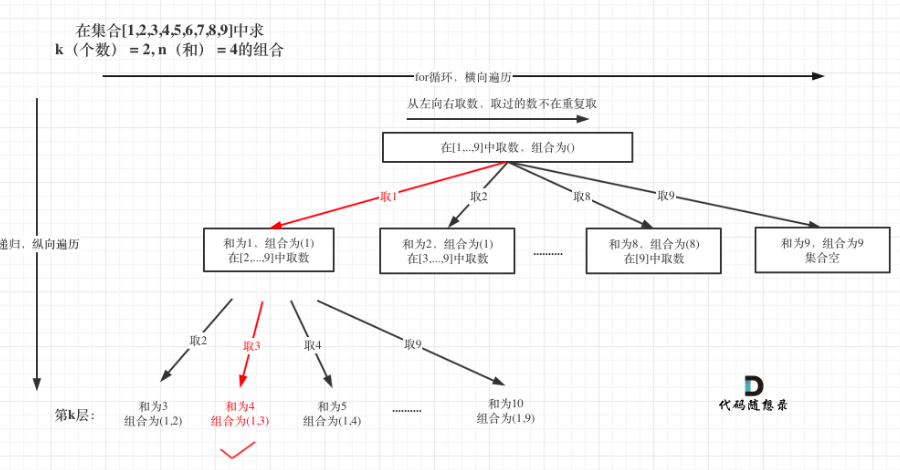
我们还是来通过一个成功的结果来思考我们该如何去通过回溯方法来写代码。首先我们的范围是[1...9],首先取[1],然后我们是不是该从1后面的数字中再来取了,所以选择范围就变成了[2...9],然后再取2,就变成了[1,2],currentSum就变成了3,那么其不是符合题目的要求的,所以回溯,退出2,currentSum并减去。然后加入[3],currentSum就变成了4,符合要求所以加入结果,退出单层回溯,退出之后,就该弹出取的2了,记住回溯的要点,有得就会有失,是对应的。所以这样再来看我们的回溯三部曲就能够很好的写出来了。
- 确定回溯的参数和返回值:我们来看回溯参数,targetSum和k肯定是需要的,然后我们还需要个srartindex用来记录当前从哪里开始,并且在每下个回溯的时候,需要在当前的基础上加1,这样我们就避免了重复的可能。还需要有个数currentsum来记录我们当前的和是多少了。还有我们需要有一个参数path来存储我们的路径,用来加入新的和弹出操作,最后当结果符合,我们肯定需要一个result来保存我们的结果。这就是我们组合问题中所需要的参数了。至于返回值就不需要了,因为我们有result参数来保存我们的结果了。
- 确定回溯的终止条件:就是当我们的路径长度符合我们的要求并且我们的currentSum符合targetSum的时候,就是回溯的终止了。
- 确定单层回溯的逻辑:首先判断我们的currentSum是否大于targetSum,如果大于就没必要再去看了,因为肯定不符合了。然后再看路径长度是否符合要求,符合要求且就回溯终止,且当currentSum等于targetSum就加入结果集。不符合就继续回溯过程,然后从srartindex开始加入新的,再进入回溯,回溯退出之后一定要弹出当前回溯中进入的数,currentSum也一定要减去。
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
result = [] # 存放结果集
self.backtracking(n, k, 0, 1, [], result)
return result
def backtracking(self, targetSum, k, currentSum, startIndex, path, result):
if currentSum > targetSum: # 剪枝操作
return # 如果path的长度等于k但currentSum不等于targetSum,则直接返回
if len(path) == k:
if currentSum == targetSum:
result.append(path[:])
return
for i in range(startIndex, 9 - (k - len(path)) + 2): # 剪枝
currentSum += i # 处理
path.append(i) # 处理
self.backtracking(targetSum, k, currentSum, i + 1, path, result) # 注意i+1调整startIndex
currentSum -= i # 回溯
path.pop() # 回溯



 浙公网安备 33010602011771号
浙公网安备 33010602011771号