拉格朗日乘子法 学习笔记

本来是想写支持向量机的学习笔记的然后觉得内容太多了越写越不想写于是咕掉了。
把写好的拉格朗日乘子法发上来吧QwQ

拉格朗日乘子法

wiki链接

拉格朗日乘子法用来求解带多个等式约束的情况下的多元函数极值。

它将一个有n个变量与m个约束条件的最优化问题转换为一个解有n + m个变量的方程组的解的问题。

单约束

考虑平面上的情况：

$$\max f(x,y)\\ s.t.\ g(x,y)=0$$

引入Lagrange multiplier $\lambda$ ，构造Lagrange function:

$$F(x,y,\lambda) = f(x,y) - \lambda \cdot g(x,y)$$

则f的极值点是F的驻点，F的驻点也不一定是f的极值点。

intuition：f的最大值，意味着f值不会沿着某个g=0的方向上升。在$g\equiv 0$的方向上，$\lambda$不再影响，f最大值就是F最大值。从下面的contour图可以直观看出。

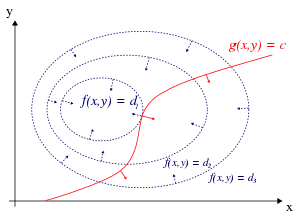
所以，要找g=0与f的contour方向相同的点，这个时候可能是f的最大值。（切点或者重合的一段contour）

注意到gradient是垂直于contour的，所以此时f与g的梯度方向相同或相反，大小不定，即满足：$\nabla_{x,y} f = \lambda \nabla_{x,y} g$

可以发现：

$$\nabla _{x,y,\lambda} F(x,y,\lambda) = 0$$

等价于

$$\begin{equation} \left\{ \begin{array}{l} \nabla_{x,y} f(x,y) = \lambda \nabla_{x,y} g(x,y) \\ g(x,y) = 0 \end{array} \right. \end{equation}$$

所以f的最大值点就是F的驻点啦！

多约束

$\mathbf{x}$为n维向量，有m个约束

lagrange function：

$$F(\mathbf{x},\mathbf{\lambda}) = f(\mathbf{x}) - \sum_{i=1}^m\lambda_ig_i(\mathbf{x})$$

此时取最大值时$f$的梯度为$g_1, g_2, ... , g_m$的梯度的线性组合。

每个限制是一个超平面，$g_i=0$的可行方向空间就是垂直于$\nabla g_i$ 的向量空间。考虑所有的限制后， 可行方向空间$A$就是所有$\nabla g_i$生成的空间$S$的正交补。

则$\nabla f(x) \in A^{\bot} = S$，所以就是线性组合啦！

同样的:

$$\nabla F = 0$$

等价于

$$\begin{equation} \left\{ \begin{array}{l} \nabla_{\mathbf{x}} f(\mathbf{x}) = \sum_{i=1}^m \lambda_i \nabla_{} g_i(\mathbf{x}) \\ g_i(\mathbf{x}) = 0, \ \forall i=1..m \end{array} \right. \end{equation}$$

而$\nabla F = 0$得到的就是一个n+m个方程的方程组。