误差反向传播法一 一个高效计算权重以及偏置量的梯度方法
ReLU 反向传播实现
class Relu: def _init_(self): self.x = None def forward(self,x): self.x = np.maximum(0,x) out = self.x return out def backward(self,dout):#检查self.x中的元素是否小于或等于0。对于所有小于或等于0的元素,对应的dx中的元素被设置为0。这通常用于实现ReLU(Rectified Linear Unit)激活函数的反向传播,因为ReLU函数在正数时保持原值,在负数时输出为0,其导数在正数时为1,在负数时为0。 dx = dout dx[self.x <=0]= 0 return dx
Sigmoid 反向传播实现
class_sigmoid: def init_(self): self.out=None def forward(self,x): out = 1/(1+np.exp(-x)) self.out = out return out def backward(self,dout): dx = dout *self.out*(1-self.out) return dx
Affine 层的实现
y=f(Wx+b)
其中,x是层输入,w是参数,b是一个偏置量。f是一个非线性激活函数。&nbsp;Affine层通常被加在卷积神经网络(CNN)或循环神经网络(RNN)等复杂网络结构的顶层,以输出最终的预测结果。
class Affine: def __init__(self,w,b): self.W= W self.b=b self.x = None self.dw = None self.db = None def forward(self,x): self.x = x out = np.dot(x,self.W) + self.b return out def backward(self,dout): dx= np.dot (dout,self.w.T) self.db = np.sum(dout,axis=0) #这一行计算偏置的梯度。dout是输出层的梯度,np.sum(dout, axis=0)沿着第一个轴(axis=0)对dout进行求和,这通常意味着对样本进行求和,得到偏置的梯度。 self.dw = np.dot(self.x.T,dout) #这一行计算权重的梯度。self.x是输入数据,self.x.T是输入数据的转置,np.dot(self.x.T, dout)计算输入数据的转置与输出层梯度的点积,得到权重的梯度。 return dx
Softmaxwithloss层的实现
由Softmax层和交叉熵损失层(Cross Entropy Error Layer)组合而成,主要用于多分类问题的训练和评估。
假设网络最后一层的输出为z,经过Softmax后输出为p,真实标签为y(one-hot编码)
其中,C表示共有C个类别,那么损失函数为
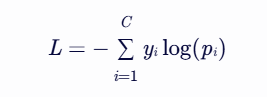
class SoftmaxwithLoss: def___init__(self): self.loss = None #损失 self.p = None # Softmax 的输出 self.y = None #监督数据代表真值,one-hot vector def forward(self,x,y): self.y =y self.p = softmax(x) self.loss = cross_entropy_error(self.p,self.y) return self.loss def backward(self,dout=1): batch_size = self.y.shape[0] dx = (self.p- self.y) / batch_size 归一化处理 return dx
基于数值微分和误差反向传播的比较
两种求梯度的方法:一种是基于数值微分的方法,另一种是于误差反向传播的方法,对于数值微分来说,它的计算非常耗费时间,但是它的优点就在于其实现起来非常简单,一般情况下,数值微分实现起来不太容易出错,而误差反向传播法的实现就非常复杂,且很容易出错,所以经常会此较数值微分和误差反向传播的结果(两者的结果应该是非常接近的),以确认我们书写的反向传播逻辑是正确的。这样的操作就称为梯度确认(gradientcheck)。
数值微分和误差反向传播这两者的比较误差应该是非常小的,实现代码具体如下:
from collections import OrderedDict class TwoLayerNet: def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01): # 初始化权重 self.params = {} self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)#W1 是第一层的权重矩阵,形状为 (input_size, hidden_size),即输入层到隐藏层的权重。np.random.randn(input_size, hidden_size) 生成一个正态分布(均值为0,标准差为1)的随机数矩阵,weight_init_std 是一个用于缩放的标准差,目的是控制初始权重的分布。 self.params['b1'] = np.zeros(hidden_size)#b1 是第一层的偏置向量,形状为 (hidden_size,),即对应隐藏层的偏置 self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b2'] = np.zeros(output_size) # 生成层 self.layers = OrderedDict() self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])#创建一个名为Affine1的全连接层(Affine Layer),并将其存储在self.layers字典中 self.layers['Relu1'] = Relu() self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2']) self.layers['Relu2'] = Relu() self.lastLayer = SoftmaxWithLoss() def predict(self, x): for layer in self.layers.values(): x = layer.forward(x) return x # x:输入数据, y:监督数据 def loss(self, x, y): p = self.predict(x) return self.lastLayer.forward(p, y) def accuracy(self, x, y): p = self.predict(x) p = np.argmax(y, axis=1) if y.ndim != 1 : y = np.argmax(y, axis=1) accuracy = np.sum(p == y) / float(x.shape[0]) return accuracy # x:输入数据, y:监督数据 def numerical_gradient(self, x, y): loss_W = lambda W: self.loss(x, y) grads = {} grads['W1'] = numerical_gradient(loss_W, self.params['W1']) grads['b1'] = numerical_gradient(loss_W, self.params['b1']) grads['W2'] = numerical_gradient(loss_W, self.params['W2']) grads['b2'] = numerical_gradient(loss_W, self.params['b2']) return grads def gradient(self, x, y): # forward self.loss(x, y) # backward dout = 1 dout = self.lastLayer.backward(dout) layers = list(self.layers.values()) layers.reverse()#执行这行代码后,layers列表中的层从最后一层到第一层排列。 for layer in layers: dout = layer.backward(dout) # 设定 grads = {} grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db return grads network = TwoLayerNet(input_size=784,hidden_size=50,output_size=10) x_batch = x_train[:100] y_batch = y_train[:100] grad_numerical = network.numerical_gradient(x_batch,y_batch) grad_backprop = network.gradient(x_batch,y_batch) for key in grad_numerical.keys(): diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) ) print(key + ":" + str(diff))#str()函数将diff转换为字符串形式,以便与key进行拼接
OrderedDict是有序,“有序”是指它可以“记住”我们向这个类里添加元素的顺序,因此神经网络的前装着只需要按照添加元素的顺序调用各层的Forward方法即可完成处理,而相对的误差编传播则只需要按照前向传播相反的顺序调用各层的backward 方法即可
通过反向传播实现 MNIST 识别
from collections import OrderedDict class TwoLayerNet: def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01): # 初始化权重 self.params = {} self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size) self.params['b1'] = np.zeros(hidden_size) self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b2'] = np.zeros(output_size) # 生成层 self.layers = OrderedDict() self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1']) self.layers['Relu1'] = Relu() self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2']) self.layers['Relu2'] = Relu() self.lastLayer = SoftmaxWithLoss() def predict(self, x): for layer in self.layers.values(): x = layer.forward(x) return x # x:输入数据, y:监督数据 def loss(self, x, y): p = self.predict(x) return self.lastLayer.forward(p, y) def accuracy(self, x, y): p = self.predict(x) p = np.argmax(p, axis=1) y = np.argmax(y, axis=1) accuracy = np.sum(y == p) / float(x.shape[0]) return accuracy def gradient(self, x, y): # forward self.loss(x, y) # backward dout = 1 dout = self.lastLayer.backward(dout) layers = list(self.layers.values()) layers.reverse() for layer in layers: dout = layer.backward(dout) # 设定 grads = {} grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db return grads
训练这个神经网络
train_size = x_train.shape[0] iters_num = 600 learning_rate = 0.001 epoch = 5 batch_size = 100 network = TwoLayerNet(input_size = 784,hidden_size=50,output_size=10) for i in range(epoch): print('current epoch is :', i) for num in range(iters_num): batch_mask = np.random.choice(train_size,batch_size) x_batch = x_train[batch_mask] y_batch = y_train[batch_mask] grad = network.gradient(x_batch,y_batch) for key in ('W1','b1','W2','b2'): network.params[key] -= learning_rate*grad[key] loss = network.loss(x_batch,y_batch) if num % 100 == 0: print(loss) print('准确率: ',network.accuracy(x_test,y_test) * 100,'%')
正则化惩罚
像某些特定的权重添加一些偏好,对其他权重则不添加。以此来消除模糊性。与权重不同,偏差没有这样的效果,因为它们并不控制输人维度上的影响强度。因此通常只对权重正则化,而不正则化偏差(bias)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号