java之类型转化

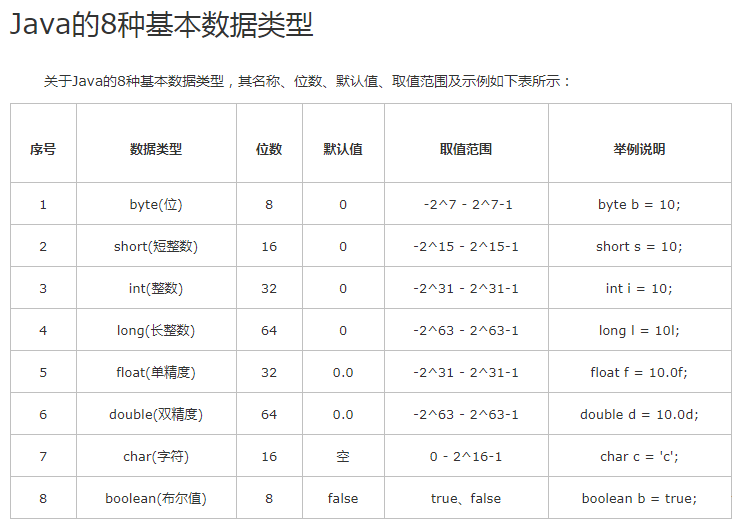
首先明确知道各个类型所占的字节：

1.比较空间大小：小空间变量不可以直接存储大空间的变量（需要强制类型转换），况且在转换过程中如果数值范围超过边界，可能会损失精度。例如：

int a = 1000; // 1000这个十进制转换成二进制是（转换公式是十进制除以2取余数，余数倒序排序就是二进制了） 00000000   00000000  00000011  11101000 

byte b = (byte) a;  // 编译跟执行都可以，不过就是会损失精度（byte类型最大只能储存127）

system.out.println(b)； //输出结果是-24    经过强制转换之后，计算机会砍掉00000000   00000000  00000011  11101000 中的00000000   00000000  00000011，只留下11101000

解析b的答案由来：首先b的二进制是：11101000，因为第一位是1表示负数，所以二进制负数转换成十进制的口诀是：

第一步：对二进制数逐位取反，11101000-》00010111

第二步：对取反后的二进制数加1，加上负号，结果就是二进制负数转化成的十进制数，00010111-》00011000，这个二进制转换成十进制就是2的三次方加上2的四次方等于24，最后加上符号-，结果是-24.

总结如下：计算机中，数值均以补码形式存储，正数的原码、反码、补码相同。负数的反码由原码符号位不变其余位取反求得，补码等于反码+1。

-------------------------

如果int a = 1; byte b = (byte) a; //这样就不会损失精度，输出b的结果就是1，以为1这个十进制转化成二进制是00000000 0000000 00000000 0000001（int类型是32位），砍掉前面24位不影响结果，也就是1

-------------------------------------------------------------------

2.比较精确程度：类型不一样，哪个精度程度高就转化成哪种，因为浮点型精确程度比int和long更高，可以直接存放，反之需要强制转换，不然就会报错

int a = 1; // 32bit

float b = a; // 32bit

system.out.println(b); // 输出结果是1.0

再一个例子就是：

long a = 1;// 64bit

float b = a; // 32bit

system.out.println(b)； //  输出是1.0

================================

最后摘录别人的总结如下：

所以欲把计算机存储的二进制转换为相应的十进制数值的一般步骤是：

1）先看这个数是有符号数还是无符号数，若是无符号/正数，则直接转化为十进制；

2）两种方法之一：若为负数，则存储的是补码，最高位不变，-1得到其反码，然后最高位不变，其余位全部取反得到原码，然后转化为十进制并添加负号。

两种方法之二：若为负数，则存储的是补码，最高位不变，其余位全部取反得到原码，+1得到其反码，然后转化为十进制并添加负号。

例:

有符号char类型值的负数部分在计算机中的实际存储状态(以补码形式)：

各种进制数的转换打印尤需注意：

例如：

最后需注意：有符号数的最高位为符号位，当二进制数值在原码、反码、补码相互转化时，取反动作均保持最高位不动，而任何情况引起的进位溢出可以改变最高位的1/0状态