计算机网络概论
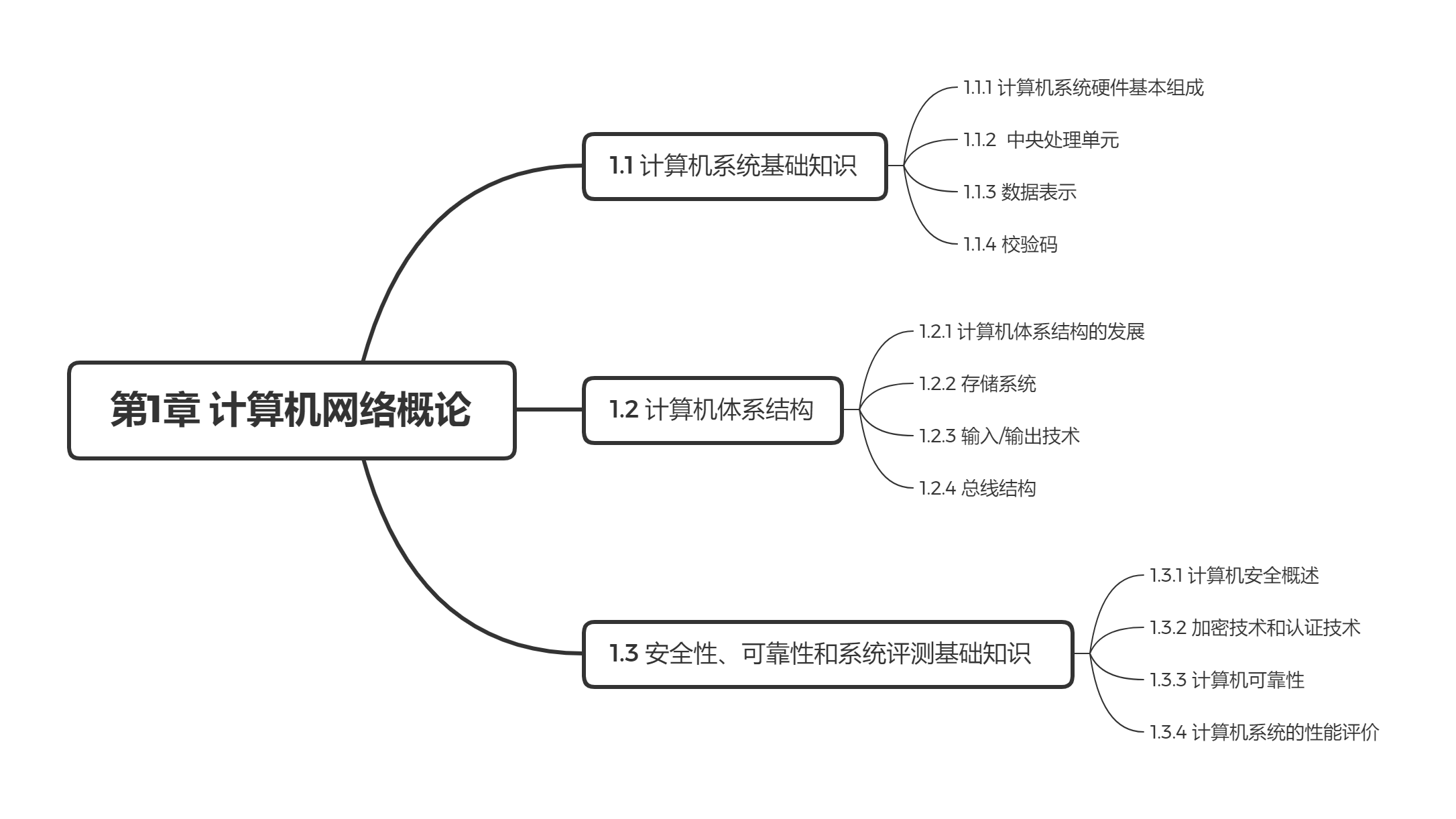
计算机网络概论为什么是由图1中给出的3部分组成?
-
编书者想让读者能了解到
- 计算机它内部有哪些东西?
- 计算机内部这些东西是怎么组合起来形成一个计算机的?
- 计算机作为帮助人们计算的工具会出错吗?帮助人们交流会泄密?能保证交流的对象是预想的人吗?
- 计算机好不好用?
-
计算机内部有哪些东西?
-
拿台式机来说,我们能看到主机、显示器、鼠标、键盘
完成一项工作,用计算机的概念来说就是输入->处理->输出,因此计算机的组件可以简单分成3部分。
- 输入:键盘、鼠标
- 输出:显示器
- 处理:主机
我们知道把程序(数据+算法)通过 键盘、鼠标 输入到主机,经过处理,得到结果,输出到显示器
-
主机在处理的时候又是依靠哪些部件的呢?
- CPU:完成具体工作的部分
- CPU是怎么完成工作的?
- 我们完成工作的时候有在时间上总有一个先后顺序,然后再开始完成X部分(最小工作单元)
- CPU同样需要一个控制器来知道先后顺序,然后再用运算器处理X部分
- CPU是怎么完成工作的?
- 存储器:存放工作需要的数据(资料),和工作的流程:a->b->c..
- CPU:完成具体工作的部分
-
总结:输入设备,主机【CPU(运算器、存储器)、存储器】,输出设备
-
-
计算机这种工具到底应该能帮助人类解决什么问题,所以要怎么设计?体系结构
-
由谁来干活?
-
一个屋子里一个人干活?单处理系统
-
一个屋子里多个人同时一起在干活?并行处理和多处理系统
-
多个屋子里的多个人一起干活?分布式系统
-
-
用什么方式干活?
- 怎么配置指令和数据?SISD、SIMD、MISD、MIMD
- 怎么配置工作时的处理并行度?WSBS、WPBS、WSBP、WPBP
- 怎么配置使用工具的并行度?处理机、算逻单元、逻辑门
-
-
计算机这种工具内部的部分应该怎么互相关联,最终组成一个计算机?组成原理
-
计算机这种工具内部的部分应该用哪些器件来实现?实现
CPU(中央处理器)
-
1.知道工作的步骤 控制器 2.完成具体部分工作 运算器
-
控制器=程序控制+操作控制+时间控制+中断处理=控制执行指令,执行时间,执行部件,处理异常
- 指令寄存器IR:PC发现该执行a指令了,把a指令从内存捞到DR,指令译码器ID解析IR的a指令,完成a指令的内容
- 程序计数器PC:寄存信息-指令,计数-知道下步该指向哪个位子(顺序执行=n+1,转移执行=n+位移量)
- 地址寄存器AR:保存当前CPU访问的内存地址的信息,CPU和内存操作速度差别大,所以要留个位置,好知道内存的读/写操作完成了没有。
- 指令译码器ID:解析指令。指令=操作码+地址码。ID就是对操作码翻译,向操作控制器发出控制信号。
- 时序逻辑:按该逻辑发送每条指令执行时间点的控制信号
- 总线逻辑:处理多个部件通过总线完成各种交流。
- 中断控制逻辑:处理中断请求,按优先级排序再交给CPU处理
-
运算器=数据处理=加减乘除及附加运算,执行所有的逻辑运算
- 算术逻辑单元ALU:算术运算和逻辑运算
- 累加器AC:通用寄存器,为ALU服务,提供一个工作区,暂时存放数据和结果
- 数据缓冲寄存器DR:为CPU从内存储器读/写指令或数据服务
- 状态条件寄存器PSW:为ALU的服务,记住ALU运算的一个标志
-
运算器和控制器中的寄存器都是专用寄存器,作用固定。通用寄存器用途广泛,可自定义其用途。
数据表示
码制:原码、反码、补码、移码
数据类型:定点整数,定点小数,浮点数
-
为什么需要四种码制?
原码:二进制表示
反码:多应用于系统环境设置,如linux平台的目录和文件的默认权限的设置umask,就是使用反码原理
补码:使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理
移码:又叫增码或偏置码,方便表示浮点数的阶码
-
为什么需要三种数据类型?
和现实的数相对应
校验码
奇偶校验码PC、海明码HC、循环冗余校验码CRC
-
为什么需要校验码?
计算机系统传输数据时,可以抽象都是一串二进制数,在硬件上就是开或关两种状态,一种物理状态。因此实际上我们在接收信息的时候,希望信息在硬件上的传输过程是可靠的。校验码就是为了检验信息传输的可靠性。
-
校验码:百度百科-校验码
-
奇偶校验码:
- 一串代码:11010010
- 信息位:1101001, 校验位 C:0
- 校验位算法:1.奇校验 \(P=\overline{X_1\bigoplus X_2\bigoplus X_3...X_n}\) 2.偶校验 \(P=X_1\bigoplus X_2\bigoplus X_3...X_n\)
- 有效性算法:1.\(G=\overline{C\bigoplus {X_1\bigoplus X_2\bigoplus X_3...X_n}}\) 2.\(G=C\bigoplus {X_1\bigoplus X_2\bigoplus X_3...X_n}\)
- 结果:1. \(P=1,C=0,G=1\) 2.\(P=0,C=0,G=0\)
- 有效性:1. \(P\neq C,G\neq0\),2. \(P=C,G=0\),1.奇校验出现了奇数个错误,2.偶校验正确或者出了偶数个错误。
- 为什么说是奇数个错误?
- 因为,当出现偶数个错误的时候结果和正确性一致,可以理解为负负得正
-
循环冗余校验码:CRC码计算及校验原理的最通俗诠释


 浙公网安备 33010602011771号
浙公网安备 33010602011771号