DS博客作业02--线性表
0.PTA得分截图

1.本周学习总结
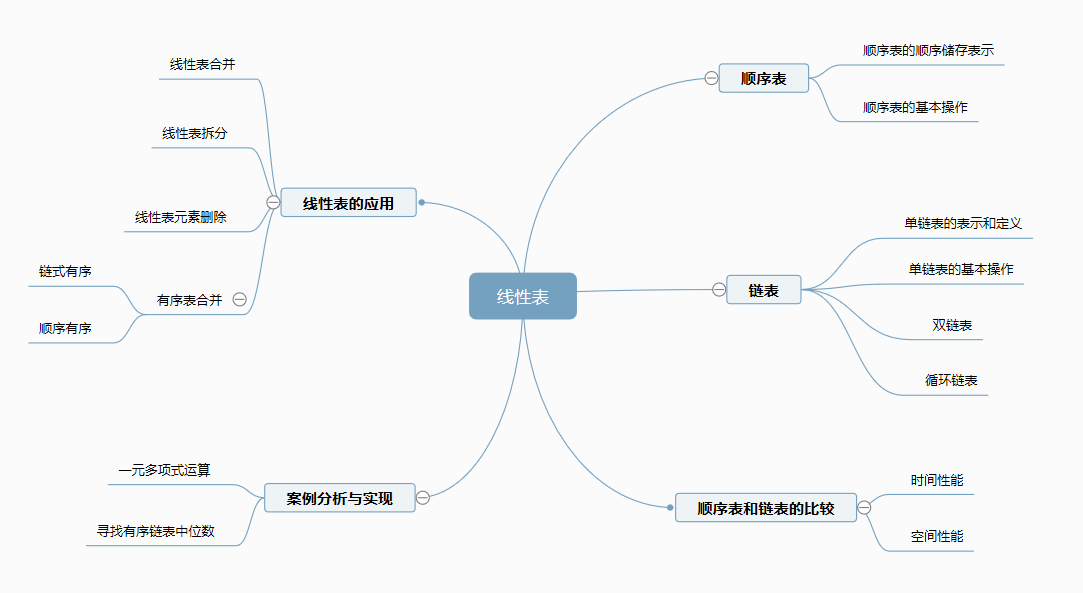
1.1 总结线性表内容
1.1.1顺序表
顺序表结构体定义
typedef int ElemType; //重命名int类型为ElemType,方便后续数据类型更改
typedef struct
{
ElemType data[MaxSize]; //存放顺序表元素
int length ; //存放顺序表的长度,也可写成int last(数组最后元素下标)
} List,*SqList;
顺序表插入
void InsertSq(SqList &L,int x) //有序插入数据x
{
int i,j;
for (i = 0; i < L->length; i++)
{
if (x < L->data[i]) //找到插入位置
{
for (j = L->length - 1; j >= i; j--) //数据右移一位
{
L->data[j + 1] = L->data[j];
}
L->data[i] = x; //插入数据
L->length++; //顺序表长度加一
break;
}
}
if (i == L->length) //插入数据在表尾
{
L->length++;
L->data[i]=x;
}
}
顺序表删除
void DelNode(List& L,int x) //删除顺序表中值为X的数据
{
int j,k;
for (j = 0; j < L->length; j++)
{
if (L->data[j] == x) //找到数据位置
{
for (k = j; k < L->length; k++)
{
L->data[k] = L->data[k + 1];
}
L->length--;//表长度减一
i--;//长度减一时i减1,防止跳过数据
}
}
}
顺序表查找
int SerchNode(List L,int i)//查找顺序表第i个元素
{
return L->data[i]//顺序表的随机存取特性
}
1.1.2链表
链表结构体定义
typedef struct LNode //定义单链表结点类型
{
ElemType data;
struct LNode *next; //指向后继结点
} LNode,*LinkList; //重新命名结构体指针类型为LinkList
头插法
void CreateListF(LinkList& L, int n)//建立长度n的链表
{
L = new LNode;
L->next = NULL;
LinkList p;
if (n == 0)//空链
{
cout << "空链表!" << endl;
}
for (n ; n > 0 ; n--)//头插法建链
{
p = new LNode;
cin >> p->data;
p->next = L->next;
L->next = p;
}
}
尾插法
void CreateListR(LinkList& L, int n)//建立长度n的链表
{
LinkList tail ,p;
tail = new LNode;//尾指针
L = new LNode;
L->next = NULL;
tail = L;
for (n ; n > 0 ; n--)//尾插法建链表
{
p = new LNode;
tail->next = NULL;//尾指针next域为空
cin >> p->data;
tail->next = p;
tail = p;
}
}
链表插入
void ListInsert(LinkList& L, ElemType e)//有序链表插入元素e
{
LinkList pre,p;
p = new LNode;
p->data = e;
pre = L;//前驱指针
while (pre->next && pre->next->data < e)//寻找插入位置的前驱
{
pre = pre->next;
}
p->next = pre->next;//插入
pre->next = p;
}
链表删除
void ListDelete(LinkList& L, ElemType e)
{
LinkList pre=L;
if (L->next == NULL) return;//空链直接返回
while(pre->next)//寻找删除位置的前驱
{
if (pre->next->data == e)//删除
{
pre->next = pre->next->next;
return;
}
pre = pre->next;
}
cout << e << "找不到!"<< endl;
}
链表查找
int GetList(LinkList L,int n) //查找第n个数
{
LinkList p;
int i;
p=L;
for(i=0;i<n;i++)
{
p=p->next;
}
return p->data;
}
链表销毁
void DestroyList(LinkList &L)
{
LinkList p = L;
while (L)
{
p = L;
L = L->next;
delete p;
}
}
1.1.3有序表
有序单链表数据插入
void ListInsert(LinkList& L, ElemType e)//有序链表插入元素e
{
LinkList pre,p;
p = new LNode;
p->data = e;
pre = L;//前驱指针
while (pre->next && pre->next->data < e)//寻找插入位置的前驱
{
pre = pre->next;
}
p->next = pre->next;//插入
pre->next = p;
}
有序单链表数据删除
void ListDelete(LinkList& L, ElemType e)
{
LinkList pre=L;
if (L->next == NULL) return;//空链直接返回
while(pre->next)//寻找删除位置的前驱
{
if (pre->next->data == e)//删除
{
pre->next = pre->next->next;
return;
}
pre = pre->next;
}
cout << e << "找不到!"<< endl;
}
有序表合并
方法一:
void MergeList(LinkList& L1, LinkList L2)
{
LinkList p = L1->next, q = L2->next,tail;
L1->next = NULL;
tail = L1;
while (p && q)
{
if (p->data < q->data)
{
tail->next = p;
tail = p;
p = p->next;
}
else if (p->data > q->data)
{
tail->next = q;
tail = q;
q = q->next;
}
else
{
tail->next = p;
tail = p;
p = p->next;
q = q->next;
}
}
if (p)
{
tail->next = p;
}
if (q)
{
tail->next = q;
}
}
方法二:
void MergeList(LinkList& L1, LinkList L2)
{
LinkList p ,pre;
pre=L1;
while(pre->next&&L2->next)
{
if(pre->next->data>L2->next->data)
{
p=new LNode;//若不申请内存,PTA运行超时
p->data=L2->next->data;
p->next=pre->next;
pre->next=p;
L2=L2->next;
}
else if(pre->next->data==L2->next->data)
{
L2=L2->next;
}
pre=pre->next;
}
if(pre->next==NULL)
{
pre->next=L2->next;
}
}
1.1.3循环链表
-
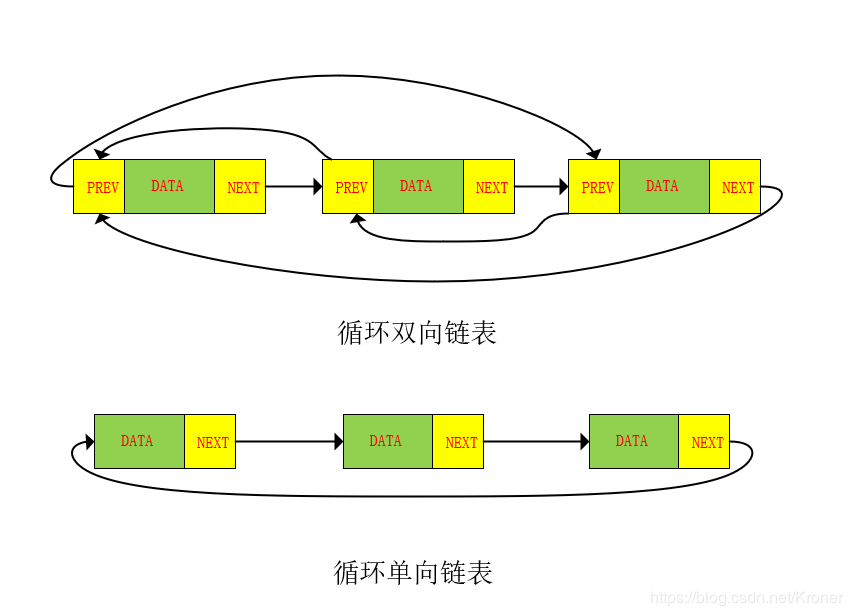
下图为循环链表的主要两种类型。
![]()
-
循环链表是指尾结点和头结点相连形成环状的链表,在建立一个循环链表时,必须使其最后一个结点的指针指向表头结点,而不是象单链表那样置为NULL。此种情况还使用于在最后一个结点后插入一个新的结点。
-
循环链表可以从任意结点找到目标结点,这是循环链表的优点与特点。
-
带头结点的循环链表遍历一遍结束条件为p->next=head。
1.1.4双链表
-
双向链表也叫双链表,是链表的一种,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。
![]()
-
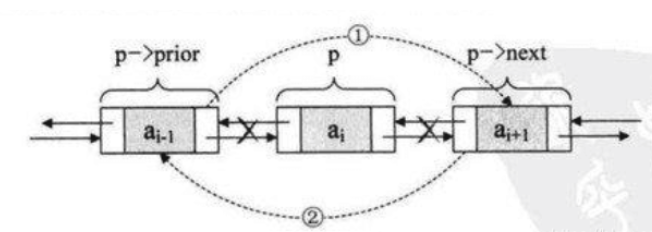
双链表删除
![]()
p->prior->next=p->next;
p->next->prior=p->prior;
delete(p);
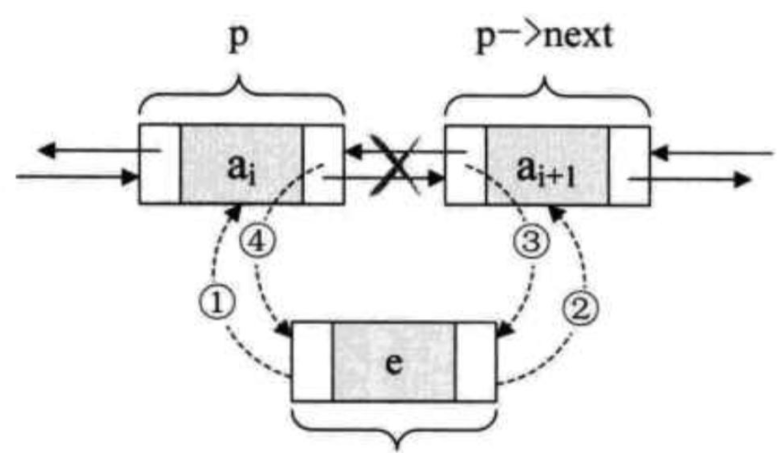
- 双链表插入
![]()
s->prior=p;
s->next=p->next;
p->next->prior=s;
p->next=s;
1.2.谈谈你对线性表的认识及学习体会。
- 在学习数据结构第二章线性表的内容之后,觉得数据结构的内容比较抽象,理解起来有一定的难度,经常看代码时明白而后容易遗忘。
- 这部分内容编程起来指针使用比较多,一旦产生错误容易无从下手不知道问题出错在哪。
- 解体思路往往不止一种,而多种思路就容易产生混乱,写出来的代码在效率上也明显存在差异,做新思路的代码填空题也是比较有难度的。
- 操作线性表时经常遇到指针非法访问内存这一问题,主要原因是空指针进行了next操作或是指针定义时没有初始化为空指针。
- 链表遍历或是进行各种操作前应该先考虑链表是否为空,这个经常也是PTA的测试点,或是一些特殊情况的出现的原因。
2.PTA实验作业
2.1.题目1:链表倒数第m个数
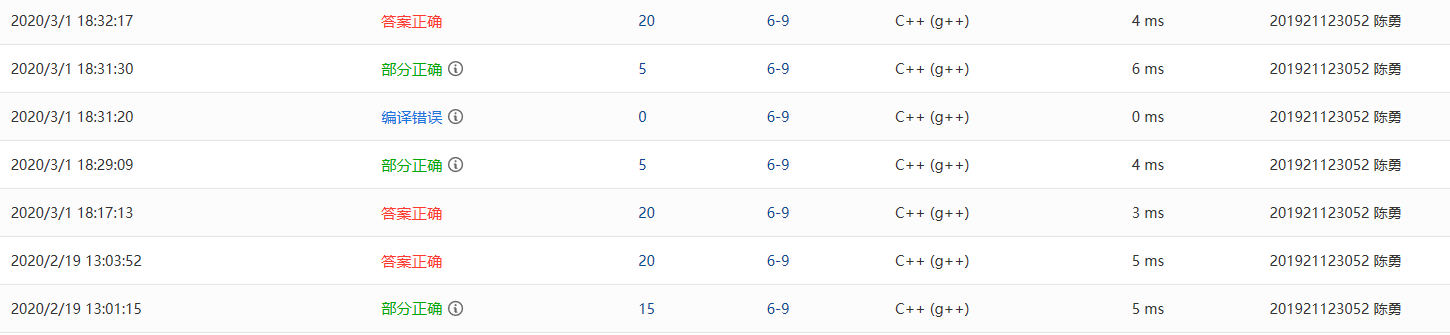
2.1.1代码截图
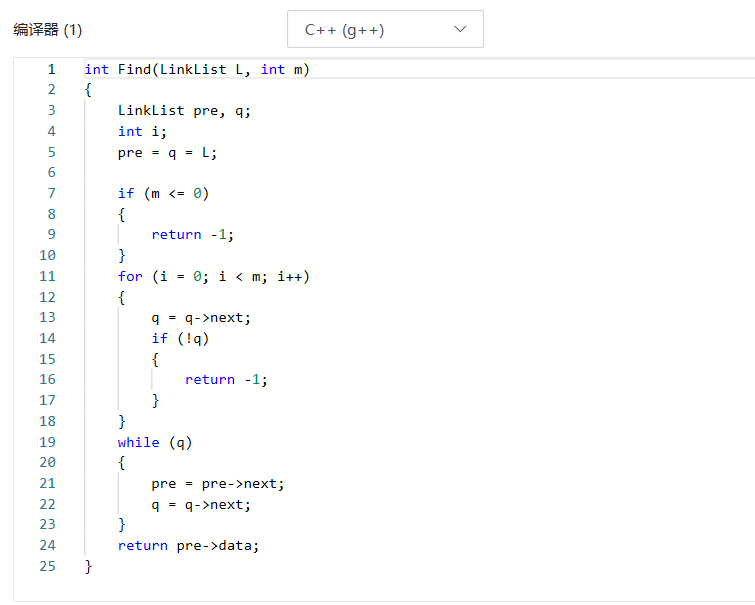
2.1.2本题PTA提交列表说明。
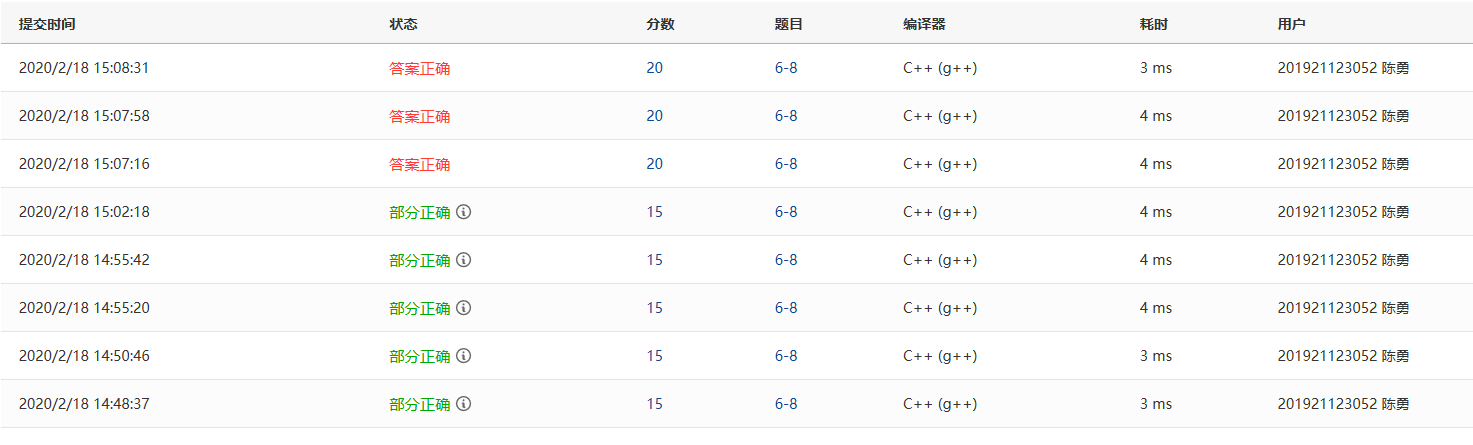
- Q:前两个部分错误是因为考虑倒数第m个数位置无效不全面,即m的取值范围没有考虑周到
- A:先判断m的范围,若不正确则直接返回。
- Q:后面的部分错误是因为在链表遍历上的快指针为空的情况没有考虑到。
- A:在快指针移动时,判断指针是否为空,若为空则直接返回。
- 最后答案正确试了另一种方法。
2.2 题目2:有序链表的插入删除
2.2.1代码截图
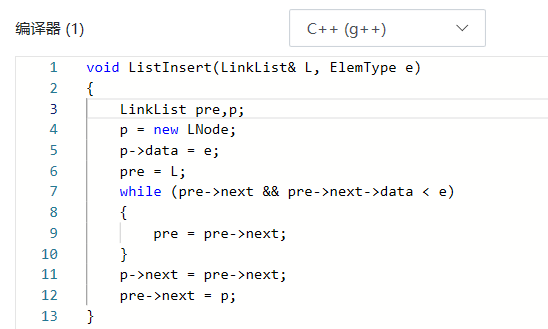

2.2.2本题PTA提交列表说明。

- Q:第一次部分正确是因为删除时没有考虑链表为空的情况,导致链表全删除时输出错误。
- A:先判断链表是否是空链,若是空链直接返回。
- Q:第二次部分正确是由于找不到和空链表的情况下输出冲突,当链表为空时多输出了一句“找不到”。
- A:在循环下加入return
2.3 题目3:有序链表合并
2.3.1代码截图

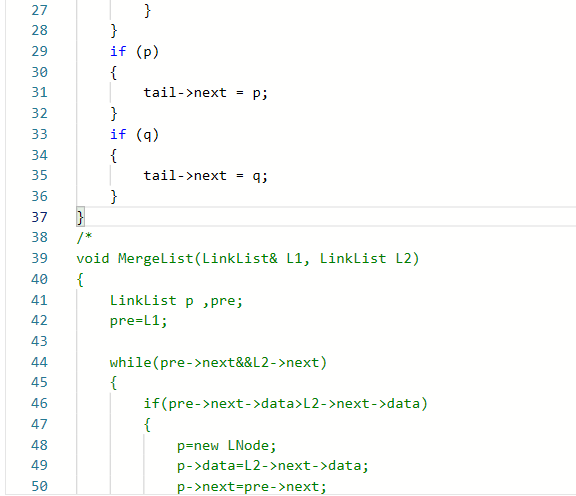

2.3.2本题PTA提交列表说明。
解法一:
- Q:第一次部分正确是第一种做法时,重复数据没有删除。
- A:增加else判断数据元素相等时的情况,即写入一个数据后两个指针同时移动。
解法二:
- Q:部分正确最后没有判断pre->next==NULL的情况。
- Q:编译错误是从VS上复制错误。
3.阅读代码
注意:不能选教师布置在PTA的题目。完成内容如下。
3.1 判断一个单链表中是否有环
核心代码:

完整代码:

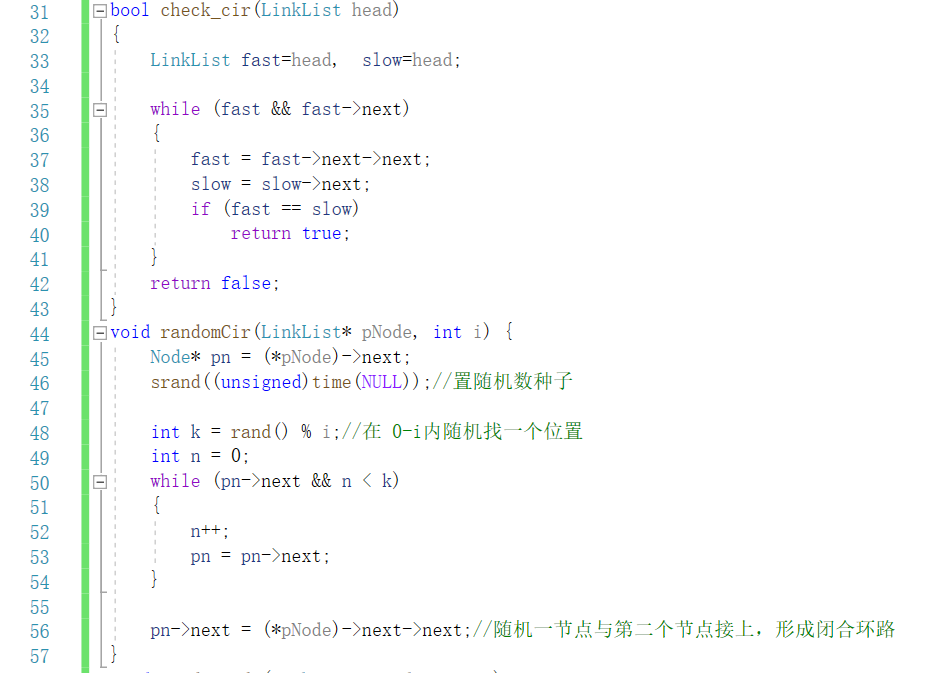

3.1.1 该题的设计思路
用两个指针去遍历,一个指针一次走两步,一个指针一次走一步,如果有环,两个指针肯定会在环中相遇,即采用“快慢指针”的方法,就是有两个指针fast和slow,开始的时候两个指针都指向链表头head,然后在每一步操作中slow向前走一步而fast每一步向前两步。由于fast要比slow移动的快,如果有环,fast一定会先进入环,而slow后进入环。当两个指针都进入环之后,经过一定步的操作之后二者一定能够在环上相遇,并且此时slow还没有绕环一圈,也就是说一定是在slow走完第一圈之前相遇。
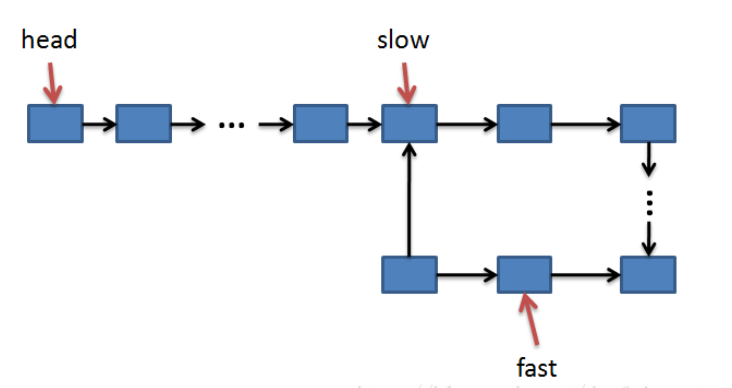
T(n)=O(n)
S(n)=O(1)
3.1.2 该题的伪代码
定义快慢指针fast slow都指向头结点;
while(fast&&fast->next)
{
快指针移动两步;
慢指针移动一步;
if(慢指针==快指针)
return true;
}
return false;
3.1.3 运行结果
测试一(不随机生成一个环):

运行结果:

测试二(随机产生一个环):

运行结果:

3.1.4分析该题目解题优势及难点。
- 首先要明确链中有环会出现的现象,如果一个链表中有环,也就是说用一个指针去遍历,是永远走不到头的。
- 避免理解错误,即单链表有环不一定是循环链表,因此判断指针p->next==Head的方法不适用于判断单链表是否有环。
- 该解法巧妙运用快慢指针快慢能相遇,则说明指针进入了环。
3.2 约瑟夫问题,又名约瑟夫斯问题(Josephus Problem)
描述如下:
N个人围成一圈,从第一个开始报数,第M个将被杀掉,最后剩下一个,其余人都将被杀掉。例如N=6,M=5,被杀掉的顺序是:5,4,6,2,3,1。
现在写出程序,要求输出顺序序列,且采用模拟法。
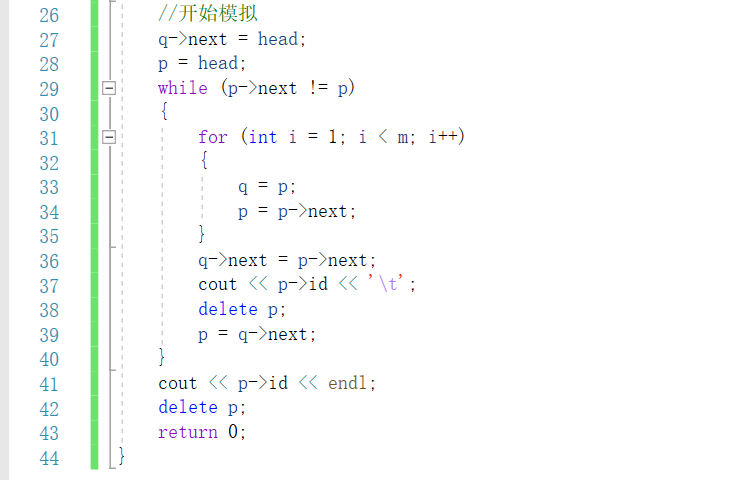
3.2.1该题的设计思路
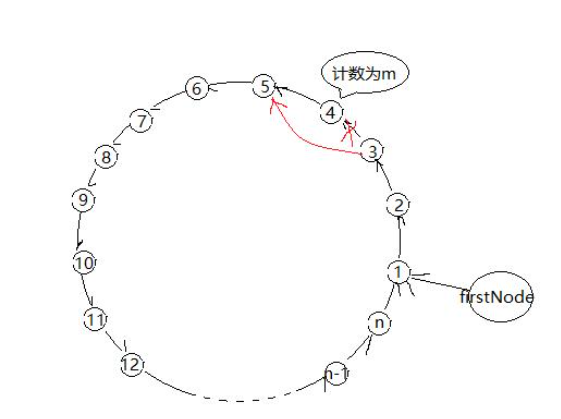
采用循环链表表示队列,当遍历到m的前驱时删除m,直到只剩下一个数据元素。
T(n)=O(nm)
S(n)=O(1)
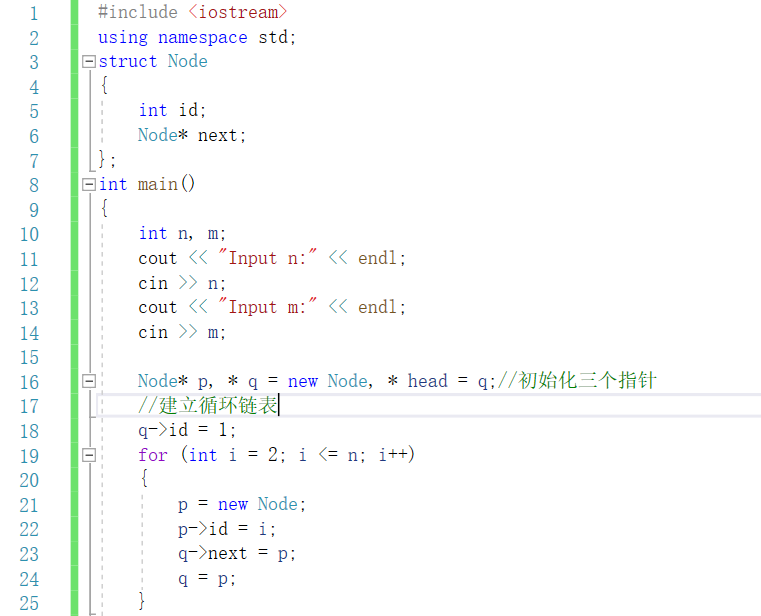
3.2.2该题的伪代码
输入n,m;
建立结点个数为n的循环单链表;
while(链中结点多于一个)
{
for (i = 1; i < m; i++) //遍历链表找到到第m个
{
q = p; //q为p的前驱
p = p->next;
}
输出p结点的序号;
删除结点p;
p=q->next;
}
cout << p->id << endl;//输出最后一个幸存者序号
删除结点p;
3.2.3运行结果
测试一:
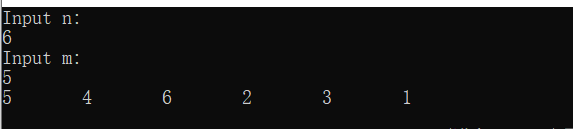
测试二:

3.1.4分析该题目解题优势及难点。
- 本题要先明确题目中数据的表示方法,题目中的人围成一圈,巧妙运用一个循环的链来表示,清楚的表示了数据直接的关系。
- 第m个人出列,在链表中就找到该结点的前驱指针,删除该结点,这是对循环链表遍历和删除的操作。
- 要明确找到循环结束的条件,即判断条件p->next==p是否成立,即最后只剩一个人时结束循环。
- 若不采用模拟法且直接输出幸存者号数,则可以根据递推关系经过数学计算,根据公式得出结果,且在时间上更加高效T(n)=O(n),如图:
![]()





 浙公网安备 33010602011771号
浙公网安备 33010602011771号