2023 ICPC Macau Regional Contest

A. (-1,1)-Sumplete  (思维 + 贪心)

https://codeforces.com/gym/104891/problem/A

https://www.cnblogs.com/yangqingli/p/4735607.html(模仿的格式)

题意:

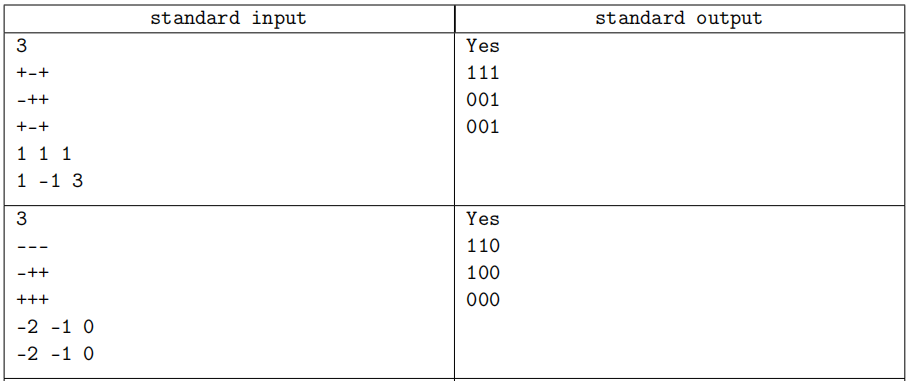
给你一个n*n(n<=4000)的矩阵,每个字符为'+'或者'-'， sij='+'表示aij可以填0或1，‘-’表示可以填0或-1。现给出你第i(1<=i<=n)行的和ri以及第j(1<=j<=n)列的和,现需要你给出一个合法填数方案(如果存在)。若不存在则输出No,存在则给出一个合法方案。

---

 

解法:

这道题是一道经典的思维题。

 我们先考虑将该问题简化:如果所有的sij='+'，这道题该怎么处理呢?

我们不难发现对于每一行，我们使用贪心选取最大的cj，然后在第j列填上一个1即可。可以证明如果存在解则该方案一定合法。

 

那么我们如何将问题简化成上述情况呢? 关键是如何将 -1 0两个选项转化为1 0 。

仔细观察我们可以发现，如果对于-1 0各自加1，则能将其转化为0 1。

 

于是我们成功地将问题转化为了上述情况。 

---

代码:

#include<bits/stdc++.h>
using namespace std;
const int N=4e3+5;
int n,r[N],c[N];
bool op[N][N];//op=1表示修改了
char s[N][N];
struct node{
    int id,x;
}a[N];
bool cmp(node b,node c){
    return b.x>c.x;
}
bool ans[N][N];
int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++)scanf("%s",s[i]);
    int sum=0;
    for(int i=0;i<n;i++)scanf("%d",&r[i]),sum+=r[i];
    for(int i=0;i<n;i++)scanf("%d",&c[i]),sum-=c[i];
    if(sum){
        puts("No");
        return 0;
    }
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            if(s[i][j]=='-')op[i][j]=1,r[i]++,c[j]++;
        }
    }
    int ok=1;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++)a[j].id=j,a[j].x=c[j];
        sort(a,a+n,cmp);
        for(int j=0;j<r[i];j++){
            if(a[j].x){
                c[a[j].id]--;
                ans[i][a[j].id]=1;
            }
            else {
                ok=0;
                puts("No");
                return 0;
            }
        }
    }
    puts("Yes");
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++)printf("%d",ans[i][j]^op[i][j]);
        puts("");
    }
    return 0;
}

 

　　

---

 H题:Random Tree Parking

题意:https://codeforces.com/gym/104891/problem/H

 

---

输入样例:

input
15
1 2 2 2 2 3 3 2 7 7 3 10 3 13
output: 938578089

 

---

题解:

这道题其实不怎么难(顶天Cu中下难度)，就是一个一般的树形DP f(i,j), j表示往上走的个数。

考试的时候没做出来是因为没看到"tree T should be generated randomly",导致我不敢写。

所以考试时应当用笔把重点限制条件勾画出来(也要多做题明白哪些是重点条件)。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
const int M=46;//  最大dep>=M概率<=0.001 
const ll mod=998244353;    
int n,dep[N];//dep+1
struct edges{
    int v,nxt;
}e[N];
int head[N],cnt;
void addedge(int u,int v){
    e[++cnt].v=v;e[cnt].nxt=head[u];head[u]=cnt;
}
ll f[N][M];//i j(还有j-1个点在上面)
ll pw(ll x,ll y){
    if(y==0)return 1;
    ll t=pw(x,y/2);
    t=t*t%mod;
    if(y%2)t=t*x%mod;
    return t;
} 
ll invfac[N],fac[N];
void init(){
    fac[0]=1;invfac[0]=1;
    for(ll i=1;i<N;i++){
        fac[i]=fac[i-1]*i%mod;
        invfac[i]=pw(fac[i],mod-2)%mod;
    }
}
void input(){
    scanf("%d",&n);
    int x;
    for(int i=2;i<=n;i++){
        scanf("%d",&x);
        addedge(x,i);
    }
}
ll g[N][M];

void dfs(int u,int fa){
    dep[u]=dep[fa]+1;
    for(int i=0;i<=dep[u];i++)f[u][i]=invfac[i];
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].v;
        if(v==fa)continue;
        dfs(v,u);
        for(int j=dep[u];j>=0;j--){
            for(int k=min(j,dep[v]);k>=0;k--){//设置临时数组避免重复计算 
                g[u][j]+=f[u][j-k]*f[v][k+1]%mod;
                continue;
            }
            f[u][j]=g[u][j]%mod;g[u][j]=0;
        }
    }
}
int main(){
    init();input();
    dep[0]=0; 
    dfs(1,0);
    cout<<f[1][1]*fac[n]%mod<<endl;
    return 0;
}