python3中的heapq模块使用
heapq-堆排序算法
heapq实现了一个适合与Python的列表一起使用的最小堆排序算法。
二叉树
树中每个节点至多有两个子节点

满二叉树
树中除了叶子节点,每个节点都有两个子节点
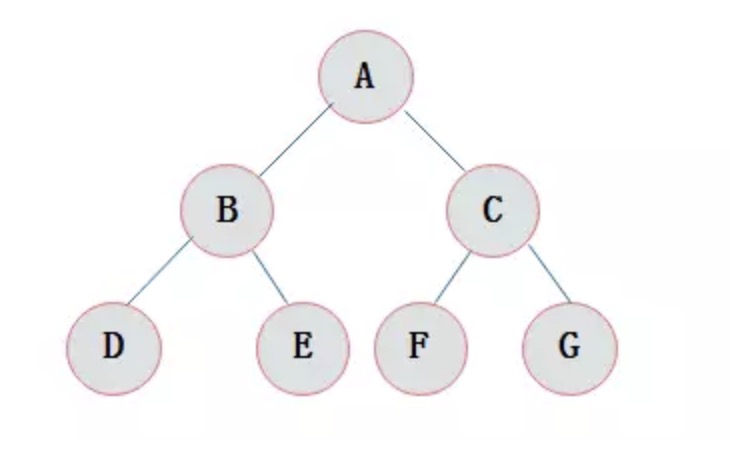
什么是完全二叉树
在满足满二叉树的性质后,最后一层的叶子节点均需在最左边
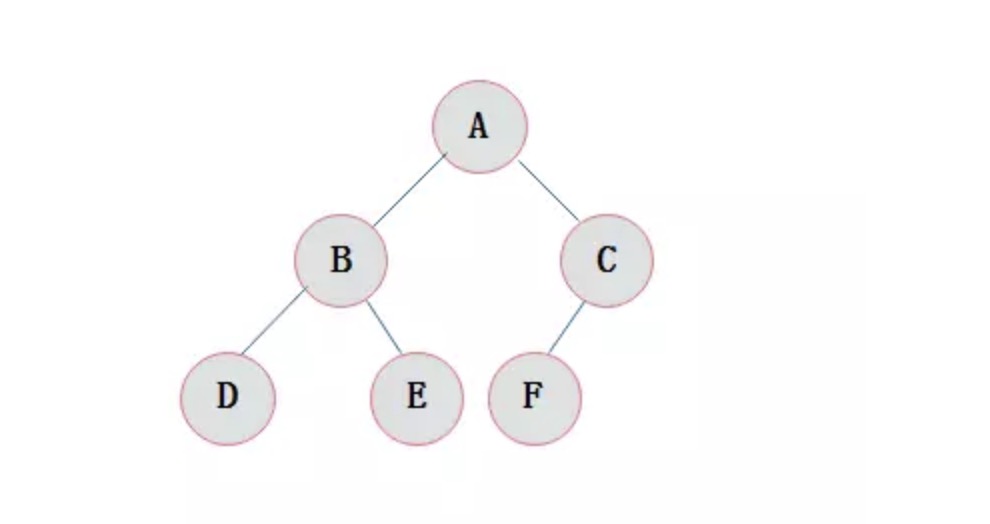
什么是堆?
堆是一种数据结构,它是一颗完全二叉树。最小堆则是在堆的基础增加了新的规则,它的根结点的值是最小的,而且它的任意结点的父结点的值都小于或者等于其左右结点的值。因为二进制堆可以使用有组织的列表或数组来表示,所以元素N的子元素位于位置2 * N + 1和2 * N + 2。这种布局使重新安排堆成为可能,因此在添加或删除项时不需要重新分配那么多内存
区分堆(heap)与栈(stack):堆与二叉树有关,像一堆金字塔型泥沙;而栈像一个直立垃圾桶,一列下来。
最大堆
最大堆确保父堆大于或等于它的两个子堆。
最小堆
最小堆要求父堆小于或等于其子堆。Python的heapq模块实现了一个最小堆。
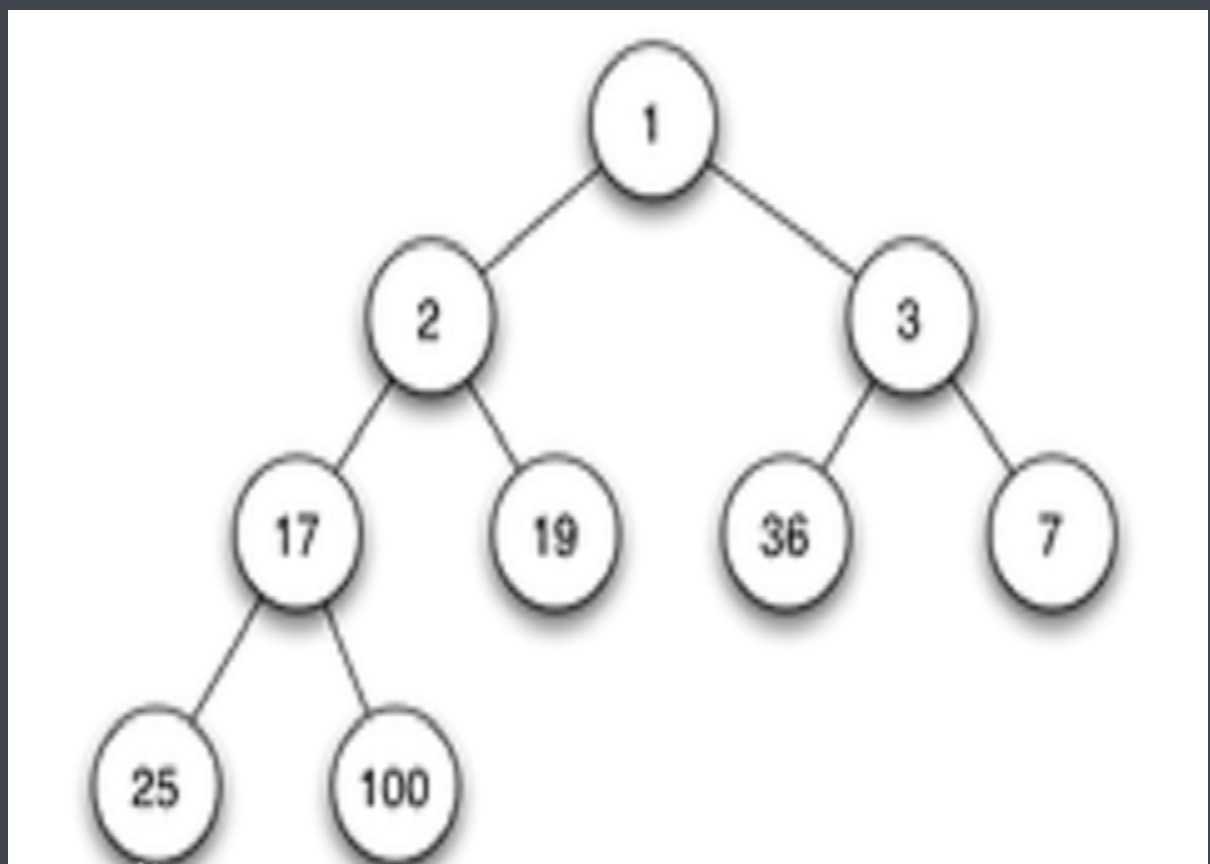
创建一个堆
示例代码:
heapq_heapdata.py
# This data was generated with the random module.
data = [19, 9, 4, 10, 11]
堆输出使用heapq showtree.py打印。
heapq_showtree.py
import math
from io import StringIO
def show_tree(tree, total_width=36, fill=' '):
"""Pretty-print a tree."""
output = StringIO()
last_row = -1
for i, n in enumerate(tree):
if i:
row = int(math.floor(math.log(i + 1, 2)))
else:
row = 0
if row != last_row:
output.write('\n')
columns = 2 ** row
col_width = int(math.floor(total_width / columns))
output.write(str(n).center(col_width, fill))
last_row = row
print(output.getvalue())
print('-' * total_width)
print()
这里有两种方案创建一个堆,一种是使用heappush(),一种是使用heapify()。
heappush
heapq_heappush.py
import heapq
from heapq_showtree import show_tree
from heapq_heapdata import data
heap = []
print('random :', data)
print()
for n in data:
print('add {:>3}:'.format(n))
heapq.heappush(heap, n)
show_tree(heap)
使用heappush()时,当从数据源添加新项时,将维护元素的堆排序顺序。
python3 heapq_heappush.py
random : [19, 9, 4, 10, 11]
add 19:
19
------------------------------------
add 9:
9
19
------------------------------------
add 4:
4
19 9
------------------------------------
add 10:
4
10 9
19
------------------------------------
add 11:
4
10 9
19 11
------------------------------------
如果数据已经在内存中,那么使用heapify()重新排列列表中的项会更有效。
heapify
heapq_heapify.py
import heapq
from heapq_showtree import show_tree
from heapq_heapdata import data
print('random :', data)
heapq.heapify(data)
print('heapified :')
show_tree(data)
按照堆顺序每次构建一项列表的结果与构建无序列表然后调用heapify()相同。
$ python3 heapq_heapify.py
random : [19, 9, 4, 10, 11]
heapified :
4
9 19
10 11
------------------------------------
访问堆的内容
使用heappop()弹出并返回堆中的最小项,保持堆不变。如果堆是空的,则引发IndexError。
heapq_heappop.py
import heapq
from heapq_showtree import show_tree
from heapq_heapdata import data
print('random :', data)
heapq.heapify(data)
print('heapified :')
show_tree(data)
print()
for i in range(2):
smallest = heapq.heappop(data)
print('pop {:>3}:'.format(smallest))
show_tree(data)
在本例中,使用heapify()和heappop()用于对数字列表进行排序。
$ python3 heapq_heappop.py
random : [19, 9, 4, 10, 11]
heapified :
4
9 19
10 11
------------------------------------
pop 4:
9
10 19
11
------------------------------------
pop 9:
10
11 19
------------------------------------
要删除现有元素并用单个操作中的新值替换它们,请使用heapreplace()。
heapreplace
heapq_heapreplace.py
import heapq
from heapq_showtree import show_tree
from heapq_heapdata import data
heapq.heapify(data)
print('start:')
show_tree(data)
for n in [0, 13]:
smallest = heapq.heapreplace(data, n)
print('replace {:>2} with {:>2}:'.format(smallest, n))
show_tree(data)
替换适当的元素可以维护固定大小的堆,比如按优先级排序的作业队列。
$ python3 heapq_heapreplace.py
start:
4
9 19
10 11
------------------------------------
replace 4 with 0:
0
9 19
10 11
------------------------------------
replace 0 with 13:
9
10 19
13 11
------------------------------------
堆中的数据极端值
heapq还包含两个函数,用于检查一个迭代器,并找到它所包含的最大或最小值的范围。
heapq_extremes.py
import heapq
from heapq_heapdata import data
print('all :', data)
print('3 largest :', heapq.nlargest(3, data))
print('from sort :', list(reversed(sorted(data)[-3:])))
print('3 smallest:', heapq.nsmallest(3, data))
print('from sort :', sorted(data)[:3])
使用nlargest()和nsmallest()仅对n> 1的相对较小的值有效,但在少数情况下仍然可以派上用场。
$ python3 heapq_extremes.py
all : [19, 9, 4, 10, 11]
3 largest : [19, 11, 10]
from sort : [19, 11, 10]
3 smallest: [4, 9, 10]
from sort : [4, 9, 10]
有效地合并排序Sequences
对于小数据集来说,将几个排序的序列组合成一个新的序列是很容易的。
list(sorted(itertools.chain(*data)))
对于较大的数据集,这种技术可以使用相当大的内存。merge()不是对整个组合序列进行排序,而是使用堆每次生成一个新序列中的一个项,并使用固定数量的内存确定下一个项。
heapq_merge.py
import heapq
import random
random.seed(2016)
data = []
for i in range(4):
new_data = list(random.sample(range(1, 101), 5))
new_data.sort()
data.append(new_data)
for i, d in enumerate(data):
print('{}: {}'.format(i, d))
print('\nMerged:')
for i in heapq.merge(*data):
print(i, end=' ')
print()
因为merge()的实现使用堆,所以它根据要合并的序列的数量而不是这些序列中的项的数量来消耗内存。
$ python3 heapq_merge.py
0: [33, 58, 71, 88, 95]
1: [10, 11, 17, 38, 91]
2: [13, 18, 39, 61, 63]
3: [20, 27, 31, 42, 45]
Merged:
10 11 13 17 18 20 27 31 33 38 39 42 45 58 61 63 71 88 91 95
上面是小根堆的相关操作。python的heapq不支持大根堆,在stackoverflow上看到了一个巧妙的实现:我们还是用小根堆来进行逻辑操作,在做push的时候,我们把最大数的相反数存进去,那么它的相反数就是最小数,仍然是堆顶元素,在访问堆顶的时候,再对它取反,就获取到了最大数。思路很是巧妙。下面是实现代码
class BigHeap:
def init(self):
self.arr = list()
def heap_insert(self, val):
heapq.heappush(self.arr, -val)
def heapify(self):
heapq.heapify(self.arr)
def heap_pop(self):
return -heapq.heappop(self.arr)
def get_top(self):
if not self.arr:
return
return -self.arr[0]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号