随笔分类 - 数论——矩阵
摘要:题面 "传送门" 题解 先考虑全都放$1\times 2$的方块的方案,设防$i$列的方案数为$g_i$,容易推出$g_i=g_{i 1}+g_{i 2}$,边界条件为$g_0=g_1=1$ 然后设$f_i$表示可以放$1\times 1$方块的方案。如果最右边一列不放$1\times 1$,那么转
阅读全文
摘要:"传送门" 又炸了…… $A$ 唐时月夜 不知道改了什么东西之后就$A$掉了$.jpg$ 首先,题目保证“如果一片子水域曾经被操作过,那么在之后的施法中,这片子水域也一定会被操作” 这个意思就是说,如果一个点$(x,y)$被操作过,那么它被进行的操作一定是所有操作的一个后缀和 这样的话我们只要对于每
阅读全文
摘要:题面 "传送门" 题解 ~~我对线代一无所知~~ ~~如果下面有啥说错的地方请说出来省的我一辈子都搞不明白~~ ~~如果你没看懂以下在讲什么不要紧,因为我也没看懂~~ 首先,关于$A\times B \equiv C \pmod{2}$的方程的一组合法解,$C$的列向量必定在$A$的列向量的线性空间
阅读全文
摘要:题面 "传送门" 题解 ~~我的线代学得跟屎一样看题解跟看天书一样所以不要指望这题我会写题解~~ "这里"
阅读全文
摘要:题面 "传送门" 题解 我们设$A=\begin{bmatrix}1 & 1 \\ 1 & 0\end{bmatrix}$,那么$A^n$的左上角就是$F$的第$n$项 所以我们现在转化为求 $$\sum_{i=0}^n[k|i]{n\choose i}A^i$$ 把$[k|i]$单位根反演一下 $
阅读全文
摘要:题面 "传送门" 前置芝士 $BSGS$ 什么?你不会$BSGS$?百度啊 原根 对于素数$p$和自然数$a$,如果满足$a^x\equiv 1\pmod{p}$的最小的$x$为$p 1$,那么$a$就是$p$的一个原根 离散对数 对于素数$p$,以及$p$的一个原根$g$,定义$y$为$x$的离散
阅读全文
摘要:题面 茉优最近研究发现,一个人的想愿能力可以认为是字符串S的一个子串S[l,r],而连接值可以认为是这个子串的本质不同子序列个数。现在她想验证她的结论是否正确,于是她给了你Q个询问,希望你帮她来计算,注意空串也是子序列。 题解 ~~考场上暴力都打错~~ 先考虑暴力,设$f_i$为$i$下标为终止位置
阅读全文
摘要:"传送门" uoj上的数据太毒了……也可能是我人傻常数大的缘故…… 三种血量的奴隶主加起来不超过$8$个,可以枚举每种血量的奴隶主个数,那么总的状态数只有$165$种,设$dp_{t,i,j,k}$表示$t$时刻的时候$i$个一血奴隶主,$j$个二血奴隶主,$k$个三血奴隶主的概率,那么转移很明显
阅读全文
摘要:"传送门" "题解" 抄代码$20$分钟,搞懂题解在干嘛仨小时→_→ 到今天才算真正搞明白$FWT$在干吗了 本题 首先转移关系都是恒定的,设它为一个矩阵$B$,那么要求的就是$f_n=f_0B^n$ 定义三进制不退位减法$\ominus$,三进制不退位加法$\oplus$,这两个互为逆运算(可以类
阅读全文
摘要: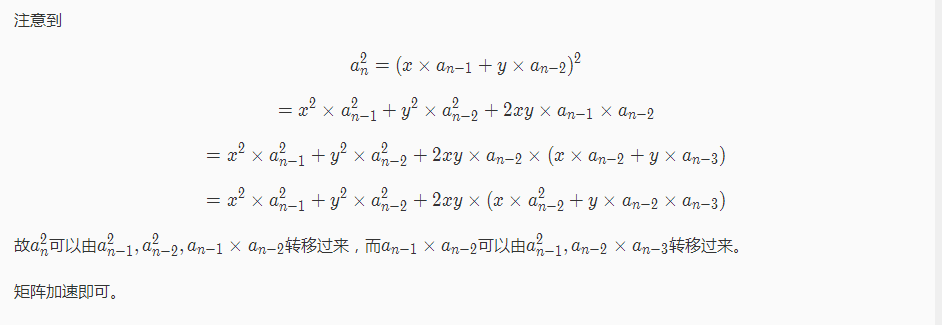 ``` //minamoto #include #define R register #define ll long long #define fp(i,a,b) for(R int i=a,I=b+1;iI;-...
阅读全文
摘要:"传送门" 数列的特征方程和特征根老师上课好像讲过然而我没听……以后老师上数学课要认真听了QAQ 设$x=\frac{1+\sqrt{5}}{2},y=\frac{1 \sqrt{5}}{2}$,那么$x,y$是$t^2=t+1$的两个解,也就是数列$F_n=F_{n 1}+F_{n 2}$的特征根
阅读全文
摘要:"传送门" 我现在还是不明白为什么NOIPd2t3会是一道动态dp…… 首先关于动态dp可以看 "这里" 然后这里就是把把矩阵给改一改,改成这个形式$$\left[dp_{i 1,0},dp_{i 1,1}\right]\times \left[\begin{matrix}\infty&ldp_{i
阅读全文
摘要:"传送门" "shadowice巨巨" 太强啦 表示连树剖都不会直接来肝这个近乎LCT的很懵逼啊……于是一个晚上就过去了…… 首先,这题本质上就是个没有上司的舞会,然而带修改 先考虑正常的dp方程,设$dp_{u,0}$表示该点不选的最大收益,$dp_{u,1}$表示该点选的最大收益,则有$$dp_
阅读全文
摘要:"传送门" 为啥我就没看出来有循环节呢…… 打表可得,这个数列是有循环节的,循环节为$10^9+6$,然后分块预处理,即取$k=sqrt(10^9+6)$,然后分别预处理出转移矩阵$A$的$A^1,A^2,...,A^{k 1}$和$A^k,A^{2k},...$,那么每一次就能$O(1)$回答询问
阅读全文
摘要:"传送门" 话说邻接矩阵居然还能快速幂的么…… 把原图的邻接矩阵$G$打出来,那么$G[u][v]$表示一秒后$u$到$v$的方案数,$G^2[u][v]$表示$2$秒后的方案数……于是只要矩阵快速幂计算$G^k$即可 然而有食人鱼,会导致某些点在某些时刻不能走。发现$lcm(2,3,4)=12$,
阅读全文
摘要:"传送门" 官方题解 话说最后的答案忘记取模了结果连暴力都挂了可海星……
阅读全文
摘要:"传送门" 首先不难设$f[i][j]$表示跳到$(i,j)$的方案数,那么不难得到如下转移 $$f[i][j]=\sum\limits_{k=1}^{\frac n2}f[i 2k+1][j 1]+f[i 2k+1][j]+f[i 2k+1][j+1]$$ 然后维护两个前缀和$s1,s2$,分别表
阅读全文
摘要:"传送门" 题目大意:问从起点走到终点,不能立刻走上一条走过的边,长度为$t$的方案数 按点考虑会很麻烦,我们考虑按边来考虑。先把无向边给拆成两条有向边,记$dp[i][j]$表示在$i$时刻走过第$j$条边到了$j$边的终点的方案数。那么它可以从$j$边的终点继续走,只要走的下一条边不是$j$的反
阅读全文
摘要:"传送门" 线性代数真的好珂怕……以下如果有漏洞欢迎指出 定义矩阵的三种初等行变换: 1.交换某两行 2.将某一行的所有元素乘上$k$($k\neq 0$) 3.将某一行的所有元素乘上$k$加到另一行去 每一个初等变换都对应一个初等矩阵,即矩阵$A$做某一线性变换等价于用一个对应的初等矩阵左乘$A$
阅读全文
摘要:传送门 大佬讲的真吼->这里 首先考虑dp,设$f[i][j]$表示长串匹配到第$i$位,短串最多匹配到$j$位时的方案数 那么答案就是$\sum_{i=0}^{m-1}f[n][i]$ 然后考虑一下dp的转移,一种是加进的新字符$i+1$与$j+1$匹配,那么$dp[i][j]$可以直接转移到$d
阅读全文


 浙公网安备 33010602011771号
浙公网安备 33010602011771号