状态压缩——炮兵阵地

（第一次做状压，难死我了QAQ）

题目描述

司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

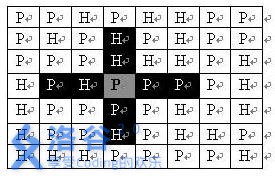
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入输出格式

输入格式：

 

第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符（‘P’或者‘H’），中间没有空格。按顺序表示地图中每一行的数据。N≤100；M≤10。

 

输出格式：

 

仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

 

输入输出样例

输入样例#1： 复制

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

输出样例#1： 复制

这道题在我没有学过状压dp之前，似乎只有搜索这一条路可以走，这么大的规模（搜索肯定是不可能的了）

那么状态压缩动态规划就出现了，状态压缩动态规划又称为集合动态规划。

顾名思义，这种动态规划是将集合信息为状态记录的特殊动态规划，主要有传统的集合动态规划和基于连通性状态压缩的动态规划。

一般的动态规划根据整体，从中提取中几个关键信息，同时，划分阶段将问题具备无后效性和最优子结构性质，然后根据已知的信息对于各个阶段进行决策，

但是对于状态压缩动态规划而言，一般的简单状态描述已经无法满足无后效性原则了，所以我们需要对于多个元素的状态进行压缩，这便是状态压缩动态规划的由来

（一看就知道不是我说的o(*￣︶￣*)o）

这道题呢？

发现一个炮兵的防止最多影响到下面的两层，所以我们对于此题的动态规划

用状态f[i][j][k]表示当前放到了哪一层，这层的状态为k，上层的状态是j（j,k均想象为2进制数，对于二进制上第i-1位的1表示在第i个位置上有没有放炮兵，我们用十进制存储）

那么转移就为

  f[i][j][k]:=max(f[i-1][w][j])+g[k]（g[k]表示k中的炮兵数量）(w枚举合法状态同时判断这三行的放置是否合法)

那么我们怎么枚举生成状态呢

 for i:=0 to (1<<m)-1 do
  if ((i and (i<<1)=0) and (i and (i<<2)=0)) then
  begin
    inc(num);//状态数加+1
    sta[num]:=i;
    g[num]:=bits(i);//计算i中1的数量
    if (i and map[1]=0) then f[1][0][num]:=g[num];//手动dp第一层，判断和第一层的地形是否合法
  end;

然后，我们需要对于当前层的状态枚举上两层的状态来判断是否是合法的

 for i:=3 to n do//我好想莫名其妙的初始化了第2层
    for j:=1 to num do//枚举所以状态
     if sta[j] and map[i]=0 then//和第i层的地形是否合法
     for k:=1 to num do//枚举上一层的状态
     if sta[k] and sta[j]=0 then//上一层和这一层是否合法
      for l:=1 to num do//枚举上上层状态
       if ((sta[l] and sta[k]=0) and (sta[l] and sta[j]=0)) then//上上层和上层和当前层是否有冲突
        f[i][k][j]:=max(f[i][k][j],f[i-1][l][k]+g[j]);//转移

　　所以，代码如下

 var
   n,m,i,j,k,num,l,ans:longint;
   map,g,sta:array[0..10000] of longint;
   f:array[0..100,0..100,0..100] of longint;
   x:char;
function max(a,b:longint):longint;
begin
  if a>b then exit(a)
  else exit(b);
end;
function bits(d:longint):longint;
var sum:longint;
begin
  sum:=0;
  while (d>0) do
  begin
    inc(sum);
    d:=d-((d) and (-d));
  end;
  exit(sum);
end;
begin
  readln(n,m);
  for i:=1 to n do
  begin
    for j:=0 to m-1 do
    begin
      read(x);
      if (x='H') then map[i]:=map[i]+(1<<j);
    end;
    readln;
  end;
  for i:=0 to (1<<m)-1 do
  if ((i and (i<<1)=0) and (i and (i<<2)=0)) then
  begin
    inc(num);
    sta[num]:=i;
    g[num]:=bits(i);
    if (i and map[1]=0) then f[1][0][num]:=g[num];
  end;
  for i:=1 to num do
    for j:=1 to num do
    if ((sta[i] and sta[j]=0) and (map[2] and sta[j]=0)) then
    f[2][i][j]:=max(f[2][i][j],f[1][0][i]+g[j]);
  for i:=3 to n do
    for j:=1 to num do
     if sta[j] and map[i]=0 then
     for k:=1 to num do
     if sta[k] and sta[j]=0 then
      for l:=1 to num do
       if ((sta[l] and sta[k]=0) and (sta[l] and sta[j]=0)) then
        f[i][k][j]:=max(f[i][k][j],f[i-1][l][k]+g[j]);
  for i:=1 to num do
    for j:=1 to num do
    ans:=max(ans,f[n][i][j]);
  writeln(ans);
end.

　其实，这类方法我们需要跟加精确的计算时间复杂度

  看上去枚举三层的状态需要8^n，但是我们发现一行上合法的状态都不会超过60个，那么8^n次直接就变成了60^3,emmm然后就过了

  其实我们枚举了很多不必要的状态，因为发现向上层枚举我们很难优化，那不如就向下枚举，向下枚举我们就会发现下面的放置一定是上面0状态的子集，

  那么时间复杂度就会接近我们程序的时间复杂度（似乎状压dp的时间复杂度比较玄学）

  那么这道题就讲到这里了