长链剖分

part1：具体实现

流程可以看 这里

---

part2：时间/空间 复杂度分析：

1. 时间复杂度：考虑一个点什么时候会对 dp 产生贡献，以一条链为单位，这一条链对 dp 有贡献，只有在这条链作为轻链“接入”另一条链的时候，而它作为轻链只有一种情况。所以一条链只会被计算 \(1\) 次，所有的链恰好可以覆盖完整棵树。所以总时间复杂度为 \(O(n)\)
2. 空间复杂度：其实能节省空间的原理还是：在遍历完结点 \(son[u]\) 之后，\(dp_{son[u],i}\) 就不再有用，我们就把这些空间分配给它的父亲 \(u\)。

part3：重儿子的分析

为什么要用深度最大的点作为它的重儿子，好像随便取重儿子复杂度也没有问题?

事实上正确性可能有问题。

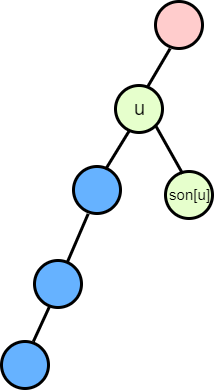
比如上图，如果我们把重儿子随便设，然后更新到 \(u\) 都是没有问题的，但是如果 \(u\) 作为 \(fa_u\) 的轻儿子，要用 \(u\) 更新 \(fa_u\)，这个时候应该遍历 \(u\) 的多少深度呢？如果按照最深的来更新，那么蓝色的那一条链就不止被用了一次，如果按照绿色的链长来更新，就没有遍历完 \(u\) 最深的深度，答案可能就是错的。

part4：两个应用

应用1：在 \(O(n\log n)\) 的预处理后，\(O(1)\) 求任意一点的 \(k\) 级祖先。这里

应用2：优化以深度为下标的树形DP。这个就很多了，上面的那道题就是这个应用。