机器学习数学基础-2-微积分

微积分

微分知识点

1. \(\Delta x=dx\)
2. \(\Delta y\) 是 \(dx\) 的曲线增量
3. \(dy\) 是 \(dx\) 的切线增量
4. \(\Delta y=dy+o(\Delta x)\)

---

定积分

当 \(\lVert\Delta x\rVert\to 0\)时，总和 \(S\) 总是趋于确定的极限 \(I\)，则称极限 \(I\) 为函数 \(f(x)\) 在曲线 \([a,b]\) 上的定积分

\[\int_{a}^{b}f(x)dx=I=\lim_{\lambda\to 0}\sum_{i=1}^{n}f(\xi_i)\Delta x_i \]

• \(a,b\) 分别称为积分上限和积分下限
• \(f(x)\) 称为被积函数
• \(dx\) 称为积分变量
• \(f(x)dx\) 整体称为被积表达式

积分值和被积函数与积分曲线有关，与积分变量字母无关，即

\[\int_a^bf(x)dx=\int_a^bf(t)dt=\int_a^bf(u)du \]

当函数 \(f(x)\) 在区间 \([a,b]\) 上的定积分存在的时候，称 \(f(x)\) 在区间 \([a,b]\) 上可积

---

定积分的性质

• \(\int_a^b[f(x)\pm g(x)]dx=\int_a^bf(x)dx\pm \int_a^bg(x)dx\)
• \(\int_a^bkf(x)dx=k\int_a^bf(x)dx\)，其中 \(k\) 为常数
• 若 \(a<c<b\)，则 \(\int_a^bf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx\)
• 若在区间 \([a,b]\) 上 \(f(x)\ge0\)，则 \(\int_a^bf(x)dx\ge 0\)，其中 \(a<b\)

第一中值定理

如果函数 \(f(x)\) 在闭区间 \([a,b]\) 上连续，则在积分区间 \([a,b]\) 上至少存在一点 \(\xi\)，使得 \(\int_a^bf(x)dx=f(\xi)(b-a),\ (a\le\xi\le b)\)

---

积分上限函数

函数 \(f(x)\) 在区间 \([a,b]\) 上连续，对于定积分 \(\int_a^xf(x)dx\) 每一个取值的 \(x\) 都有一个对应的定积分值，记作 \(\Phi(x)=\int_a^xf(t)dt\)

如果 \(f(x)\) 在区间 \([a,b]\) 上连续，则积分上限函数就是 \(f(x)\) 在 \([a,b]\) 上的原函数

---

牛顿-莱布尼茨公式

如果 \(F(x)\) 是连续函数 \(f(x)\) 在区间 \([a,b]\) 上的一个原函数，则：

\[\int_a^bf(x)dx=F(b)-F(a) \]

几何解释：

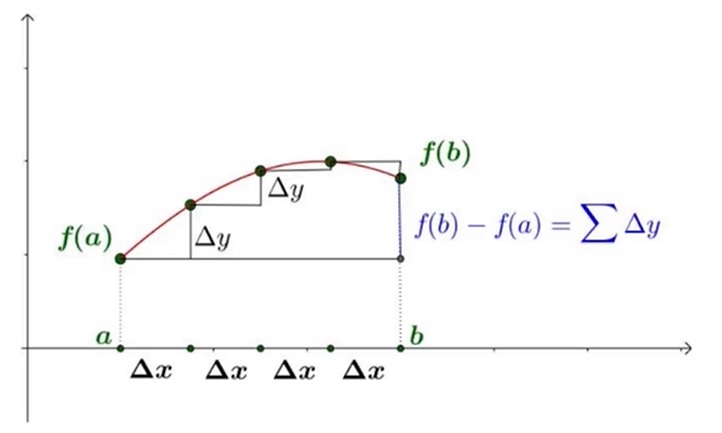
\(f(b)-f(a)=\sum dy\)，由于 \(dy=f^{'}(x)dx\)，那么 \(f(b)-f(a)=\sum f^{'}(x)dx=\int_a^bf^{'}(x)dx\)

---

微积分基本公式

有 \(f(x)\in C[a,b]\)，且 \(F^{'}(x)=f(x)\)

\[\underbrace{\int_a^bf(x)dx=f(\xi)(b-a)}_{\text{积分中值定理}}=\underbrace{F^{'}(\xi)(b-a)=F(b)-F(a)}_{\text{微分中值定理}} \]