9.29 联赛组作业

E. Train Car Selection

---

Solution

首先对于1、2操作加入的\(k\)个数，只有第一个数对答案有贡献。
然后用一个单调栈（栈中A从大到小）维护答案。

首先设\(k[i]\)表示i在原队列中的位置。
十分显然：对于 \(k[i] < k[j]\)且\(a[i] < a[j]\) ，那么 \(a[j]\) 无论何时都不可能比 \(a[i]\) 小。

设对于栈中相邻元素 \(i, j(a[i] > a[j])\) 的“增长率”为\(\frac{a[i] - a[j]}{k[i] - k[j]}\)，
其大小表示变化为 \(a[i] < a[j]\) 的快慢程度（相对其他元素对变化所需经过的轮数）

对于栈中元素 \(i,j,k(a[i] > a[j] > a[k])\) ，如果 \(\frac{a[i] - a[j]}{k[i] - k[j]} < \frac{a[j] - a[k]}{k[j] - k[k]}\) ，
那么元素 \(j\) 始终无法成为最小值，可以直接弹出栈。

然后对于一次修改，可以存下栈中元素 \(i\) 上一次的修改值 \(B, S\)，如果需要对 \(i\) 进行修改 \(b, s\) 的话，就可以十分简单地修改了。

知道了这些就很好做啦。

 

G. Privatization of Roads in Treeland

---

Solution

将每个点按度数从大到小排序，排序后前k个点作为“坏点”，最小的颜色数就是第 \(k + 1\) 个点的度数，方案随意输出即可。
证明：暂时略

 

F2. Same Sum Blocks (Hard)

---

Solution

\(n \leq 1500\)，这不是暗示我们可以 \(n^2\) 吗！

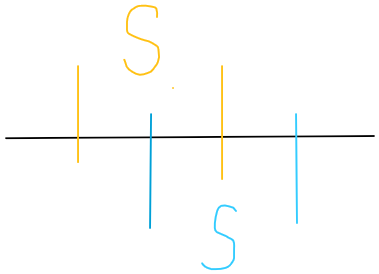
首先对于两段和同为 \(S\)，重合的区间，可以发现，如果我们要最大和为 \(S\) 的区间的个数，后面的那个区间（蓝色区间）是没用贡献的（或者说可以不算的）。
其次，最多只有 \(n^2\) 种不同的区间和。

那么，可以用一个权值线段树来维护每一种权值和的区间数，以及最后一个区间的右端点。
考虑枚举区间右端点 \(j\)，然后枚举左端点 \(i\)，
如果区间 \([i, j]\) 同上一个和相同区间不相交（线段树判断），那么更新线段树内的值，
如果相交，那就不要 \([i, j]\)了。

 

F. Destroy it!

---

Solution

设 \(f_{i,j}\) 表示第 \(i\) 块， 前面已有 \(j\) 个数 \((0 \leq j \leq 9)\) 的最大权值和。
对于每一块来说，至多花费3，所以只有7种转移方式：

1. 1
2. 2
3. 3
4. 1 + 1
5. 1 + 2
6. 1 + 1 + 1
7. 一个都不选

（这里数字代表花费为cost的最大价值卡牌）
7种可以预处理出来，转移显然。
注意转移方式4567可能会跨越“10”。

 

F. Scalar Queries

---

Solution

考虑如何计算以 \(i\) 为右端点所有区间的和 \(f(i)\)，可以发现 \(f(i)\) 其实等于 \(f(i - 1)\)（以 \(i-1\) 为右端点的区间的和） 加上加入 \(i\) 后的贡献。

贡献分两类计算：
第一类是 \(i\) 的贡献。
首先可以发现，以 \(i\) 为右端点，\(a[i]\) 的系数是这样子的：

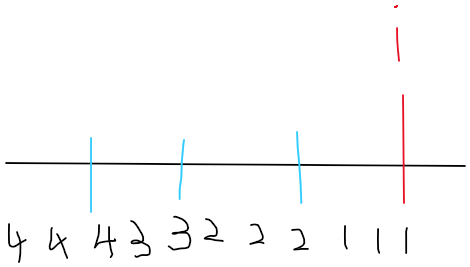
（蓝线代表 \(a\) 小于 \(a[i]\) 的数）

那么十分显然的是，设 \(x_i\) 表示 \(a[x_i] < a[i]\)，那么 \(a[i]\) 的系数和就等于 \(\sum{x_i}\)。
所以第一类的贡献就为 \(a[i] * \sum{x_i}\)

第二类贡献是 \(i\) 加入后区间中 \(a > a[i]\) 的数所需要加的贡献。
十分显然就等于 \(\sum{a[j] * j} (a[j] > a[i])\)

然后答案就很好计算了，权值线段树维护即可。
这题不太确定希望没锅

 

E. Range Deleting

---

Solution

设 \(g(l,r) = 0 / 1\) 表示删去 \(a_i(l \leq a_i \leq r)\) 后序列是否不下降。
考虑固定左端点 \(l\)，可以发现 \(g(l, r)\) 具有单调性，证明：设 \(r (l \leq r \leq x)\) 为最小的 \(r\) 使得 \(g(l, r) = 1\)，那么显然 \(g(i, j) = 0 (i \leq j < r)\) 且 \(g(i, j) = 1 (r \leq j \leq x)\)。
那么就可以枚举左端点 \(i\)，二分出最小的右端点 \(j\) 使得 \(g(i, j) = 1\)，以 \(i\) 为左端点对答案的贡献就是 \(x - j + 1\)。

再考虑 \(g(l, r)\) 怎么求，可以发现 \(g(l, r)\) 可以分成三个部分：
1.\(a_i (1 \leq a_i < l)\) 是否不下降
2.\(a_i (r < a_i \leq x)\) 是否不下降
3.\(max(i) (1 \leq a_i < l)\) 是否小于 \(min(j) (r < a_j \leq x)\)

复杂度 \(O(nlogn)\)