Codeforces Round #735 (Div. 2)

打铁局，div2掉分了，乐

补题去了

目录：

• A. Cherry

• B. Cobb

• C. Mikasa

• D. Diane

• E. You

 

A. Cherry

time limit per test ： 1 second

memory limit per test ： 256 megabytes

You are given nn integers a1,a2,…,an. Find the maximum value of max(al,al+1,…,ar)⋅min(al,al+1,…,ar) over all pairs (l,r) of integers for which 1≤l<r≤n.

Input

The first line contains a single integer t (1≤t≤10000)  — the number of test cases.

The first line of each test case contains a single integer n (2≤n≤10^5).

The second line of each test case contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤10^6).

It is guaranteed that the sum of nn over all test cases doesn't exceed 3⋅10^5.

Output

For each test case, print a single integer  — the maximum possible value of the product from the statement.

Example

input

4
3
2 4 3
4
3 2 3 1
2
69 69
6
719313 273225 402638 473783 804745 323328

output

12
6
4761
381274500335

Note

Let f(l,r)=max(al,al+1,…,ar)⋅min(al,al+1,…,ar)f(l,r)=max(al,al+1,…,ar)⋅min(al,al+1,…,ar).

In the first test case,

• f(1,2)=max(a1,a2)⋅min(a1,a2)=max(2,4)⋅min(2,4)=4⋅2=8f(1,2)=max(a1,a2)⋅min(a1,a2)=max(2,4)⋅min(2,4)=4⋅2=8.
• f(1,3)=max(a1,a2,a3)⋅min(a1,a2,a3)=max(2,4,3)⋅min(2,4,3)=4⋅2=8f(1,3)=max(a1,a2,a3)⋅min(a1,a2,a3)=max(2,4,3)⋅min(2,4,3)=4⋅2=8.
• f(2,3)=max(a2,a3)⋅min(a2,a3)=max(4,3)⋅min(4,3)=4⋅3=12f(2,3)=max(a2,a3)⋅min(a2,a3)=max(4,3)⋅min(4,3)=4⋅3=12.

So the maximum is f(2,3)=12f(2,3)=12.

In the second test case, the maximum is f(1,2)=f(1,3)=f(2,3)=6f(1,2)=f(1,3)=f(2,3)=6.

——————————————————————————

题意：

给定长度为n的序列，考虑所有的l，r满足1≤l<r≤n：在区间a[l]~a[r]中，计算h=max(a[l]~a[r])*min(a[l]~a[r])。在所有的l和r组合中，找到h的最大值。

思路：

最开始考虑用划窗去维护最大最小值，由贪心思想应该让max和min尽可能的大，即max为最大的数，min为次大的数。后来分析发现，对于a[ ]={ 1, 4, 6, 3, 2, 8 }这样的一组，无法做到max=8，min=6的情况。因为6和8之间还有3,2来阻止min变大。所以对于所有的l,r，仅取r=l+1时为最优解，即取两个相邻的数。在两个相邻的数中，可以保证max和min不被其他更大或更小的数干扰。

实现：

找相邻的数乘积真的是签中签了，for一遍的事情。考虑到数据规模1≤ai≤10^6，记得开long long！

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int t,n;
    long long maxx,tmp,a[100005];
    cin>>t;
    while(t--)
    {
        maxx=0;
        cin>>n;
        for(int i=0;i<n;i++)
            cin>>a[i];
        for(int i=0;i<n-1;i++)
        {
            tmp=a[i]*a[i+1];
            if(tmp>maxx)
                maxx=tmp;
        }
        cout<<maxx<<endl;
    }
    return 0;
}

 

 

 

 

B. Cobb

time limit per test ： 1 second

memory limit per test ： 256 megabytes

You are given n integers a1,a2,…,an and an integer k. Find the maximum value of i⋅j−k⋅(ai|aj)over all pairs (i,j) of integers with 1≤i<j≤n. Here, | is the bitwise OR operator.

Input

The first line contains a single integer tt (1≤t≤10000)  — the number of test cases.

The first line of each test case contains two integers nn (2≤n≤10^5) and kk (1≤k≤min(n,100)).

The second line of each test case contains nn integers a1,a2,…,an (0≤ai≤n).

It is guaranteed that the sum of nn over all test cases doesn't exceed 3⋅10^5.

Output

For each test case, print a single integer  — the maximum possible value of i⋅j−k⋅(ai|aj).

Example

input

4
3 3
1 1 3
2 2
1 2
4 3
0 1 2 3
6 6
3 2 0 0 5 6

output

-1
-4
3
12

Note

Let f(i,j)=i⋅j−k⋅(ai|aj).

In the first test case,

• f(1,2)=1⋅2−k⋅(a1|a2)=2−3⋅(1|1)=−1f(1,2)=1⋅2−k⋅(a1|a2)=2−3⋅(1|1)=−1.
• f(1,3)=1⋅3−k⋅(a1|a3)=3−3⋅(1|3)=−6f(1,3)=1⋅3−k⋅(a1|a3)=3−3⋅(1|3)=−6.
• f(2,3)=2⋅3−k⋅(a2|a3)=6−3⋅(1|3)=−3f(2,3)=2⋅3−k⋅(a2|a3)=6−3⋅(1|3)=−3.

So the maximum is f(1,2)=−1.

In the fourth test case, the maximum is f(3,4)=12.

 

 

 

 

C. Mikasa
time limit per test ：1 second
memory limit per test ：256 megabytes
You are given two integers n and m. Find the MEX of the sequence n⊕0,n⊕1,…,n⊕m. Here, ⊕ is the bitwise XOR operator.

MEX of the sequence of non-negative integers is the smallest non-negative integer that doesn't appear in this sequence. For example, MEX(0,1,2,4)=3, and MEX(1,2021)=0.

Input
The first line contains a single integer t (1≤t≤30000) — the number of test cases.

The first and only line of each test case contains two integers n and m (0≤n,m≤109).

Output
For each test case, print a single integer — the answer to the problem.

Example
input

5
3 5
4 6
3 2
69 696
123456 654321

output

4
3
0
640
530866

Note
In the first test case, the sequence is 3⊕0,3⊕1,3⊕2,3⊕3,3⊕4,3⊕5, or 3,2,1,0,7,6. The smallest non-negative integer which isn't present in the sequence i. e. the MEX of the sequence is 4.

In the second test case, the sequence is 4⊕0,4⊕1,4⊕2,4⊕3,4⊕4,4⊕5,4⊕6, or 4,5,6,7,0,1,2. The smallest non-negative integer which isn't present in the sequence i. e. the MEX of the sequence is 3.

In the third test case, the sequence is 3⊕0,3⊕1,3⊕2, or 3,2,1. The smallest non-negative integer which isn't present in the sequence i. e. the MEX of the sequence is 0.

 

 

 

 

D. Diane

time limit per test  :  1 second

memory limit per test  :  256 megabytes

You are given an integer n. Find any string s of length n consisting only of English lowercase letters such that each non-empty substring of s occurs in ss an odd number of times. If there are multiple such strings, output any. It can be shown that such string always exists under the given constraints.

A string a is a substring of a string b if a can be obtained from bb by deletion of several (possibly, zero or all) characters from the beginning and several (possibly, zero or all) characters from the end.

Input

The first line contains a single integer t (1≤t≤500) — the number of test cases.

The first line of each test case contains a single integer nn (1≤n≤105).

It is guaranteed that the sum of nn over all test cases doesn't exceed 3⋅10^5.

Output

For each test case, print a single line containing the string ss. If there are multiple such strings, output any. It can be shown that such string always exists under the given constraints.

Example

input

4
3
5
9
19

output

abc
diane
bbcaabbba
youarethecutestuwuu

Note

In the first test case, each substring of "abc" occurs exactly once.

In the third test case, each substring of "bbcaabbba" occurs an odd number of times. In particular, "b" occurs 55 times, "a" and "bb" occur 3 times each, and each of the remaining substrings occurs exactly once.

 

题意：

给定序列s的长度n，构造一个可能的序列满足：s的任何子列在s中出现的次数为奇数次。

思路：

①举例：

对于长度为9的序列aaaaaaaaa，子序列a出现了9次，aa出现了8次，aaa出现了7次......aaaaaaaaa出现了9次。

而对于长度为8的序列aaaaaaaa，子序列a出现了8次，aa出现了7次，aaa出现了6次......aaaaaaaa出现了8次。

②观察：

由上两个例子，可得如下表格

 

 所以，按照子序列的奇偶性去看表格时，当子序列是奇/偶时，为使其次数认为奇数次，可以选择奇+偶来构造

③构造：

构造时，需要两串x来满足上面的推论，一串x为奇数个，另一串为偶数个。这样x的总个数是（2*k）+(2*k+1)个。

此时x的任意长度子串必满足出现次数为奇数，前后两串x满足->（前奇后偶，前偶后奇）

若n为偶数，则需要用1个x以外的字符将两串x分隔开（例如y）。

若n为奇数，则需要2个x以外的字符将两串x分隔开。同时，若选择了2个一样的字符，则又会出现不满足奇数个的情况。故只能选用两个不同的，非x的字符（例如y,z）

④一些细节：

由于上文构造时默认总长度n很大，但是不能遗漏了比如n==1的情况，n==1时只要1个任意字符串就可以。不加特判会按照奇数个的情况起码打印两个非x字符！

最后，上代码：

D-

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int t,n;
    cin>>t;
    while(t--)
    {
        cin>>n;
        if(n==1)
            cout<<"x"<<endl;
        else
        {
            for(int i=1;i<n/2;i++)
                cout<<"x";
            cout<<"y";
            if(n%2)
                cout<<"z";
            for(int i=0;i<n/2;i++)
                cout<<"x";
            cout<<endl; 
        }        
    }
    return 0;
}

 

 

 

E. You

time limit per test ： 5 seconds

memory limit per test ： 256 megabytes

You are given a tree with nn nodes. As a reminder, a tree is a connected undirected graph without cycles.

Let a1,a2,…,an be a sequence of integers. Perform the following operation exactly n times:

• Select an unerased node uu. Assign au:= number of unerased nodes adjacent to u. Then, erase the node u along with all edges that have it as an endpoint.

For each integer k from 1 to n, find the number, modulo 998244353 , of different sequences a1,a2,…,an that satisfy the following conditions:

• it is possible to obtain aa by performing the aforementioned operations exactly nn times in some order.
• gcd(a1,a2,…,an)=kgcd⁡(a1,a2,…,an)=k. Here, gcdgcd means the greatest common divisor of the elements in a.

Input

The first line contains a single integer tt (1≤t≤10000)  — the number of test cases.

The first line of each test case contains a single integer n (2≤n≤10^5).

Each of the next n−1 lines contains two integers uu and vv (1≤u,v≤n) indicating there is an edge between vertices u and v. It is guaranteed that the given edges form a tree.

It is guaranteed that the sum of n over all test cases doesn't exceed 3⋅10^5.

Output

For each test case, print nn integers in a single line, where for each k from 1 to n, the k-th integer denotes the answer when gcdgcd equals to k.

Example

input

2
3
2 1
1 3
2
1 2

output

3 1 0
2 0

Note

In the first test case,

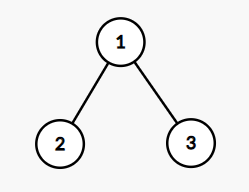
• If we delete the nodes in order 1→2→31→2→3 or 1→3→21→3→2, then the obtained sequence will be a=[2,0,0]a=[2,0,0] which has gcdgcd equals to 22.
• If we delete the nodes in order 2→1→32→1→3, then the obtained sequence will be a=[1,1,0]a=[1,1,0] which has gcdgcd equals to 11.
• If we delete the nodes in order 3→1→23→1→2, then the obtained sequence will be a=[1,0,1]a=[1,0,1] which has gcdgcd equals to 11.
• If we delete the nodes in order 2→3→12→3→1 or 3→2→13→2→1, then the obtained sequence will be a=[0,1,1]a=[0,1,1] which has gcdgcd equals to 11.

Note that here we are counting the number of different sequences, not the number of different orders of deleting nodes.