lxl 又来讲课的记录（没写完）

题目略加删减。

Day1

模拟费用流。

单向链的结构是非常普通的模拟费用流形式。

费用流有几个性质：凸的；增广路不会经过同一个点。

P4694

单向链的模板。维护方法是线段树对信息和反向链次数序列 \(h\) 维护，维护其最小值下的前缀后缀等等。

好多和这个同质的题目，没有什么本质性的更新？？

百度之星2024决赛T11

快速维护增广路，由于不会重复经过一个点的特性，一个增广路相当于若干次一个集合和另外集合的替换。建出完全图，可以变成一个路径。使用堆维护两点边权，最后 Floyed 之类的可以了。

P9168

还没写

U548997

要最大化曼哈顿距离。

一个性质：若把线段两端点分别横纵做直线划分为九个区域，则区域内的点各自和线段端点曼哈顿距离之和可以拆开；并且正确的范围是九个线性式子中最大的。

好，现在可以容易用九个中转点建图。类似于前面百度之星那个堆维护边权再最短路即可。

Day2

P11369

依然是 DAG 可达性。根号重构之后把修改查询的点拉出来暴力看看不经过修改边被哪些点到达，好消息是这几乎总是 \(O(nm/w)\) 的。每次查询就把修改边加上，对这些关键点跑 BFS 即可。这里实际上块长可以搞很小。

QOJ1851

根号重构。找到每个点最后一次被影响的二操作是容易的。对于三操作扫描值域，可以被更新的一定是一段“前缀”，BFS 去更新即可。

P5428

找出 \(n\) 条线段的较少的全部交点。

无交点/只在端点相交线段的特性是横着扫描的话相对顺序不改变。现在有交点，插入的时候看看相邻的变换顺序会在 \(x=\) 多少的时候发生即可。

P5073

首先第一件事是最大子段和信息是可以由 pre suf ans sum 合并来的，现在考虑在线段树上获取其信息即可。

考察 pre，随着 x 的上升更长的后缀会更有效，最终一个凸包的点会被保留。suf 和 ans 是类似的。

如果线段树预处理凸包，获得 \(O(n\log n)\) 的预处理时间空间，离线扫描可以使得询问均摊 \(O(n\log n)\)。

比较神秘的一点是按照 \(n/\log n\) 大小分块获得 \(O(n)\) 空间和时间复杂度不变。

P11235

题面太长了。

核心问题是根据最值分治考虑发现封闭序列是无交或包含的。然后向上合并答案：每个封闭区间保留 \(x\) 个的答案 \(y\) 应该是凸的，前面忘了中间忘了直接合并即可。

P4062

直接枚举绝对众数，序列转成 \(\pm 1\)。注意到可能被覆盖的 \(-1\) 数量 \(~cnt_1\)。从右到左（任意顺序？）把每个 \(1\) 往右的第一个未匹配 \(-1\) 和它匹配，向左同理。未被覆盖的 \(-1\) 是不可能被合法区间覆盖的，这样做到了线性。

如果希望非常线性即不使用一般并查集处理匹配的话有压位并查集。

P7882

使用莫队和上面的方法得到 \(O(cnt\sqrt q+q)\) 的复杂度是比较优秀的，因此根号分治大的跑莫队。

小的就暴力把这些区间拉出来跑二维数点，总区间数是 \(O(n\sqrt n)\) 的。

Day3

QOJ8229

换维扫描线，转为括号匹配考虑。其实括号本质上没什么优越，但是括号知道单侧递归的经典问题，然后直接套用。

QOJ8672

有个东西叫插入标记回收，就是说查询 \(f_l\circ f_{l+1}\circ \dots\circ f_{r}(x)\)，换维扫描线扫描序列，在 \(l\) 的时候插入 \(x\)，每次全局复合，在 \(r\) 时候删除这个东西或者根本不管即可。

然后直接完成。

P11622

没什么大区别，但是据说平衡树是可以有交合并的，证明方法是取 \(\sum \log \Delta\) 作为势能分析，然后合并 \(x,y\) 方法是取优先级高的 \(x\) 然后把 \(y\) 按 \(val(x)\) 劈成三段，左右分别合并，中间删掉并到 \(x\) 上（否则复杂度大概是假的）。

芝麻糊题目

还没写

Day4

P8337

精细处理可以把每个 \(r,k\) 对于线性基/颜色数为 \(2^k\) 的左端点区间处理出来。原理上询问应该需要 \(\log^2\)，但是注意到这个左端点区间对于每个 \(k\) 关于 \(r\) 为单调（左右端点都单调）因此容易解决。

P9057

换维扫描线，前面忘了后面忘了总之可能维护。

T365455

有若干区间，若干次问能否恰好覆完一个区间。

对 \(r\) 扫描线，维护每个点想被某区间覆盖最大的左端点，是区间取 max 区间问 min 形式。

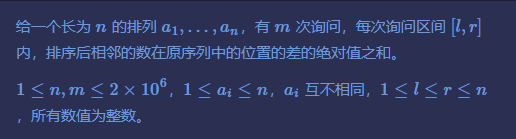
P11695

上题动态插入查询的版本。

扫描线的按顺序限制是麻烦的，因此线段树分治陷入万般困局，然后直接 KDT 之类确实前途不明。

对序列分治（，，，），据信降低了区间的两维的限制。考虑跨过区间的（显然一个区间不能用多次）和未跨过区间的。

考察跨过区间的，最终得到的结果应该是左右各能最终蔓延到哪里；具体方法是扫描左侧逐步加入区间 [L_i,R-i]，把询问查询 \(R_i\le r,t\in T_i\) 的区间能覆盖的 \(\min l\)，可以树套树解决。

再解决不跨过区间的。大概扫描线之后线段树维护云云即可。

P11367

对序列分治，跨过区间的点对可以拆为两边到中心，这样就降低了问题的维度（？）。具体地说，对两边分别扫描，需计算值相邻数（如果在 \(i,j\)）贡献。如果已知左端点，判断是否中间被另外一边的数界开，如果是贡献为 \(|2mid-i-j|\)，否则贡献是 \(|i-j|\)，这个左端点分界显然是区间，扫描线的时候加减贡献之类即可。最后是 \(O(n\log^2n)\)，据有人说可以 \(/\log\log n\)。

P7220

题面略

不带加点是可以维护当前的至少被修改一次的点的阶梯型，这是有序的。带加点的问题是可以线段树分治或者二进制分组来避开。

UOJ218

可能考虑换维扫描线，但是强制在线，然而只需查询单点弹出的新栈顶，而我可以维护可持久化来查询上次被覆盖的时间的这个位置的值。

Day4

AT_cf17_final_j

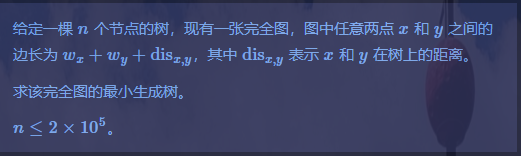
Boruvka，之后在换根 dp 计算每个点到的最小次小（依不同颜色分开）之后连边。是 \(O(n\log n)\)。

P10786

百万富翁。

直接对分组 dp。一个事情是分组的剩余需要扔进老的组里面不能新开或者用 dp 数组之类，否则确实是不优的（也不易实现）。可以整除分块优化 dp。

UOJ52

对于两个序列的问题，需要找到第 \(k\) 小，则在两个序列找到第 \(k/2\) 小，舍去小的那一部分 \(k/2\)，这样实现了二分。三个序列取 \(k/3\) 即可。

P8984

首先需要知道它在说什么。一个区间 \([l,r)\) 对应 \(A_{l,r}\)，要求任意区间分治拆成 \(k\) 个或以下被预处理的区间，然后预处理的区间必须被分治得到，不多于 \(m\) 个。

\(k=2\) 即猫叔分治，\(k=3\) 即分块，预处理任何两块间贡献，以及一块的前缀后缀，然后递归进子问题，获得 \(O(n\log\log n)\) 复杂度。最终 \(k=\log n\) 就是线段树。

\(k=4\) 可以把中间的块间询问转为猫叔分治。进一步地，把问题变为：

分成若干块，块内是子结构，左右两块必须处理前缀/后缀，中间块必须处理前缀和后缀，对于块的整体还需以 \(k-2\) 回答询问，可以 dp。

U474561

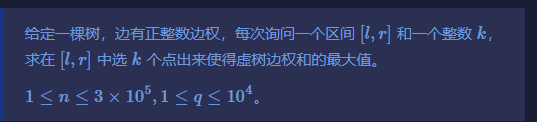
假装这个问题可以贪心，然后定长分块，对 \(n/k\) 个点线段树，这样平衡了修改查询（？）。

P11621

差分，每个三角形现在贴 \(y\)，每个询问现在询问右上角。依靠修改位置关系（右上/半右下）分类修改，可以拆开修改贡献，类的内部是三维偏序，可以 \(O(n\log^2n)\) 解决。

P8259

本质上和上面差不多，但是构式程度翻倍了。

Day5

P5047

区间逆序对。

莫队二离后利用 \(O(\sqrt n)-O(1)\) 分块来平衡修改和多次询问复杂度做到 \(O(n\sqrt n)\)。

P6774

求下标、值域区间给定时区间逆序对数。

对平面分治，这样的好处在于划分为四块之后斜对面的贡献简单。可惜四分树是假的，采取树套树结构。

先考虑如何计算树套树结点答案。树套树结构提供了左右上下四个半块的答案，这样可以直接容斥计算了。

把询问拆出 \(O(\log^2n)\) 个点，算答案：相当于在 \(O(\log n)\) 个树套树点（？）做区间逆序对，直接做可以发现获得 \(O(n\sqrt n)\) 的复杂度。

P5612

颜色段 01-trie 维护，段内可以打标记。区间打标记的话用外层搞个大线段树处理标记下传问题即可。最终复杂度还是 \(O(n\log n)\)，换成压缩 01-trie 获得 \(O(n)\) 空间。

P3316

尝试射线法，把线段插入树套树结构，多边形的好性质是线段不在端点外相交因此一个内层树内线段具有上下关系我直接二分即可。

题目

这个好处是贡献可以分开，不是询问 min。还是考虑两条横线段在树套树结构上的表现：不会相交，只会包含。因此分两类贡献，询问包含修改，修改包含询问。这两类都可以在内层树上完成。

P11370

多次询问多边形边和查询线段是否相交。

算是把上面两题结合起来了，有题解。