线性代数学习笔记一

第一章 线性代数中的线性方程组

1. 线性方程
   包含变量\(x_1,x_2,\cdots,x_n\)的线性方程是形如$$a_1x_1+a_2x_2+\cdots+a_nx_n=b$$的方程，其中\(b\)与系数\(a_1,a_2,\cdots,a_n\)是实数或复数，通常是已知数。

2. 线性方程组
   线性方程组是由一个或几个包含相同变量\(x_1,x_2,\cdots,x_n\)的线性方程组成的。例如

   \[2x_1-x_2+1.5x_3= 8 \]
   \[x_1-4x_3=-7 \]
   • 线性方程组的解是一组数(\(s_1,s_2,\cdots,s_n\))，用这组数分别代替\(x_1,x_2,\cdots,x_n\)时，可使方程组成立。
   • 方程组所有可能的解的集合称为线性方程组的解集，若两个线性方程组有相同的解集，这两个线性方程组称为等价的。
   • 线性方程组的解有以下几种情况：
     1. 无解。
     2. 有唯一解。
     3. 有无穷多解。

3. 矩阵记号
   一个线性方程组的主要信息可以用一个称为矩阵的阵列来表示，给出方程组

\[x_1-2x_2+x_3 = 0 \]

\[2x_2 - 8x_3 = 8 \]

\[5x_1 - 5x_3 = 10 \]

把每一个变量的系数写在对齐的一行中，矩阵：

\[\left[ \begin{array}{ccc} 1 & -2 & 1\\ 0 & 2 & -8\\ 5 & 0 & -5\\ \end{array} \right]\]

称为方程组的系数矩阵，而

\[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\\ 0 & 2 & -8 & 8\\ 5 & 0 & -5 & 10\\ \end{array} \right]\]

称为它的增广矩阵，其实就是把系数矩阵添上一列右边的常数所得。
矩阵的维数说明它包含的行数和列数，上面的增广矩阵有3行4列，称为3×4矩阵，\(m\)×\(n\)矩阵是一个有\(m\)行\(n\)列的数的矩形阵列
4. 解线性方程组
用来化简线性方程组的三种基本变换是：把某个方程换成它与另一方程的倍数的和；交换两个方程的位置；把某一方程的所有项乘以一个非零常数。
接下来我会说明如何利用这三种基本变换来解线性方程组
给出一线性方程组：$$x_1-2x_2+x_3 = 0$$$$2x_2 - 8x_3 = 8$$$$5x_1 - 5x_3 = 10$$
表示出其对应的增广矩阵：

\[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\\ 0 & 2 & -8 & 8\\ 5 & 0 & -5 & 10\\ \end{array} \right]\]

首先，我们要保留第一个方程中的\(x_1\)，把其他方程中的\(x_1\)消去。为此，把第一个方程乘以-5，同第三个方程相加，并用得到的新方程代替第三个方程
即$$x_1-2x_2+x_3 = 0$$$$2x_2-8x_3 = 8$$$$10x_2-10x_3 = 10$$
增广矩阵为

\[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\\ 0 & 2 & -8 & 8\\ 0 & 10 & -10 & 10\\ \end{array} \right]\]

现在我们将方程二乘以二分之一，再将方程三乘以十分之一即

\[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\\ 0 & 1 & -4 & 4\\ 0 & 1 & -1 & 1\\ \end{array} \right]\]

现在我们用方程二减去方程三，并将新得到的方程乘以负三分之一得到：

\[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\\ 0 & 1 & -4 & 4\\ 0 & 0 & 1 & -1\\ \end{array} \right]\]

现在矩阵变成了一个阶梯形（这个形式很重要啊）
接下来我们继续化简，用方程三消除方程一中的\(x_3\)，可得到：

\[\left[ \begin{array}{cccc} 1 & -2 & 0 & 1\\ 0 & 1 & -4 & 4\\ 0 & 0 & 1 & -1\\ \end{array} \right]\]

用方程三消除方程二中的\(x_3\):

\[\left[ \begin{array}{cccc} 1 & -2 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & -1\\ \end{array} \right]\]

最后用方程二消除方程一中的\(x_2\)：

\[\left[ \begin{array}{cccc} 1 & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & -1\\ \end{array} \right]\]

我们将其重新写回方程组的形式：

\[x_1 = 1 \]

\[x_2 = 0 \]

\[x_3 = -1 \]

我们可以得出方程组的解集为（1，0，-1）

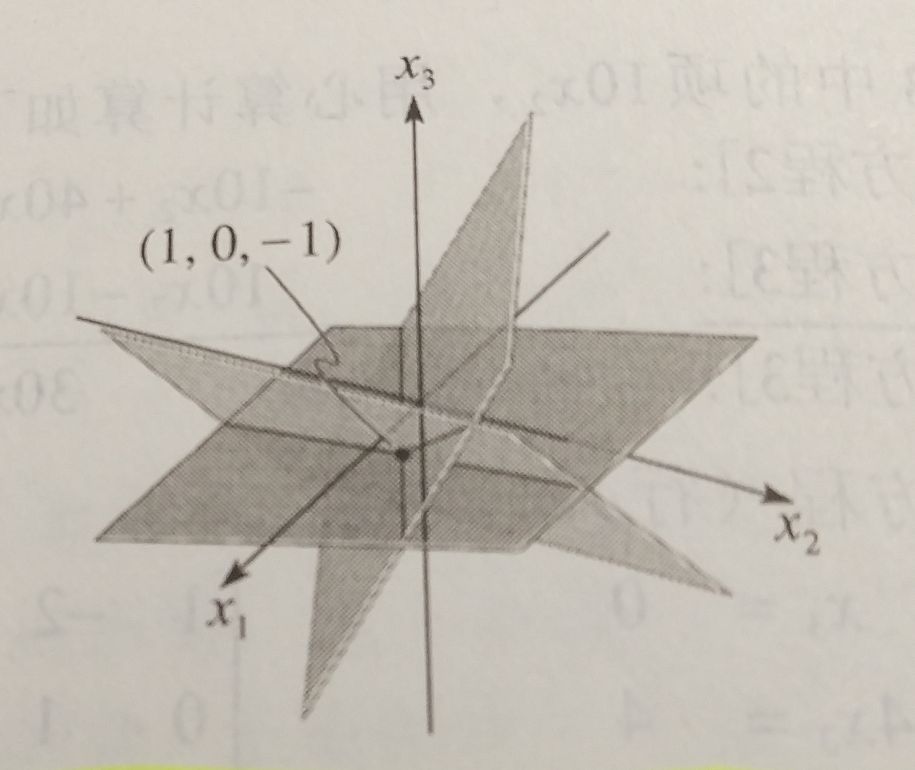
值得一提的是，方程组中每一个方程确定一个平面，而方程组的解集为三个平面的交点.
结合我们之前提到的方程组的解的情况，可知：
1.当方程组有唯一解时，三个面交于同一点。
2.当方程组有无穷多解时，三个面交于同一条直线。
3.当方程组无解时，三个面无共同交点。
5. 行变换
前面所讲的三种基本变换对应于增广矩阵的下列变换
1. （倍加变换）把某一行换成它本身与另一行的倍数的和。
2. （对换变换）把两行对换。
3. （倍乘变换）把某一行的所有元素乘以同一个非零数。

• 行变换可施与任意矩阵。
• 若其中一个矩阵可以经一系列初等行变换成为另一个矩阵，我们称这两个矩阵为行等价的。且行变换可逆。
• 若两个线性方程组的增广矩阵是行等价的，则它们具有相同的解集。

5. 存在性与唯一性问题
   一个线性方程组的解集可能不包含任何解、一个解或无穷多个解。为确定方程组的解集属于那种情况，我们提出以下的问题：
   线性方程组的两个基本问题
   1. 方程组是否有解，即它是否至少有一个解？
   2. 若它有解，她是否只有一个解，即解是否唯一？
   第一个问题很好解决，只要在行变换时发现有矛盾的等式，即可证明是否至少有一个解。
   第二个问题，须先将增广矩阵化为阶梯形，这时最后一行的\(x_n\)已经被确定，层层上代就可以确定其他变量的值。

参考文献：线性代数及其应用 【美】David C.Lay