理解连续分级概率评分 (CRPS)[转译]

转译自：https://www.lokad.com/continuous-ranked-probability-score

最初由 Joannes Vermorel 于 2016 年 6 月编写。
由 Alexey Tikhonov 于 2024 年 5 月更新。

概率预测为每一个可能的未来分配一个概率。然而，所有概率预测的准确性并不相同，因此需要指标来评估不同概率预测的准确性。诸如 MAE（平均绝对误差）或 MAPE（平均绝对百分比误差）等简单的准确性指标不能直接应用于概率预测。连续排序概率评分（CRPS）将 MAE 推广到了概率预测的情况。与交叉熵一起，CRPS 是涉及概率预测时最广泛使用的准确性指标之一。

概述

CRPS 常用于评估两个概率预测模型的准确性。特别地，该指标可以与回测过程结合使用，通过在相同数据集上进行多次测量来稳定准确性评估。

该指标显著不同于如 MAE 等更简单的指标，因为它具有非对称表达：预测是概率性的，而观测是确定性的。与分位点损失函数不同，CRPS 不专注于概率分布的某一点，而是整体考虑预测的分布。

正式定义

设 \(X\) 是一个随机变量。

设 \(F\) 为随机变量 \(X\) 的累积分布函数（CDF），即 \(F(y)=\mathbf{P}[X \leq y]\)。

设 \(x\) 为观测值，\(F\) 为与经验概率预测相关的累积分布函数。

\(x\) 与 \(F\) 之间的连续排序概率分数（CRPS）定义为：

\[CRPS(F, x) = \int_{-\infty}^{\infty}(F(y)- \mathbb{1}(y - x))^2dy \tag{1} \]

其中 \(\mathbb{1}\) 是 Heaviside 阶跃函数，表示沿实数轴的阶跃函数，其取值为：

• 如果实数参数为正或零，则值为 1，
• 否则值为 0。

CRPS 的单位与观测变量相同（例如，如果产品的需求以单位预测，CRPS 也将以单位表示）。

CRPS 是平均绝对误差（MAE）的推广。事实上，如果预测是确定性的，CRPS 将退化为 MAE。下方图表 D 中展示了这一点。

已知属性

Gneiting 和 Raftery (2004) 证明连续排序概率得分可以等价地写成：

\[CRPS(F,x) = \mathbf{E}[|X - x|]-\frac{1}{2}\mathbf{E}[|X - X^*|] \tag{2} \]

其中

• \(X\) 和 \(X^*\) 是线性随机变量的独立副本，
• \(X\) 是与累积分布函数 \(F\) 相关的随机变量，
• \(\mathbf{E}[X]\) 是 \(X\) 的期望值。

数值评估

从数值角度来看，计算 CRPS 的一种简单方法是将原始积分分解为两个在精心选择边界上的积分，以简化 Heaviside 阶跃函数，其表达式为：

\[CRPS(F, x) = \int_{-\infty}^x F(y)^2dy + \int_x^{\infty}(F(y)- 1)^2dy \tag{3} \]

在实践中，由于 \(F\) 是通过预测模型获得的经验分布，相应的随机变量 \(X\) 具有紧支集，意味着只有有限多个点满足 \(\mathbf{P}[X = x] > 0\)。此外，所有 \(x\) 的取值均为离散数值。因此，积分可以转化为离散的有限求和，如下公式及下一节的图表 B 所示。

\[CRPS(F, x) = \sum_{k = 0}^x F(y_k)^2 + \sum_{x + 1}^{n} (F(y_k) - 1)^2 \tag{4} \]

在公式（4）中，索引 \(n\) 表示概率分布右尾的最后一个元素（例如具有非零概率的最高需求值）。

最后，由于 CRPS 计算是针对一个时间点进行的，为了计算特定评价期（例如责任窗口，即供应商提前期和再订货周期的和）内的 CRPS，应对该期间内计算的各个 CRPS 值取平均。

\[CRPS = \frac{1}{T} \sum_{t = 1}^{T} CRPS_t \tag{5} \]

视觉直观

为了说明 CRPS 的计算，请参考以下示例（参见下方图表）：

A：最初，我们使用负二项分布构建了一个概率需求预测，并截断了概率低于 0.1% 的尾部（这些代表极不可能发生的事件，比如大约每三年一次的事件）。预测需求值的非零概率范围从 1 到 26 个单位。后来实际需求被证明是 15 个单位（如垂直红色虚线所示）。

B：我们根据上面第 4 个公式计算了 CRPS（见“数值评估”）。得到的 CRPS 值表示两个用浅红色填充的区域之和。

C：与图表 A 相同，但增加了一个点预测以进行比较。

D：将 CRPS 计算应用于点预测表明，当 CRPS 应用于点预测时，结果是 MAE 准确度指标。实际上，点预测是概率预测的简化形式，我们隐含地将 100%的概率赋予单一值。然后，CRPS 的累计概率图将由两个阶梯函数表示——一个用于点预测，另一个用于实际需求。这意味着，取决于点预测与实际值的相对位置，CRPS 公式（4）中的两个求和项之一将变为零：第一个求和项对应过度预测，第二个求和项对应预测不足。

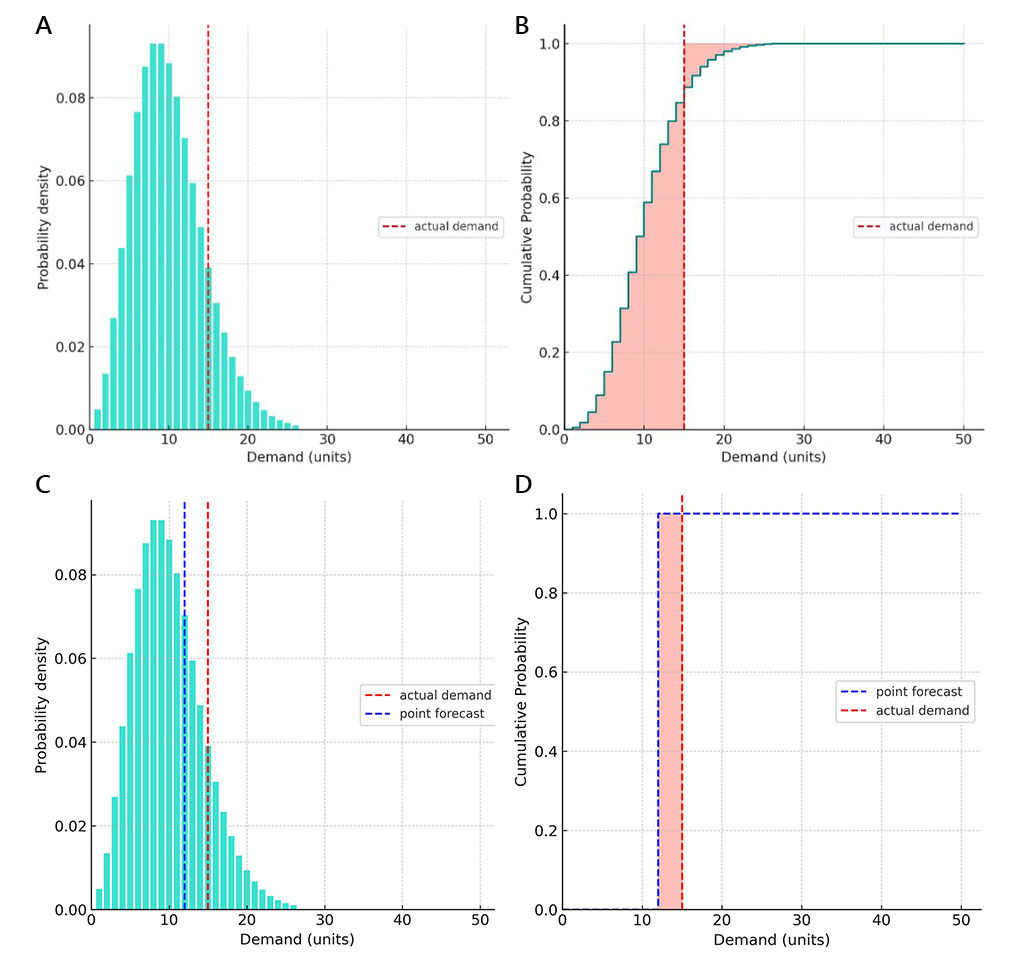
A：概率预测。 B：CRPS。 C：概率预测与点预测。 D：点预测的 CRPS 是 MAE。

对于通过这 4 个图表提供的示例，概率预报和点预报的最终 CRPS 值分别为 3.32 和 3。从数值上看，人们可能会认为点预报更准确，因为它的准确性指标比概率预报的小（更好）。然而，这个结论是错误的。

在上述示例中，我们只考虑了一个实际需求值，然而当概率预测是通过历史数据学习时，概率会根据各自需求值出现的频率进行调整（考虑学习数据集中可用的值）。如果选择得当，那么测试数据集的平均 CRPS 值将与训练/验证数据集的 CRPS 值相当，因为该预测能够充分代表测试数据中不同需求值的出现频率。

下图展示了概率预测相对于点预测的优越性。

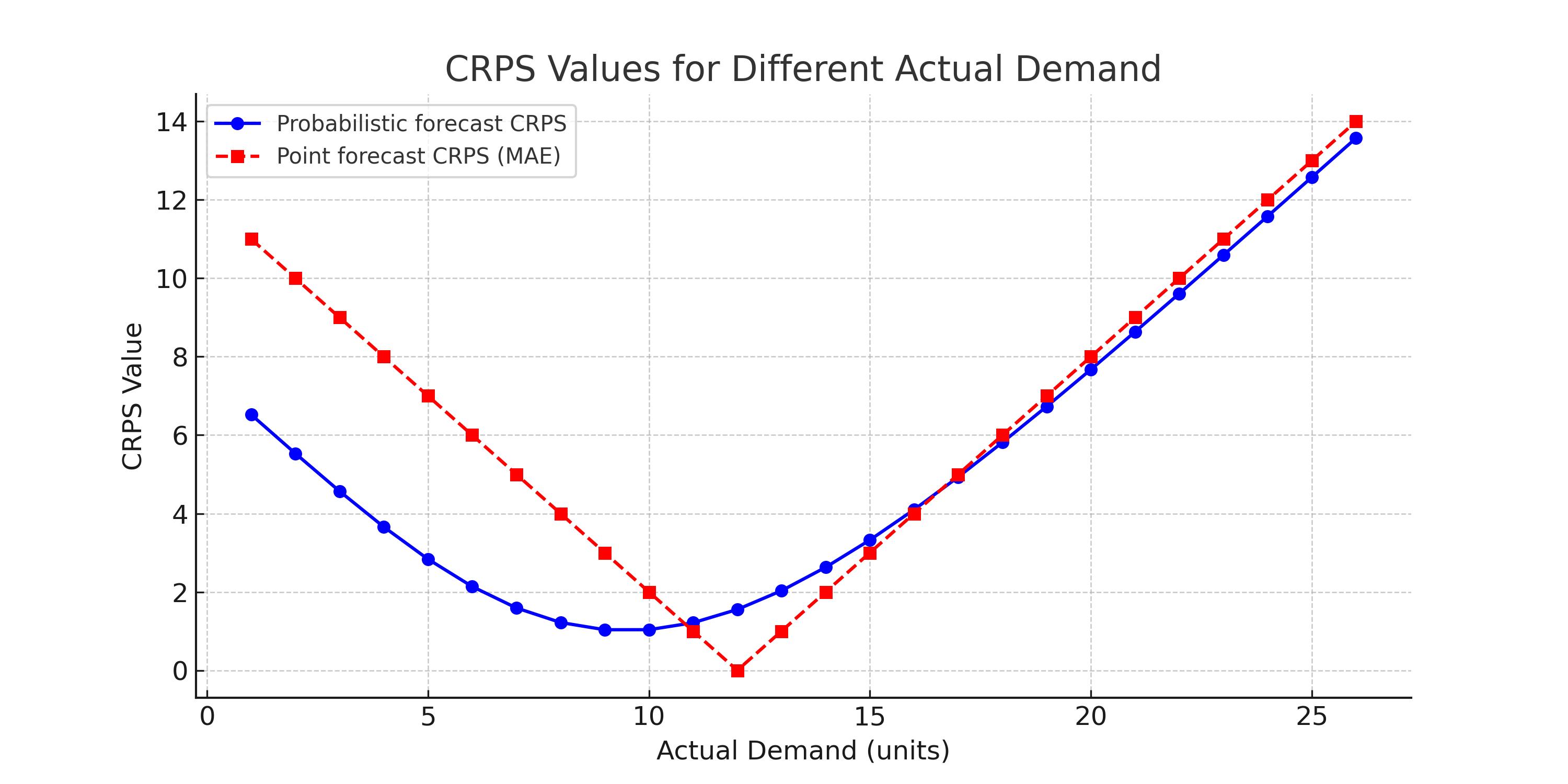
请注意 CRPS 随不同实际值变化的平滑程度。还要注意，除了一个很小的区域（点预测非常接近实际值），在所有其他区域，概率预测的 CRPS 都小于点预测的 CRPS。

如果我们有多个不同的点预测，这一观察结果依然成立。人们只需根据点预测在脑海中将红色曲线向左或向右移动，但概率预测的优越性依然有效。

参考文献

Gneiting, T. and Raftery, A. E. (2004). Strictly proper scoring rules, prediction, and estimation. Technical Report no. 463, Department of Statistics, University of Washington, Seattle, Washington, USA.