作业 03 - 深层神经网络

深层神经网络

最重要的是要让整个过程向量化以加快运行速度，这里给出矩阵的大小.    

假设一共有 $\mathrm{L}$ 层，$\mathrm{m}$ 个训练样本，每一层的节点数量为 $\mathrm{n[l]}$        

$\mathrm{W[l] = (n[l], n[l - 1])}$, $\mathrm{b[l] = (n[l], 1)}$, $\mathrm{Z[l] = A[l] = (n[l], m)}$     

正向传播公式

$\mathrm{Z[l] = W[l]A[l - 1] + b[l]}$, $\mathrm{A[l] = g(Z[l])}$

反向传播公式

注：在 $\mathrm{A[L]}$ 对 $\mathrm{Cost}$ 求导时没有算进 $\mathrm{\frac{1}{m}}$

根据后续的需要进行的除法.   

$\mathrm{d(Z[l])=d(A[l]) * g[l]'(Z[l])}$

$\mathrm{d(W[l]) = \frac{1}{m} d(Z[l]) A[l - 1] ^{T}}$ 

$\mathrm{d(b[l]) = \frac{1}{m} np.sum(d(Z[l]), axis=1, keepdims=True)}$ 

$\mathrm{d(A[l - 1]) = W[l] ^T d(Z[l])}$ 

代码

这份代码里封装了 $\mathrm{ANNs}$ 函数，只需要输入每一层的节点数量，激活函数类型，程序就会根据训练数据学习.  

最佳的参数需要自己一步一步去调，同时学习次数不宜过多防止过拟合的事情发生.  

学习效果：

 

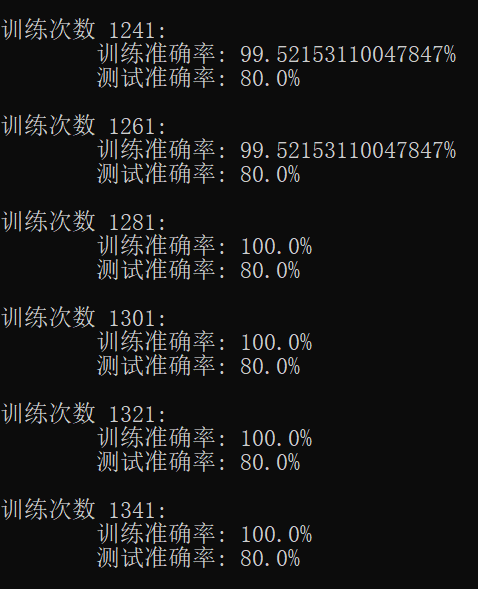
调用代码：

from inspect import Parameter
import numpy as np
import h5py
import matplotlib.pyplot as plt
from lr_utils import load_dataset   
from beta import ANNs, calculate  
train_x, train_y, test_x, test_y, classes = load_dataset() 
train_x = train_x.reshape(train_x.shape[0], -1).T / 255
test_x  = test_x.reshape(test_x.shape[0], -1).T   / 255

X , Y = train_x, train_y

acti = ["ng", "relu",  "relu", "relu", "sigmoid"]   

layer = [X.shape[0], 20, 20, 5, 1]      

ANNs(X, Y, test_x, test_y, layer, acti, 10000, 0.0075)   

　　

$\mathrm{ANNs}$ 代码

import numpy as np
import matplotlib.pyplot as plt
import h5py 

def sigmoid(x):  
    return 1.0 / (1.0 + np.exp(-x))   

def dsigmoid(y):  
    return y * (1 - y)        

def relu(x):  
    return np.maximum(0.0, x)    

def drelu(y): 
    return (y > 0).astype('int')  

def tanh(x):  
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))  

def dtanh(y):
    return 1 - np.power(y, 2)

# 随机初始化 W, b 的值.      

def initialize(layer_dims):  
    np.random.seed(2)  
    L = len(layer_dims)  
    parameters = {}  
    for l in range(1, L): 
        parameters["W" + str(l)] = np.random.randn(layer_dims[l], layer_dims[l - 1]) / np.sqrt(layer_dims[l - 1])
        parameters["b" + str(l)] = np.random.randn(layer_dims[l], 1) * 0.01       
    return parameters   

# 向前函数.  

def linear_forward(A_prev, W, b):   
    """
    计算出导出的 z[l] 

    cashe[0] = A_prev 

    cashe[1] = W 

    cashe[2] = b 

    cashe 保存 (A_prev, W, b)

    """  

    z = np.dot(W, A_prev) + b

    cashe = (A_prev, W, b) 
    return z, cashe 

def forward(A_prev, W, b, activation_type):  
    """
    返回：

    A[l] 

    g[l]'(z[l])  

    z[l]  

    linear_cashe
    
    """
    z, linear_cashe = linear_forward(A_prev, W, b)        
    if activation_type == "sigmoid":      
        A_nex = sigmoid(z)
        delta = dsigmoid(A_nex)  
    if activation_type == "relu":  
        A_nex = relu(z)  
        delta = drelu(A_nex)  
    if activation_type == "tanh":  
        A_nex = tanh(z)   
        delta = dtanh(A_nex) 
    return A_nex, delta, z, linear_cashe  

def backward(dAL, delta, z, linear_cashe):   
    dZL = dAL * delta  
    dWL = (1 / dAL.shape[1]) * np.dot(dZL, linear_cashe[0].T)            
    dbL = (1 / dAL.shape[1]) * np.sum(dZL, axis = 1, keepdims = True)   
    dA_prev = np.dot(linear_cashe[1].T, dZL)               
    return dZL, dWL, dbL, dA_prev  

def calculate(X, parameters, layer_type):  

    L = len(layer_type)     
    A = X  
    for i in range(1, L):   
        A = np.dot(parameters["W" + str(i)], A) + parameters["b" + str(i)]   
        if layer_type[i] == "sigmoid": 
            A = sigmoid(A)  
        if layer_type[i] == "relu":  
            A = relu(A)  
        if layer_type[i] == "tanh":  
            A = tanh(A)  
    return A  

# 输入训练数据与测试数据方便监测学习过程.  

def ANNs(X, Y, tx, ty, layer_dims,acti_type,steps = 1000, lr = 0.09):  

    parameters = initialize(layer_dims)     
    # data 用来存储数据       
    for i in range(steps):      
        A = X  
        L = len(layer_dims)   
        data = []  
        data.append(())  
        for l in range(1, L):             
            A_nex,delta,z,linear_cashe = forward(A, parameters["W"+str(l)], parameters["b"+str(l)], acti_type[l])   
            data.append((A_nex, delta, z, linear_cashe))    
            A = A_nex   

        dAL = -(Y/(A + 1e-9)) + (1 - Y) / (1 - A + 1e-9)         

        for l in range(L - 1, 0, -1):     
            dZL, dWL, dbL, dA_prev = backward(dAL, data[l][1], data[l][2], data[l][3])        
            parameters["W" + str(l)] -= lr * dWL   
            parameters["b" + str(l)] -= lr * dbL   
            dAL = dA_prev    
        
        # 每隔 20 次输出正确率.  
        if i % 20 == 0:  
            cc = 0  
            z = (calculate(X, parameters, acti_type) >= 0.5).astype('int')   
            for j in range(Y.shape[1]):  
                if z[0][j] == Y[0][j]:   
                    cc = cc + 1        
            z = (calculate(tx, parameters, acti_type) >= 0.5).astype('int')  
            pp = 0 
            for j in range(ty.shape[1]):  
                if z[0][j] == ty[0][j]:  
                   pp = pp + 1  
            print("训练次数 " + str(i + 1) + ": ")  
            print("        训练准确率: " + str(cc / Y.shape[1] * 100) + "%")
            print("        测试准确率: " + str(pp / ty.shape[1] * 100) + "%")      
            print("")    
   
    return parameters