作业 02 - 双层神经网络实现分类

双层神经网络

作业 01 只用了单层神经网络实现分类，这次用单隐藏层神经网络来实现

注：$\mathrm{\times}$ 代表正常的矩阵乘法，$\mathrm{*}$ 代表数乘或者矩阵对应位置相乘.   

输入 $\mathrm{m}$ 个训练样本，每个样本有 $\mathrm{n[0]}$ 个特征

正向传播递推式

$\mathrm{X=(n[0], m)}$, 

$\mathrm{w1 = (n[1], n[0])}$, $\mathrm{b1 = (n[1], 1)}$, $\mathrm{w2 = (1, n[1]), b2 = (1, 1)}$   

$\mathrm{z1 = w1 \times X + b1}$, $\mathrm{a1 = tanh(z1)}$    

$\mathrm{z2 = w2 \times a1 + b2}$, $\mathrm{a2 = sigmoid(z2)}$  

反向传播递推式

$\mathrm{d(z2) = [a2[1] - Y[1], a2[2] - Y[2]......a2[m] - Y[m]]}$

$\mathrm{d(w2) = \frac{1}{m} d(z2) \times A^{T}}$  

$\mathrm{d(b2) = \frac{1}{m} np.sum(d(z2), axis=1,keepdims=True)}$

$\mathrm{d(z1) = \frac{1}{m} (w2)^{T} \times d(z2) * tanh'(z1)}$   

$\mathrm{d(w1) = \frac{1}{m} d(z1) X^{T}}$    

$\mathrm{d(b1) = \frac{1}{m} np.sum(d(z1), axis=1,keepdims=True)}$  

 源自 Andrew Ng 的 PPT 

代码实现 

import numpy as np
import h5py
import matplotlib.pyplot as plt
from lr_utils import load_dataset 
 
def sigmoid(x):
    return 1 / (1.0 + np.exp(-x))  

def tanh(x):  
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x)) 

def dtanh(y):
    return 1 - (y * y)      

def neural_solve(train_x, train_y, n1, step = 100, lr = 0.009):    
    n0, m = train_x.shape   
    #w1, b1 = np.random.randn(n1, n0) * (1 / np.sqrt(m)), np.random.randn(n1, 1) * 0.01 
    #w2, b2 = np.random.randn(1, n1) * (1 / np.sqrt(n1)), np.random.randn(1, 1)  * 0.01     
    w1, b1 = np.random.randn(n1, n0) * 0.001, np.random.randn(n1, 1) * 0.01 
    w2, b2 = np.random.randn(1, n1) *  0.5, np.random.randn(1, 1)  * 0.01     
    # w1(n1, n0), b1(n1, 1)   
    # w2(1, n1), b2(1, 1)
    # X(n0, m), Y(1, m)          
    X , Y = train_x, train_y  
    for i in range(0, step + 1):       
        # 这些是向前传播.   
        z1 = np.dot(w1, X) + b1  
        a1 = tanh(z1)         
        z2 = np.dot(w2, a1) + b2    
        a2 = sigmoid(z2)  

        # 向后传播  
        dz2 = a2 - Y  
        dw2 = (1 / m) * np.dot(dz2, a1.T)        
        db2 = (1 / m) * np.sum(dz2, axis = 1, keepdims = True) 

        dz1 = (1 / m) * np.dot(w2.T, dz2) * dtanh(a1)      
        dw1 = (1 / m) * np.dot(dz1, X.T)  
        db1 = (1 / m) * np.sum(dz1, axis = 1, keepdims = True)             

        w1 -= lr * dw1  
        b1 -= lr * db1  
        w2 -= lr * dw2  
        b2 -= lr * db2     

    return w1, b1, w2, b2  

def calculate(X, w1, b1, w2, b2):  
    z1 = np.dot(w1, X) + b1
    a1 = tanh(z1) 
    z2 = np.dot(w2, a1) + b2    
    a2 = sigmoid(z2)   
    return a2 

　　

第二周作业

用双层神经网络实现对于猫的识别，训练数据正确率达到 $0.9$ 时测试数据达到了 $0.74$ 的正确率.    

这里隐藏层开了 3 个节点. 

import numpy as np
import h5py
import matplotlib.pyplot as plt
from lr_utils import load_dataset 
 
def sigmoid(x):
    return 1 / (1.0 + np.exp(-x))  

def tanh(x):  
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x)) 

def dtanh(y):
    return 1 - (y * y)      

def neural_solve(train_x, train_y, n1, step = 100, lr = 0.009):    
    n0, m = train_x.shape   
    #w1, b1 = np.random.randn(n1, n0) * (1 / np.sqrt(m)), np.random.randn(n1, 1) * 0.01 
    #w2, b2 = np.random.randn(1, n1) * (1 / np.sqrt(n1)), np.random.randn(1, 1)  * 0.01     
    w1, b1 = np.random.randn(n1, n0) * 0.001, np.random.randn(n1, 1) * 0.01 
    w2, b2 = np.random.randn(1, n1) *  0.5, np.random.randn(1, 1)  * 0.01     
    # w1(n1, n0), b1(n1, 1)   
    # w2(1, n1), b2(1, 1)
    # X(n0, m), Y(1, m)          
    X , Y = train_x, train_y  
    for i in range(0, step + 1):       
        # 这些是向前传播.   
        z1 = np.dot(w1, X) + b1  
        a1 = tanh(z1)         
        z2 = np.dot(w2, a1) + b2    
        a2 = sigmoid(z2)  

        # 向后传播  
        dz2 = a2 - Y  
        dw2 = (1 / m) * np.dot(dz2, a1.T)        
        db2 = (1 / m) * np.sum(dz2, axis = 1, keepdims = True) 

        dz1 = (1 / m) * np.dot(w2.T, dz2) * dtanh(a1)      
        dw1 = (1 / m) * np.dot(dz1, X.T)  
        db1 = (1 / m) * np.sum(dz1, axis = 1, keepdims = True)             

        w1 -= lr * dw1  
        b1 -= lr * db1  
        w2 -= lr * dw2  
        b2 -= lr * db2     

    return w1, b1, w2, b2  

def calculate(X, w1, b1, w2, b2):  
    z1 = np.dot(w1, X) + b1
    a1 = tanh(z1) 
    z2 = np.dot(w2, a1) + b2    
    a2 = sigmoid(z2)   
    return a2 

train_x, train_y, test_x, test_y, classes = load_dataset() 

train_x = train_x.reshape(train_x.shape[0], -1).T / 255        
test_x  = test_x.reshape(test_x.shape[0], -1).T   / 255    

cases = test_y.shape[1]  

w1, b1, w2, b2 = neural_solve(train_x, train_y, 3, 9000, 0.008)   
        
answer = calculate(test_x, w1, b1, w2, b2) >= 0.5  

answer_test = calculate(train_x, w1, b1, w2, b2) >= 0.5 


# print(answer) 
"""
for i in range(cases):    
    print((int)(answer[0][i]), test_y[0][i])   
"""

dd = 0 
for i in range(train_y.shape[1]):    
    if(answer_test[0][i] == train_y[0][i]) :   
        dd += 1  
print(dd / train_y.shape[1])   

cc = 0 
for i in range(cases):  
    if(answer[0][i] == test_y[0][i]):  
        cc += 1
print(cc / cases)        
  

　　

第三周作业

这次作业是对一个二维图形进行颜色的分类

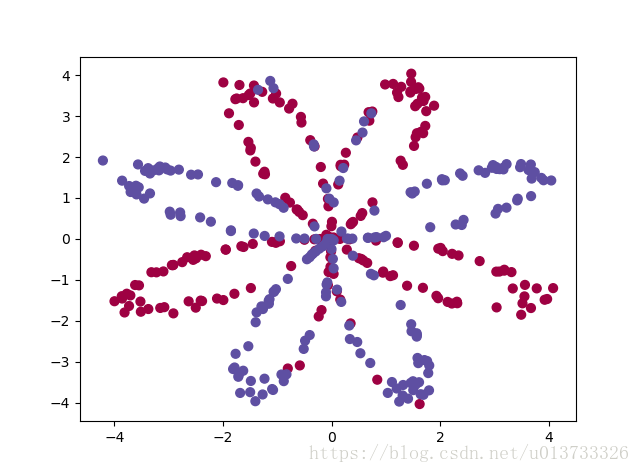
由于颜色的分布并不是线性的，所以直接用一层神经网络是无法完成高正确率的分类的.

即使对训练数据针对大量的训练，模型对于训练数据也只有 50% 的正确率.   

使用双层神经网络可以让正确率提高到 87.5%, 神经网络是自己封装好的，直接调用即可.  

神经网络：

import numpy as np
import h5py
import matplotlib.pyplot as plt 
 
def sigmoid(x):
    return 1 / (1.0 + np.exp(-x))  

def tanh(x):  
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x)) 

def dtanh(y):
    return 1 - np.power(y, 2)       

def neural_solve(train_x, train_y, n1, step = 100, lr = 0.009):  
    np.random.seed(233)   
    n0, m = train_x.shape   
    #w1, b1 = np.random.randn(n1, n0) * (1 / np.sqrt(m)), np.random.randn(n1, 1) * 0.01 
    #w2, b2 = np.random.randn(1, n1) * (1 / np.sqrt(n1)), np.random.randn(1, 1)  * 0.01     
    w1, b1 = np.random.randn(n1, n0) * 0.01, np.random.randn(n1, 1) * 0.01 
    w2, b2 = np.random.randn(1, n1) *  0.01, np.random.randn(1, 1)  * 0.01     
    # w1(n1, n0), b1(n1, 1)   
    # w2(1, n1), b2(1, 1)
    # X(n0, m), Y(1, m)          
    X , Y = train_x, train_y  
    for i in range(0, step + 1):       
        # 这些是向前传播.   
        z1 = np.dot(w1, X) + b1  
        a1 = tanh(z1)         
        z2 = np.dot(w2, a1) + b2    
        a2 = sigmoid(z2)  

        # 向后传播  
        dz2 = a2 - Y  
        dw2 = (1 / m) * np.dot(dz2, a1.T)        
        db2 = (1 / m) * np.sum(dz2, axis = 1, keepdims = True) 

        dz1 = (1 / m) * np.dot(w2.T, dz2) * dtanh(a1)      
        dw1 = (1 / m) * np.dot(dz1, X.T)  
        db1 = (1 / m) * np.sum(dz1, axis = 1, keepdims = True)             

        w1 -= lr * dw1  
        b1 -= lr * db1  
        w2 -= lr * dw2  
        b2 -= lr * db2     

    return w1, b1, w2, b2  

def calculate(X, w1, b1, w2, b2):  
    z1 = np.dot(w1, X) + b1
    a1 = tanh(z1) 
    z2 = np.dot(w2, a1) + b2    
    a2 = sigmoid(z2)   
    return a2 

　　

调用代码

import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
from a import neural_solve, calculate
np.random.seed(1) 

X, Y = load_planar_dataset()

print("X 的形状： " +  str(X.shape))    
print("Y 的形状： " +  str(Y.shape))     

# X[0], X[1] -> Y   

w1, b1, w2, b2 = neural_solve(X, Y, 4 , 40000, 1.2)       

answer = calculate(X, w1, b1, w2, b2) >= 0.5 

cc = 0 

for i in range(400):  
    if answer[0][i] == Y[0][i]:  
        cc += 1

print("训练数据正确率：" + str(cc / 4) + "%")