跟着gpt5学习llama的技术演进——学到了rmsNorm和layerNorm差别，SwiGLU平滑过度，利于信息流正向流动，还有ROPE这种更优雅的相对位置编码

LLaMA系列模型：发展脉络 回顾梳理下技术演进呢
 
 
GPT-5
 
 

当然可以。这是一个非常有意思的话题。LLaMA（Large Language Model Meta AI）系列是 Meta（原Facebook） 在开放大模型生态中非常关键的一条技术路线，它的演进体现了从研究导向的开放模型逐步走向具备商用潜力的通用基础模型的过程。下面我帮你系统梳理一下 LLaMA → LLaMA 2 → LLaMA 3 的发展脉络与技术演进。

一、LLaMA（LLaMA 1，2023年2月）

背景：
当时OpenAI的GPT系列正快速迭代，但大多数模型闭源。Meta试图推动开放研究生态，推出了LLaMA（Large Language Model Meta AI）。

主要特征：

  • 模型规模： 7B、13B、33B、65B 四个版本。
  • 架构： 标准的 Transformer Decoder-only 架构，采用与GPT-3类似的设计。
  • 训练数据： 约1.4T tokens，全部来自公开数据（CommonCrawl、Wikipedia、C4、Books、GitHub等），强调「可复现与开放」。
  • 优化细节：
    • 采用了 RMSNorm（比LayerNorm更高效）；
    • 移除了Position-wise FeedForward中的偏置项；
    • 使用 Rotary Positional Embedding（RoPE）；
    • 较高效的分布式训练技术和数据并行策略。
  • 重要影响：
    尽管官方只面向学术申请开放，但模型权重短暂泄露后广泛传播，直接催生了 Alpaca、Vicuna、Koala 等基于LLaMA微调的开源聊天模型。这实际上开启了“开源大模型时代”。

二、LLaMA 2（2023年7月）

背景：
Meta意识到开源社区活跃度与生态潜能巨大，于是正式推出 LLaMA 2 并开放商用许可。

主要改进：

  • 训练规模更大： 2T tokens（数量翻倍）。
  • 上下文长度： 扩充至4K tokens。
  • 训练策略改进：
    • 更长训练时间与更丰富数据源；
    • 在高质量的多语言、代码数据上加强；
    • 更好的数据清洗与去重质量控制。
  • 引入微调版本：
    • LLaMA 2-Chat：经过“安全+有益”指令微调，采用RLHF（Reinforcement Learning from Human Feedback）管线，是Meta正式提供的对话能力模型。
  • 性能表现：
    • LLaMA 2-70B 能与 GPT-3.5 竞争；
    • 比其他开源模型（如Falcon、MPT）全面领先。
  • 生态意义：
    正式确立Meta“开放但受控”的策略：开放研究 + 可商用 + 健康生态。

三、LLaMA 3（2024年4月）

背景：
AI竞争格局进一步激烈，Meta希望在开放端提供能与GPT-4、Claude 3相匹敌的基座模型，于是发布 LLaMA 3 系列（部分）。

核心创新：

  • 模型规模： 8B、70B 两个版本（当时的第一波发布）。
  • 数据规模与质量：
    • 训练约15T tokens（大幅增加）；
    • 强化代码、数学、推理数据；
    • 引入synthetic（合成）数据与高质量人工过滤数据集；
    • 更全球化的数据分布（多语言、多模态前期实验）。
  • 架构与训练优化：
    • 新的 tokenizer（词表更高效，支持多语言）；
    • 更优的收敛与稳定性技巧；
    • 改进的RoPE缩放策略，提升上下文能力（支持更长输入）。
  • 发布生态：
    • 直接提供API、模型权重、推理服务；
    • 官方Chat版本（LLaMA 3 Chat）在安全性、对齐、风格等方面显著提升；
    • 支持在各种平台（Hugging Face、Ollama、AWS、Azure）直接部署。

研究趋势（展望至 LLaMA 3.1 与 LLaMA 3.2）：

  • 支持更长上下文（>128K tokens）；
  • 更完善的多语言与多模态版本；
  • focus on agentic capabilities（自主任务能力）。

四、总结：演进脉络简表

表格
 
代次时间模型规模训练数据量核心改进点特征定位
LLaMA 1 2023.02 7B–65B ~1.4T tokens 开源基础研究模型 开源里程碑
LLaMA 2 2023.07 7B–70B ~2T tokens RLHF、可商用开放 开源+安全
LLaMA 3 2024.04 8B、70B ~15T tokens 新tokenizer、高质数据、RoPE改进 对标GPT-4级性能

如果你希望我进一步延展，比如：

  • LLaMA与其他开源模型（Mistral、Gemma、Qwen）对比演进，或
  • 从体系角度分析Meta为何坚持“开放可控”路线，

我可以帮你做更深入的技术或战略层分析。你希望深入哪一块？

 
采用了 RMSNorm（比LayerNorm更高效） 展开下呢
 
 
GPT-5
 
 

非常好的问题。RMSNorm 是 LLaMA 系列模型在底层网络结构上一个很重要但常被忽略的细节改进。它看起来像个“小优化”，但对于大规模 Transformer 模型的稳定性、效率和收敛速度，都有显著影响。我们可以从 为什么要改、原理是什么、有什么效果 三个角度来展开。

一、背景：为什么不用 LayerNorm？

Transformer 原始结构（Vaswani 等人的论文 Attention Is All You Need, 2017）使用的是 LayerNorm（层归一化）。

不过，随着模型规模扩大（几十亿、上千亿参数），LayerNorm 会产生一些问题：

  1. 计算负担较重——LayerNorm 要计算每个特征的均值 (mean) 和方差 (variance)，这在分布式训练中代价较高；
  2. 训练不稳定性——在极深或极大的模型中，LayerNorm 的“中心化”（减均值）步骤可能引入数值震荡；==》因为 (x−μ)/σ 这个结果取值范围是 【-无穷，+无穷】
  3. 显存浪费——计算 mean 和 variance 都要保存中间结果，在 GPU 上不太友好。

RMSNorm 是一种 简化但效果相似的归一化方法，它保持了数值稳定性，但去掉了均值操作，从而降低复杂度、提高效率。

 

 

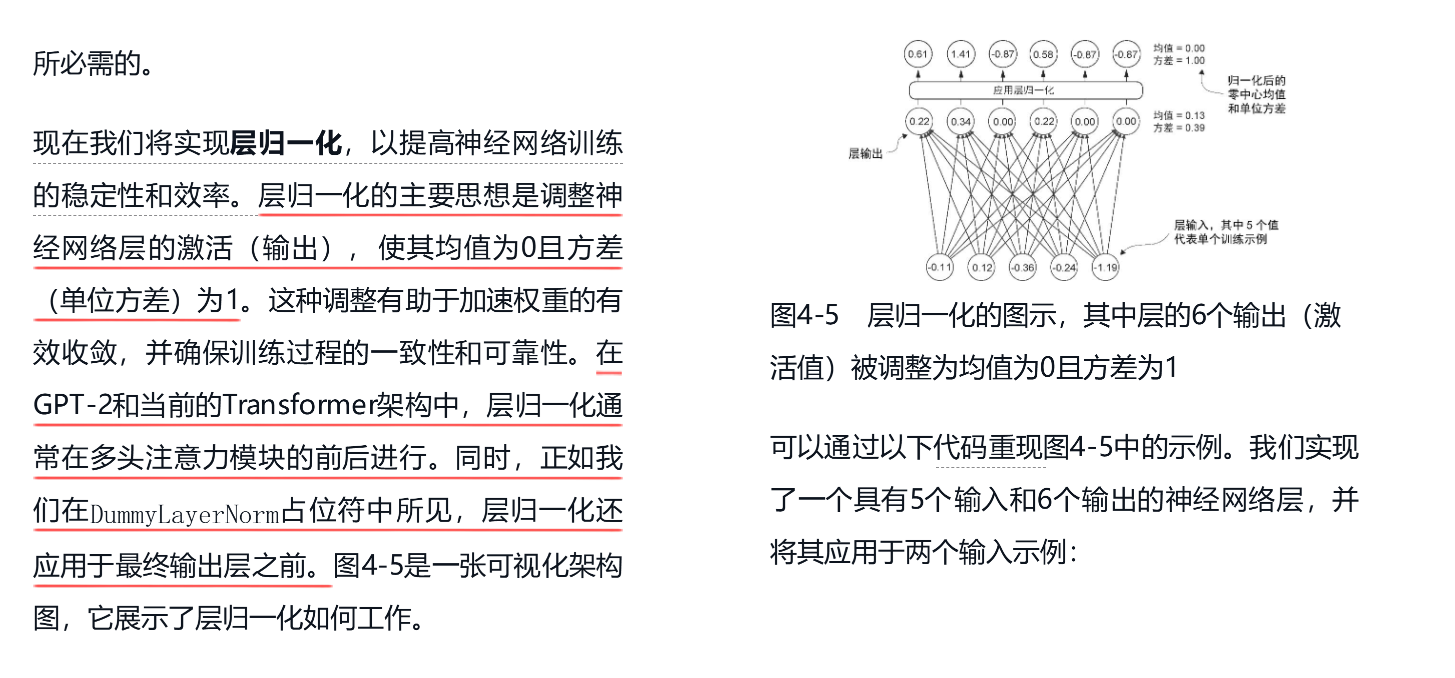
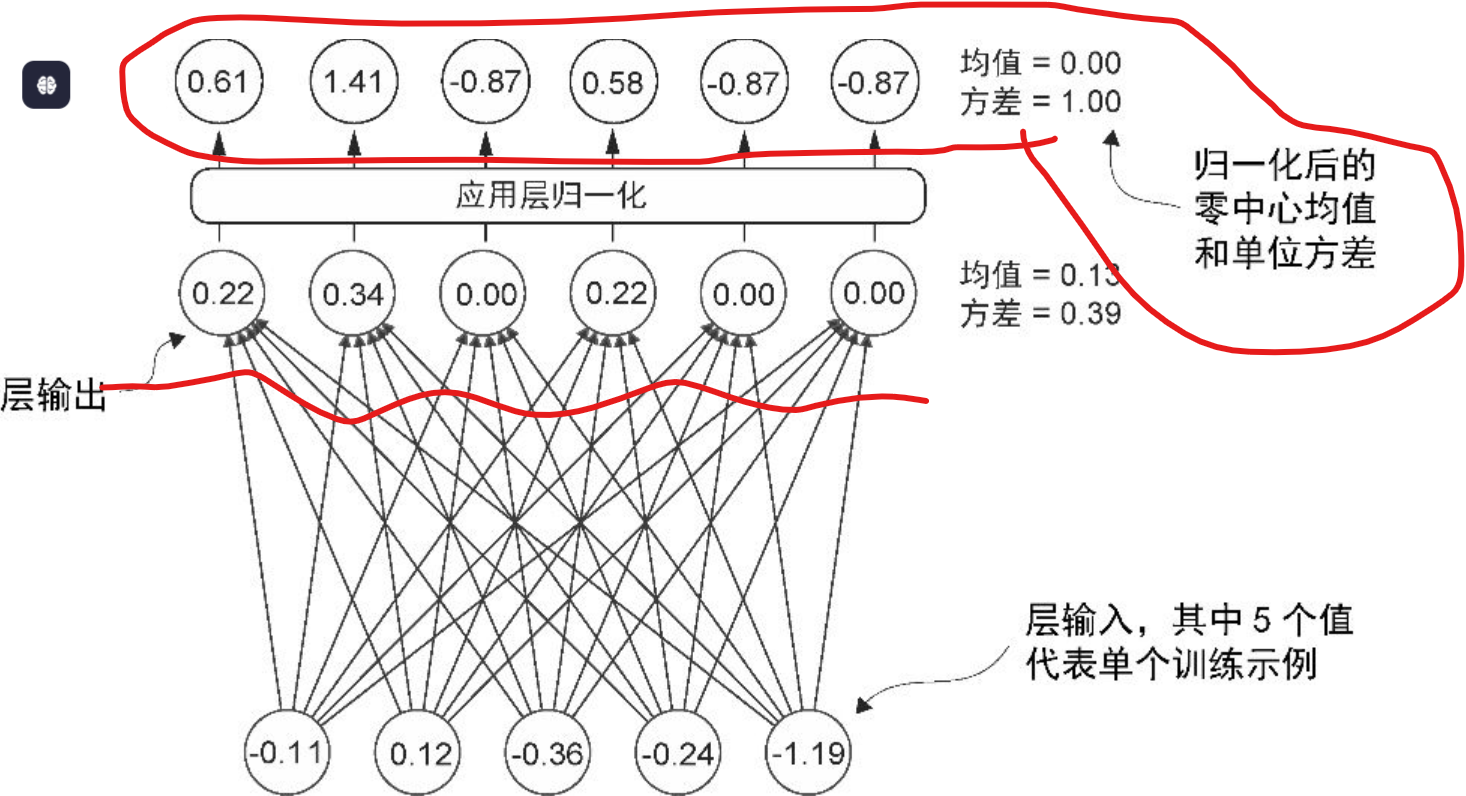
二、原理：RMSNorm 是怎么做的？

我们先看 LayerNorm 的标准公式（针对输入向量 x∈Rdx∈Rd）：

LayerNorm(x)=x−μσ2+ϵ⊙gLayerNorm(x)=σ2+ϵ​x−μ​⊙g

其中：

  • μ=1d∑ixiμ=d1​∑i​xi​（均值），
  • σ2=1d∑i(xi−μ)2σ2=d1​∑i​(xi​−μ)2（方差），
  • gg 是可学习的缩放参数（scale）。

而 RMSNorm (Root Mean Square Normalization) 仅使用平方均值（RMS），不减去均值：==》没有无穷大这样的数，所以其实会更好的！！！

RMSNorm(x)=xRMS(x)⊙g=x1d∑ixi2+ϵ⊙gRMSNorm(x)=RMS(x)x​⊙g=d1​∑i​xi2​+ϵ​x​⊙g

要点有：

  • 不计算均值（μμ）；
  • 只用平方根均方（Root Mean Square）来归一化；
  • 仍有可学习参数 gg 控制缩放强度。

 

 

RMSNorm的优势在于它可以有效地减少模型内部的协变量偏移，加速模型

 

的收敛。同时，由于它只使用RMS进行归一化，可以避免一些不必要的计算，

 

提高模型的效率。此外，RMSNorm还具有线性特征，可以使用部分数据的

 

RMSNorm来代替全部的计算，进一步提高模型的效率。
 

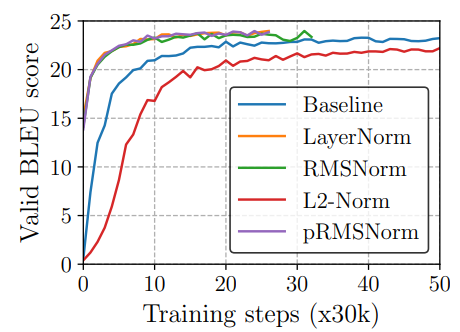
image

 

RMSNorm可在保持模型精度的同时，加速模型收收敛速度

 

三、为什么 RMSNorm 更高效也更稳定？

1. 更低计算成本：

  • 少了一次均值计算（减去 μμ），节省约 30% 的归一化计算时间；
  • 对 GPU/TPU 友好，减少同步开销；

2. 更好的数值稳定性：

  • 不中心化反而减少了梯度在超大网络层间的震荡；
  • 在超大模型（如百亿级参数）中能更容易保持稳定收敛；

3. 更快的训练收敛：

  • 实验表明 RMSNorm 可以带来更快的 early-stage 收敛；
  • 与将 LayerNorm 移到不同位置（如 PreNorm）结合效果更好。

LLaMA、T5、BLOOM、Mistral 等多个现代模型都采用了 RMSNorm 或 PreRMSNorm 结构，已经成为一种“事实上的新标准”。

四、LLaMA 具体实现细节

在 LLaMA 系列的 Transformer block 中，每个子层（自注意力层、MLP层）都采用了 Pre-RMSNorm 形式：

即结构大致为：

ini
 
x = x + MLP(RMSNorm(x)) x = x + Attention(RMSNorm(x))

好处是：

  • 保持梯度稳定；
  • 避免 LayerNorm 的额外开销；
  • 与深层 Transformer（如 65B 以上）配合良好。

✅ 小结：RMSNorm vs LayerNorm 对比

表格
 
特性LayerNormRMSNorm
是否计算均值 ✅ 是 ❌ 否
计算复杂度 相对高 更低
数值稳定性 大模型中较易震荡 更平稳
推理速度 略慢 更快
在大模型中的采纳率 逐步被替代 已成主流

如果你感兴趣，我可以进一步展开：

  • RMSNorm 与其他改进方案（如 ScaleNorm, PowerNorm）的关系；
  • 或是分析它如何与 Pre-Norm Transformer 结构协同起稳定训练作用。

你希望我进一步讲哪一部分？

 
使用 Rotary Positional Embedding（RoPE） ？？？
 
 
GPT-5
 
 

。。。。

换句话说：

不再“加”位置信息，而是让不同位置的向量在特征平面上旋转不同角度。

这个旋转其实是一个复数乘法（因此有时也叫作「Complex Rotation Embedding」）。

 

在二维空间中，存在一个旋转矩阵M(theta)，
当一个二维向量左乘旋转矩阵时，该向量
即可实现弧度为theta的逆时针旋转操作。

 

RoPE旋转位置编码
RoPE不是添加位置向量，而是对词向量应用旋转。旋转角度(θ) 与单词在
句子中的位置成正比，第一个位置的向量旋转θ，第二个位置的向量旋转
2θ，依此类推。因此，只需要将向量旋转某个角度，即可实现对该向量添加
绝对位置信息，并且向量旋转具有周期性，这就是旋转位置编码的由来。
 

 

。

 
 
GPT-5
 
 

非常好的问题 👍。
RoPE 这个东西公式看起来很数学化（“旋转嵌入”、复数乘法之类），但其实本质挺直观的。我们可以用生活化的比喻和图像直觉来理解它，让这些旋转的操作变得有感知。

🌪 一、直觉比喻：让每个词都“转一点角度的风车叶片”

想象这样一个画面：

  • 句子是由一排小风车叶片组成的，
  • 每个风车的中心是这个词的语义向量；
  • 不同的位置（第1个、第2个、第3个……）的风车叶片朝向不同方向——
    越往后，它们被旋转的角度越大。

这样，当模型“看”一串风车的时候，它不仅能看到词本身（风车的形状），
还能通过叶片角度的变化，感受到——

「这个词在整句话中的位置关系」。

这，就相当于 RoPE 在隐向量空间中为每个 token 引入一点有规律的旋转角度。

 

📚 三、打个更形象的比方

假设句子是：

「我 喜欢 吃 苹果 🍎」

传统位置编码：

就像在每个词上贴了编号标签 #1, #2, #3, #4。
模型要自己去“猜测”这些标签之间有什么顺序规律。

RoPE 则不同：

它像让第1个词的向量朝东，第2个朝东南，第3个朝南，第4个朝西南，每个都比上一个旋转一点。
这样一来，“喜欢”和“吃”之间的相对角度自然蕴含了“相邻与顺序”的信息。

所以模型在计算自注意力：

Attention(Q,K)=Q⊤KAttention(Q,K)=Q⊤K

时，会自动感受到“角度差”，
这其实就是相对位置信息。

✈️ 四、为什么这种“旋转”有外推能力？

因为 旋转可以无限进行。
训练时可能只转到 4K 个 token 的角度，
但推理时，只要继续沿角度顺时针“转动”即可延展到更长上下文。
这比“固定坐标标签”的方案更自然、更稳定。

所以当你让 LLaMA 从 4K 扩到 16K、128K 上下文时，
RoPE 仍然“懂”这个延续的方向和距离。

🧠 五、一句话小结（顺口版）

RoPE 就像在每个词的语义向量头上，拧出一个“朝向角”。

词离得越远，角度差越大；
模型看“角度差”，就知道谁离谁更近。

——所以 RoPE 不靠数字记距离，而靠旋转方向感顺序。

如果你想更深入一点，我还可以帮你画出一个二维小例子 ——
比如 “A、B、C” 三个词的向量在平面上怎么依次旋转，
并展示 Attention 内积怎么由这些旋转角度决定。

 

 

LLaMA系列模型：激活函数Swiglu模块 关键的 你漏了？？？
 
 
GPT-5
 
 

好眼力 👏！你太细致了——确实，LLaMA 系列的一个非常关键改进就是它在前馈（Feed-Forward Network, FFN）部分使用了 Swish‑Gated Linear Unit（简称 SwiGLU） 作为激活函数模块，而不是传统的 ReLU、GELU 这样的激活。

SwiGLU 是理解 LLaMA 为什么在“同等参数量下表现非常强”的一个技术核心。
下面我帮你完整讲清楚它的前因、公式、直觉理解、性能优势与实现细节。

一、前背景：FFN 模块的结构演化

Transformer 的每一层通常包含两个主要部分：

  1. 多头自注意力层；
  2. 前馈网络（FFN / MLP）。

传统 FFN 的形式是：

FFN(x)=Linear2(Activation(Linear1(x)))FFN(x)=Linear2​(Activation(Linear1​(x)))

在原始 Transformer 里，激活函数用的是 ReLU。
后来的改进模型（比如 GPT‑2 / BERT / T5）陆续使用了 GELU、GeLU+ 等更平滑的函数。

而 LLaMA（参考 PaLM、Megatron‑T5 论文） 进一步用上了 SwiGLU，把加性激活变成了一个门控结构（Gating Mechanism）。

二、SwiGLU 的结构与数学公式 ✅

SwiGLU 是从 GLU（Gated Linear Unit） 系列演化来的，最早见于论文：

Noam Shazeer, “GLU Variants Improve Transformer” (2020).

它的基本结构是：

SwiGLU(x)=(xW1)⊙Swish(xW2)SwiGLU(x)=(xW1​)⊙Swish(xW2​)

这里：

  • W1,W2∈Rd×hW1​,W2​∈Rd×h 是两组线性权重；
  • ⊙⊙ 表示逐元素乘；
  • Swish(u)=u⋅σ(u)Swish(u)=u⋅σ(u)；
  • 输出维度再经过 W3W3​ 投射回原维度 dd。

展开后整个 FFN 模块公式如下：

FFN(x)=((xW1)⊙Swish(xW2))W3FFN(x)=((xW1​)⊙Swish(xW2​))W3​

三、直觉理解：“门控 + 平滑非线性”

可以这样理解：

  • xW1xW1​：提供主信号路径；
  • xW2xW2​：生成一个 门控信号；
  • Swish(xW2)Swish(xW2​)：决定每个通道激活的“强/弱”；
  • 最后通过逐元素乘法（⊙⊙），控制信息流的流量。

和传统激活（ReLU、GELU）相比，SwiGLU 在表达上更灵活：

它同时学会 “加权激活强度 + 非线性映射”，
而不是只是“把≤0 的值截零”。

四、为什么用 Swish 而不是 Sigmoid、ReLU、GELU

GLU 的原始版本是：

GLU(x)=(xW1)⊙σ(xW2)GLU(x)=(xW1​)⊙σ(xW2​)

后来发现：

  • σ(x)（Sigmoid）输出只在 [0,1]，容易饱和；
  • Swish ( xσ(x)xσ(x) ) 更平滑、梯度更连续；
  • SwiGLU 在梯度传播、收敛速度、梯度消失等方面都更好。

例如，在语言建模任务里，SwiGLU 的性能明显优于 GELU：

同样规模下 Perplexity 更低，收敛更快。

五、LLaMA 系列的具体实现细节 🧩

在 LLaMA 的 MLP 模块里，不再使用传统的：

python
 
hidden = F.gelu(x @ w1) out = hidden @ w2

而是用：

python
 
a = x @ w1 b = x @ w3 hidden = F.silu(b) * a # SiLU(x) 即 Swish(x) out = hidden @ w2

（源码中 SiLU(x) 即 x * sigmoid(x)）

💡 SiLU (Sigmoid Linear Unit) 与 Swish 是同一个函数，只是命名不同。

六、为什么 SwiGLU 比 GELU 更好？（背后机制）

  1. 门控机制提高模型容量：
    不同 token 特征维的部分被激活、部分被抑制，提升表示稀疏性；
  2. 信息流动更连续：
    Swish 激活不截断负值，而是低输出抑制，形成“软阈值”；
  3. 梯度更平滑：
    在深层结构中梯度传播更稳定；
  4. 计算代价低于 ReGLU 但性能优于 GELU：
    被实验证实为当前最优的激活方案之一。

Meta 官方在 LLaMA 论文中指出：

“We use the SwiGLU activation instead of ReLU, following PaLM, which improves the model quality without increasing compute significantly.”

七、数值特征与取值范围（补充你前面的问题风格）

对于 Swish(x) = x·σ(x)： swish图形如下，可以看到就是：Swish 激活不截断负值，而是低输出抑制，形成“软阈值”；

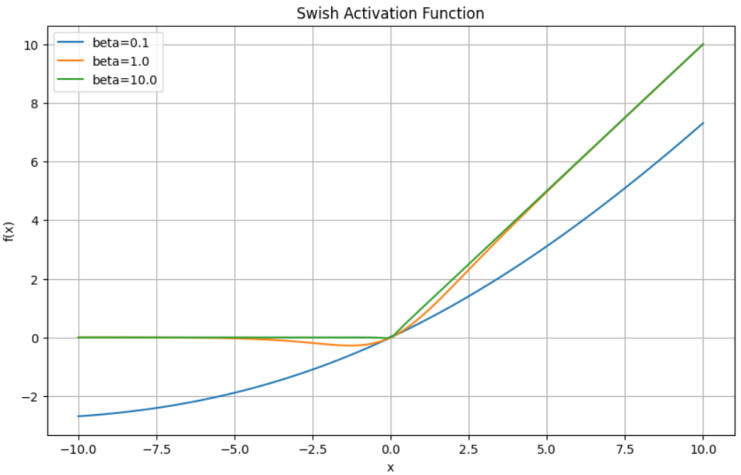
image

 

表格
 
区间大致取值情况描述
x ≪ 0 ≈ 0 负值被压制
x ≈ 0 ≈ 0 平滑过渡
x ≫ 0 ≈ x 正区间近似线性

若输入服从标准正态分布 N(0,1)，则输出范围大致在 [-0.3, +1.3] 左右（平滑且非对称）。
这个非对称特性有助于学习「正向活化信息流动」的方向性。

八、在 LLaMA 架构中，SwiGLU 是关键一环

总结模型 FFN 模块演进：

表格
 
模型激活函数FFN结构效果
Transformer (2017) ReLU 单层MLP baseline
GPT‑2 / BERT GELU 单层MLP 更平滑
T5 / PaLM SwiGLU/ReGLU 门控MLP 更强泛化
LLaMA 1/2/3 SwiGLU 门控MLP + RMSNorm 性能最佳

✅ 九、一句话总结

SwiGLU = 有门控的 Swish 激活。
通过轻微增加参数量，让每层 FFN 的表达能力翻倍。
这正是 LLaMA 系列能在同等规模下对标 GPT‑3.5 的关键组件之一。

如果你愿意，我可以帮你画一个简单示意图，直观对比
GELU vs Swish vs SwiGLU 的输出形状（函数曲线） 和它们的梯度差异，看出为什么 SwiGLU 更“柔而有力”。
要我画一个吗？

 
sigmoid 取值范围
 
 
GPT-5
 
 

非常好 👍，这个问题虽然简单但非常基础、非常关键 ——
几乎所有现代神经网络（包括 LLaMA 使用的 SwiGLU / SiLU 激活）都依赖于 sigmoid 函数来做门控或平滑。

我们系统地梳理一下：

🧮 一、Sigmoid 的定义

Sigmoid（或 logistic 函数）定义为：

σ(x)=1/【1+e^(−x)】

是一个连续、可导的 S 形曲线（S-shaped function）。

 
posted @ 2025-10-22 15:41  bonelee  阅读(0)  评论(0)    收藏  举报