01.强化学习概述
众所周知,机器学习也好深度学习也好,其解决的主要是四类问题:
-
分类问题
-
回归问题
-
聚类问题
-
前两个是有标签的监督学习,后两个是没有标签的非监督学习,这也是数据挖掘领域常需要解决的四个问题。
强化学习是介于监督学习和非监督学习中的另一种学习方式,它可以理解为模拟大自然中生物进化的一个过程,可以理解为,一个生物接收环境给予的状态和奖励,之后做出来下一步的行动,然后环境再给予下一步新的状态和奖励,然后再做出新的动作,如此循环往复
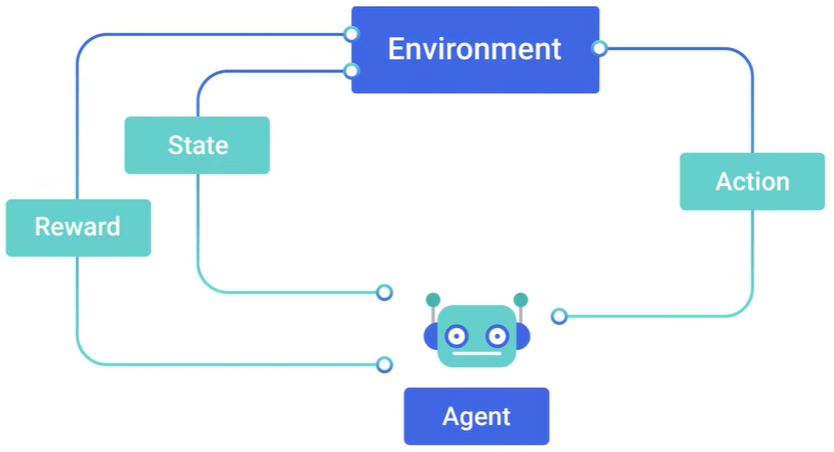
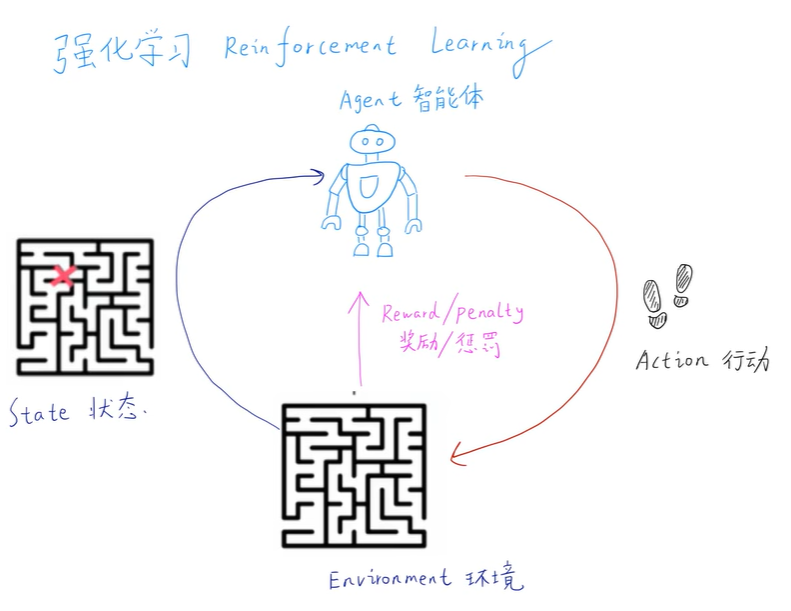
强化学习可以很简单的描述出来,当前的状态s_0,当前的动作a_0,当前的奖励r_1,然后是下一个时刻的状态、动作、奖励,如此循环往复到最终的状态s_n。可以立即为一个马尔可夫过程,即下一刻的状态只与当前的状态有关,而与之前更久远的过去没有关系。
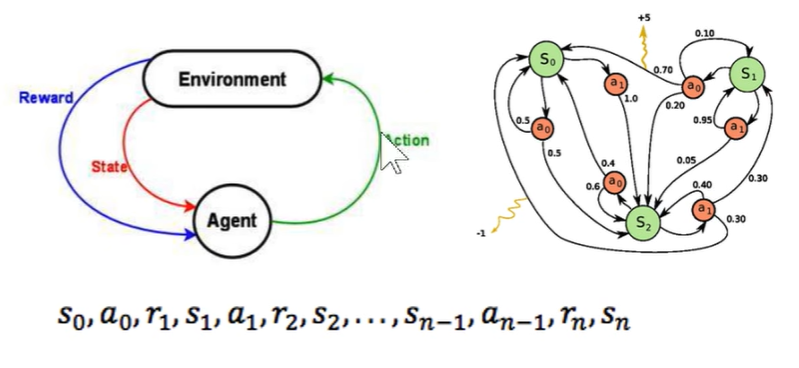
强化学习需要优化的函数,我们把所有的r都进行相加得到R,就好比人的一生活了多久,每一时刻的幸福度都进行相加。但我们想要让这个人,在以后的岁月中都幸福,所以有了R_t的公式,是把t时候之后的所有r进行相加。但是由于我们想要更加珍惜当下于是把t时刻之后的每一个幸福度都加上一个折扣指数γ,越是久远的未来,γ的阶数越高。最后再对此公式进行改写一下,就得到了最后一个公式。于是我们的目标就是R_t最大化。
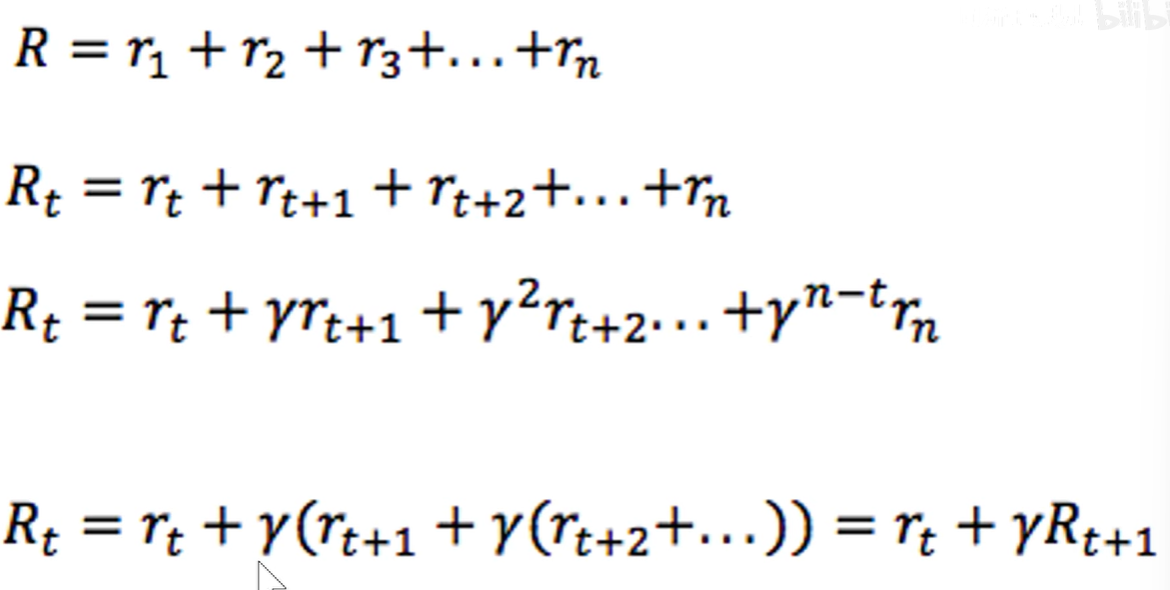
强化学习分类
可以简单地分为两类:不理解环境的Model-Free RL和理解环境的Model-Based RL
-
不理解环境:环境给了什么就是什么。方法:Q-learning、Sarsa、Policy Gradients
-
理解环境:学会了一种模型来代表环境。方法和不理解环境的RL一样,但是多出了一个代表环境的虚拟模型
Model-Free的方法只能一步一步等着真实环境给出的反馈之后才能进入下一步行动。Model-Based的方法是可以通过想象也就是建模来预判断接下来发生的所有情况,然后根据这些想想中的情况来选择最好的那种,并根据这种情况来采取下一步的在真实环境中要做的策略
强化学习也可以分为:基于概率的Policy-Based PL和基于价值的Value-Based RL
-
基于概率的方法,是强化学习中最直接的一种,它能通过感官分析所处环境,直接输出下一步各种行动的概率,然后根据概率采取行动,每一种动作都可能被选中,只是可能性不同,即使某个动作的概率最高还是不一定会选择这个动作。方法:Policy Gradients
-
基于价值的方法,输出的就是所有动作的价值,会根据最高价值来选择动作,相较于基于概率的方法,基于价值的方法更为铁定,只会选择价值最高的动作。方法:Q-learning、Sarsa
然而上述的动作都是不连续的动作,如果是连读的动作,基于价值的方法将会是无能为力的,基于概率的方法将会是通过一个连续的概率分布(就是函数分布的图像,想一下正态分布的图像)在连续的动作中选择特定的动作。如果基于上面的两种方法Policy Grandient和Q-learning能创造出更厉害的一种方法:Actor-Critic,Actor会根据概率做出动作,Critic会根据做出的动作给出对应的价值
还可以分为回合更新(Monte-Carlo update)和单步更新(Temporal-Difference update)
-
回合更新是游戏开始后,我们要等待游戏结束,再总结这个游戏中所有的转折点,再更新我们的行为准则。方法:基础版Policy Grandient、Monte-Carlo Learning
-
单步更新是在游戏中的每一步都在更新,不用等待游戏的结束 。方法:Q-learning、Sarsa、升级版Policy Grandient
最后还能分为在线学习(On-Policy)和离线学习(Off-Policy)
-
在线学习是一定是本人在场,并且是本人在边玩边学习。方法:Sarsa、Sarsa(λ)
-
离线学习是可以选择自己玩,也可以选择看着别人玩,通过看着别人玩,来学习别人的行为准则。方法:Q-learning、Deep Q Network
Q-learning
假设现在有六个房间(5号房间是外面),六个房间并不是所有都互通,我们规定一个奖励,只要是到了外面(5号房间)就可以获得100的奖励(此奖励包括再无号房间停留)
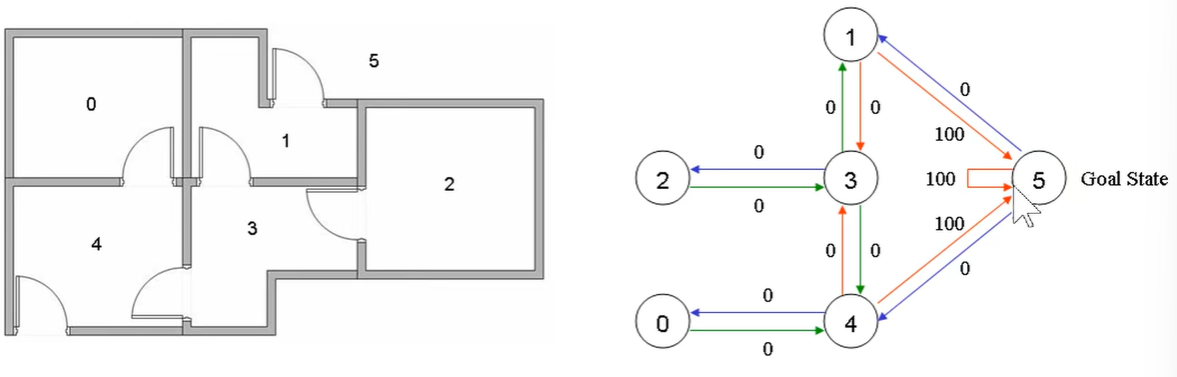
于是我们可以构建一个奖励表,也就是一个矩阵,矩阵的行表示要去的房间(动作action),矩阵的列表示已经在的房间(状态state)其中-1表示不能到达的地方,0表示未能到达外面所以奖励为0,100表示到了外面所以奖励为100。

Q值是当前状态采取某个动作,最大的人生未来幸福度(未来的每一步都采取最优策略形况下的累计奖励)。
找到当前状态下使得Q值最大的动作,作为最佳策略。
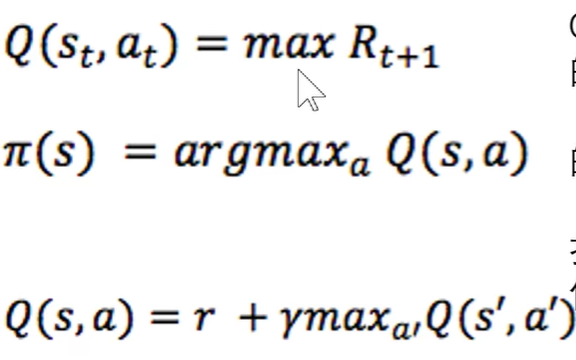
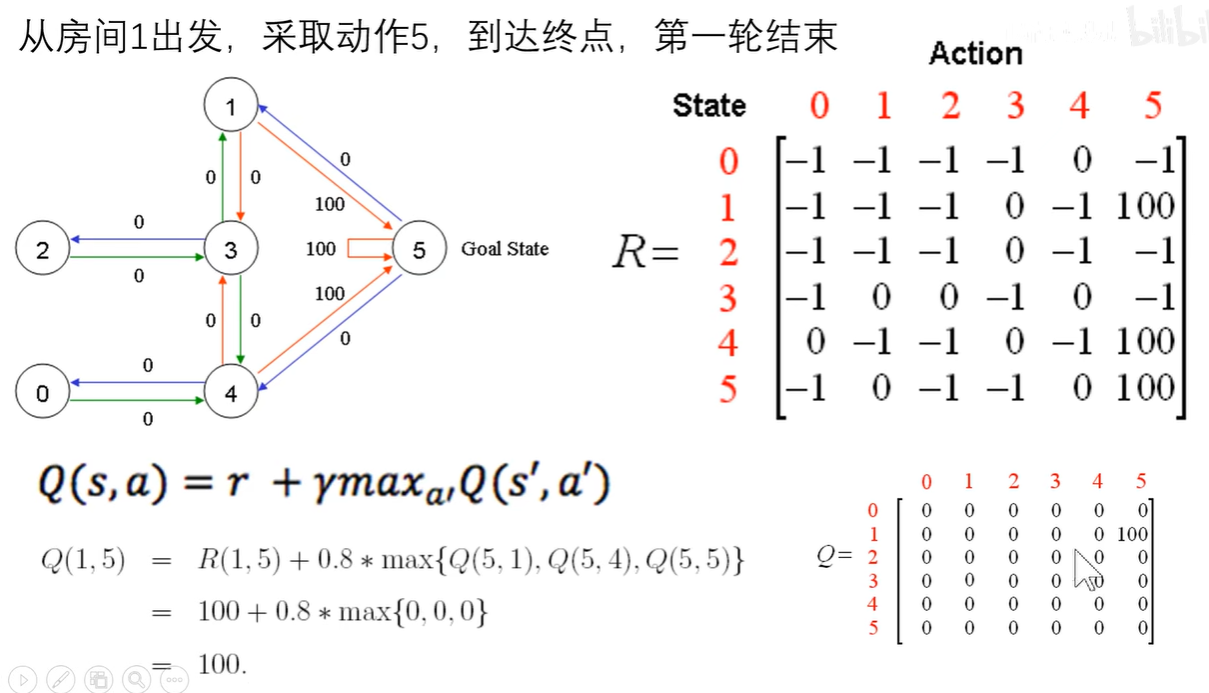
来计算Q值并迭代更新的过程就是Q-learning
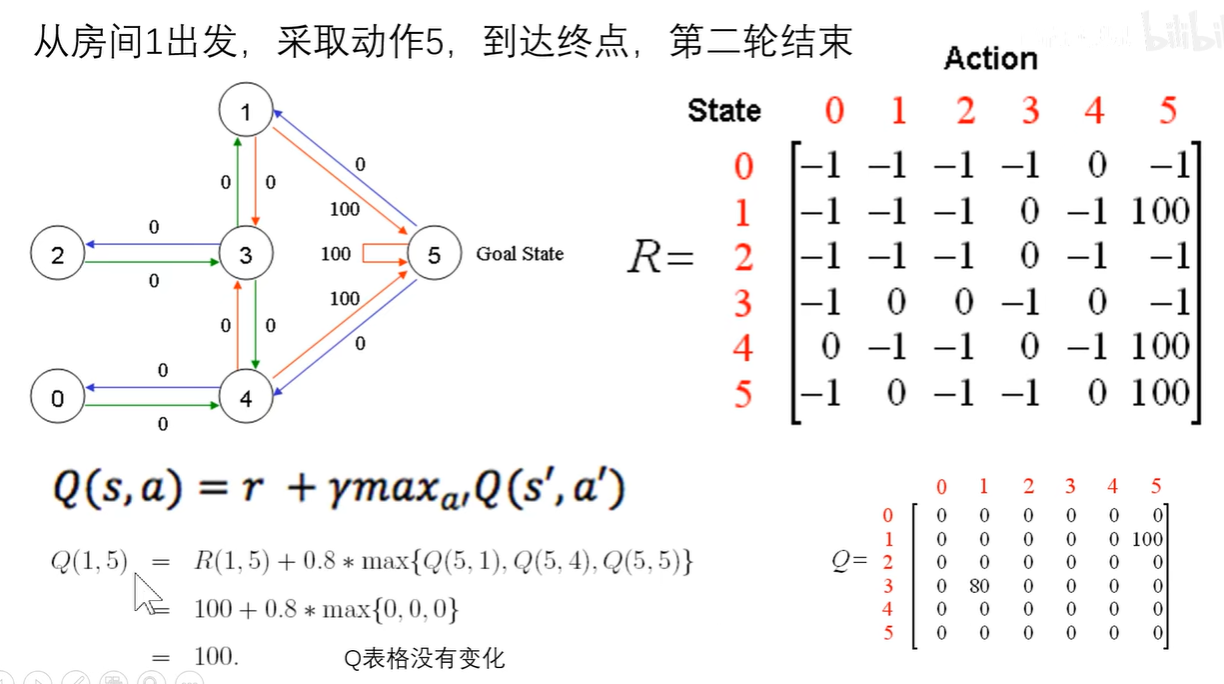
从房间1出发到达5之后获得的奖励R(1,5)是100,再经过计算后得到Q(1,5)是100。
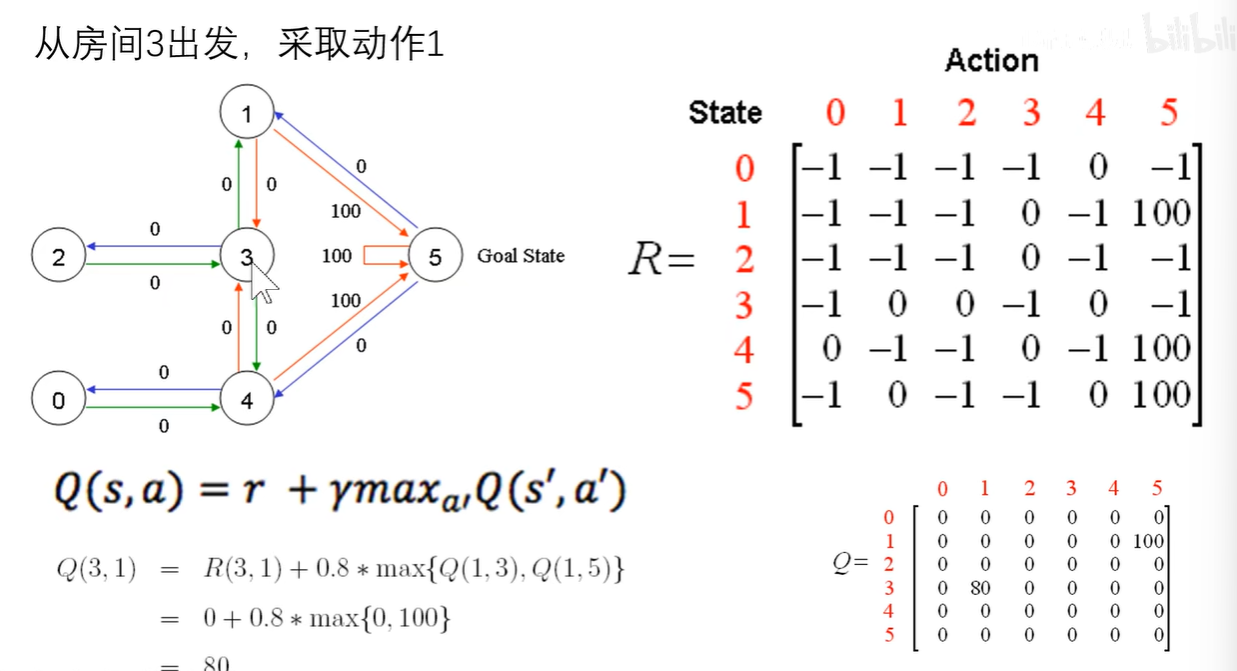
第二轮随机初始化假设从3出发,采取动作1,同样可以计算得到Q(3,1)是80。
第二轮的游戏到达1房间之后并没有结束,假设我们又随机选取到了5,再次根据同样的方式继续更新,我们可以得到Q(1,5)依然是100,并没更新,此时由于已经到达了终点5,于是第二轮结束。
由此过程经过若干轮之后,Q表则会收敛到一个特定的状态
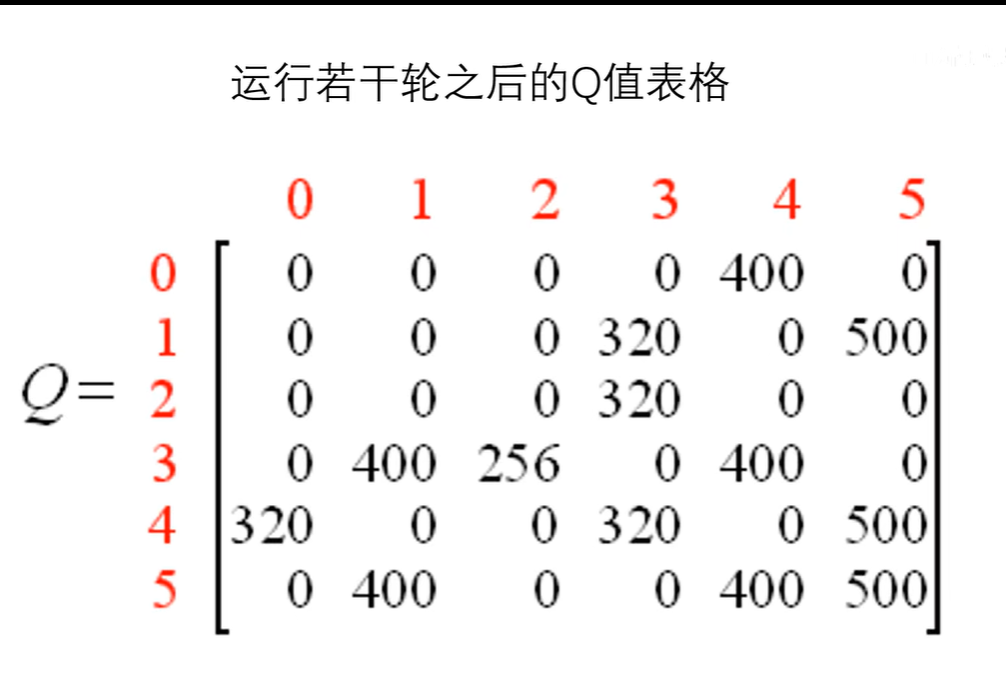
其中值的表示,假设从3房间走到1号房间的Q,即使从1号放假再进行各种选择,其未来的奖励上线也就是400。我们只需要每一步都选择Q值最大的步骤,就可以形成最佳策略
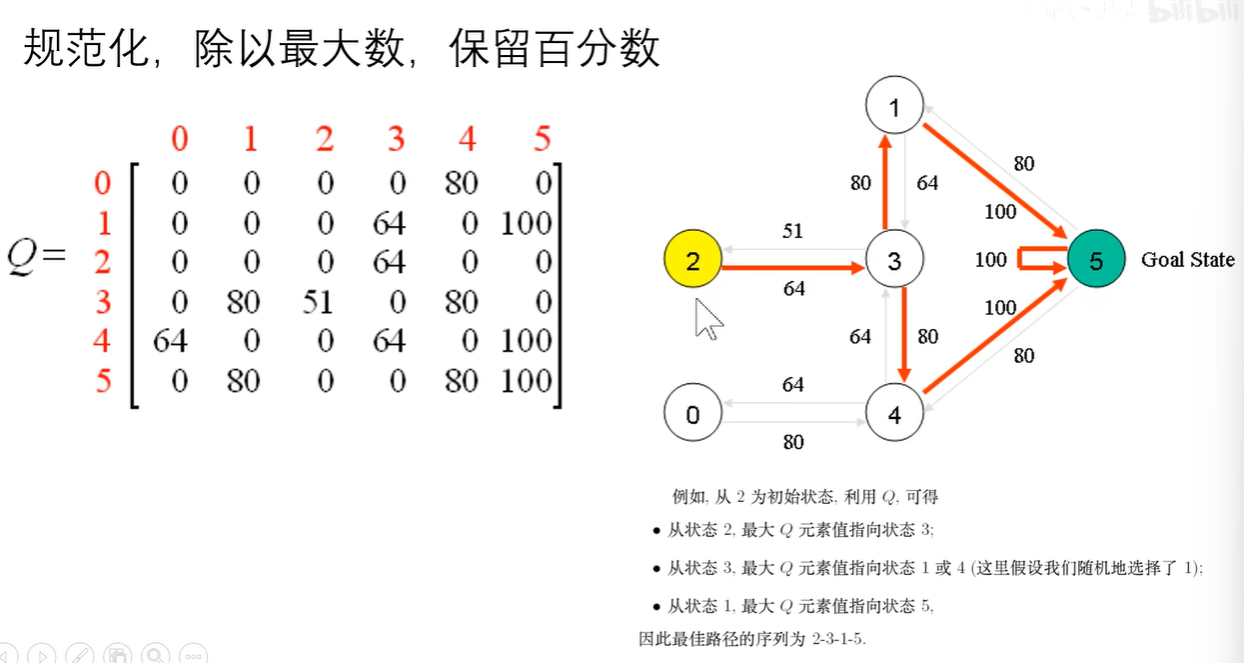
再除以5,进行归一化,得到一个新的更加规范的表格
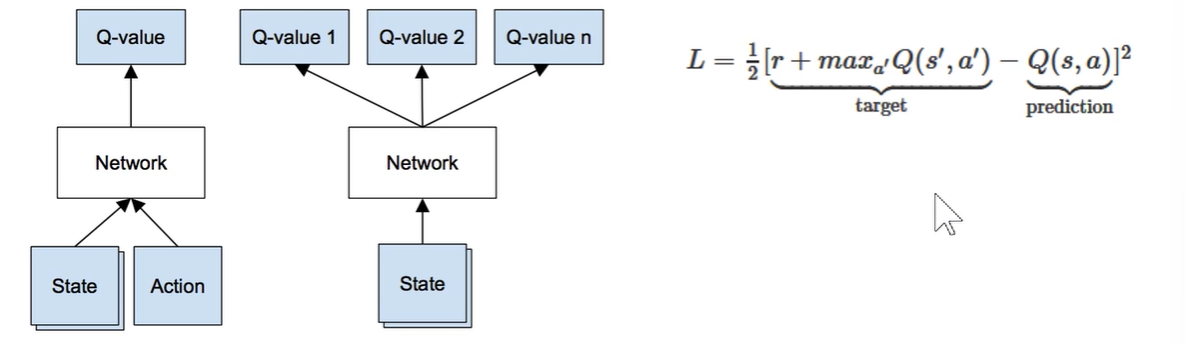
引入深度学习之后的,Loss函数是用已经有标签的target和预估的一个Q值来做差再平方构建Loss函数,将误差最小化
如果上面举例没有听懂,那么就看一个新的例子
假设我们现在机器已经学习好了行为准则,我们现在正处于状态正在写作业s1,我有两个行为a1和a2分别是看电视和写作业,根据已经学习好的数据我们可以知道a2写作业带来的潜在奖励比a1看电视要更高,潜在奖励,我们可以用右边的有关s和a的一个Q表所代替。由表可知,a2带来的潜在奖励是要比a1多,所以我们选择a2动作,于是我们的状态就会更新为s2

当状态更新为s2之后,我们依然是还有两个选择,并重复上面的过程,我们会选择Q(s2,a2)即Q值较大的那一个。

到此我们就知道Q-learning是根据什么样的行为准则进行决策的,那么就要研究一下Q表是如何进行更新的
依然是上面的的例子,我们知道s1的状态下,根据Q表需要进行动作a2,于是我们到达了s2的状态,于是要更新Q表,但是我们并没有在实例中采取任何行动,由于并不知道应该去选择哪个动作,我们也没与去选择动作。shih于是我们想想自己在s2上采取的每种行动,分别看看两种行为哪个Q值更大

假设Q(s2,a2)的值比Q(s2,a1)的值要更大,所以我们把一个大的Q(s2)的值乘上一个衰减值γ,并加上到达s2时所获得的奖励R,由于我们会获取实实在在的奖励R,于是我们把这个作为现实中的Q(s1,a2)的值,但是我们之前根据Q表已经估计过了Q(s1,a2)的值,于是有了现实值和估计值,我们就能更新Q(s1,a2),根据估计与现实的差距,将这个差距乘以一个学习效率α再加上老的Q(s1,a2)变成更新后的值。
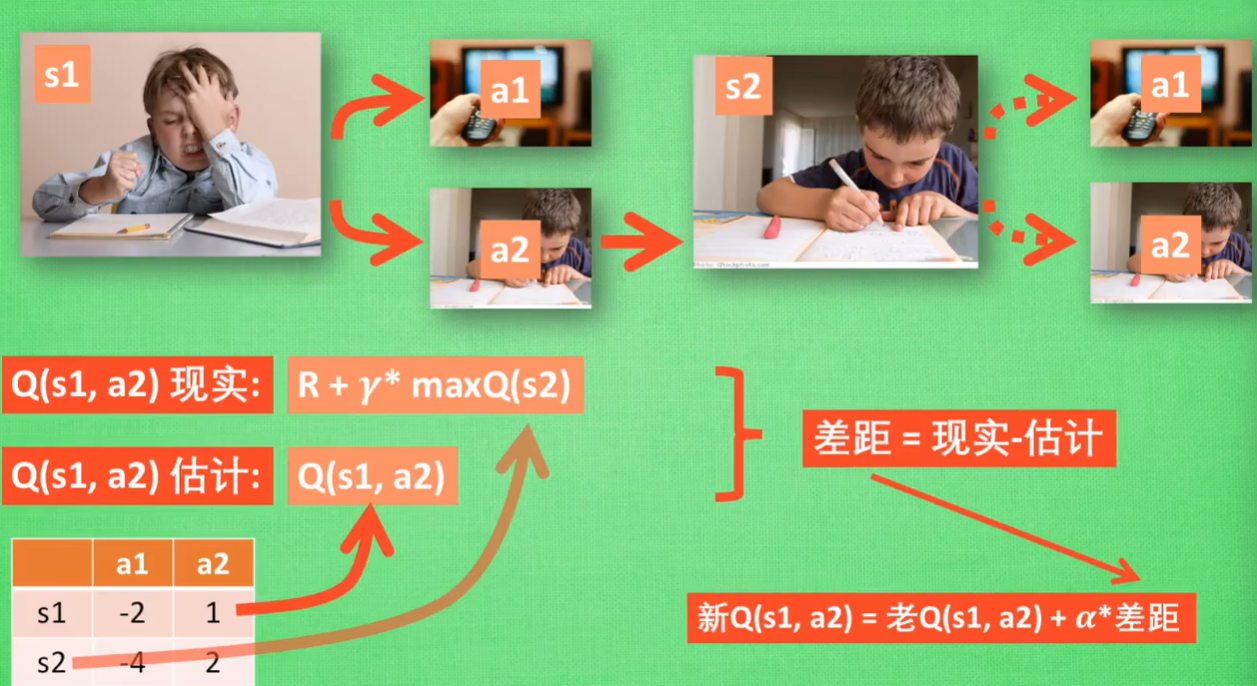
虽然我们用maxQ(s2)来估计下一个s2的状态,但还没有在状态s2做出任何的行为,s2的决策部分,要等到更新Q表之后再重新另外做。
其中的三个重要参数:
-
ε表示用在决策上的一种策略,比如当ε=0.9时,就说明有90%的情况我们会根据Q表的最优值来选择行为,另外10%的情况是随机选择行为。
-
α是学习效率,来决定这一次误差有多少要被学习
-
γ是对未来奖励的衰减值

当把Q(s1)写开之后可以发现,其值和未来所有奖励都有关系,但是距离s1越远的奖励衰减越严重




 浙公网安备 33010602011771号
浙公网安备 33010602011771号