新经济地理学核心边缘模型（CP）数值模拟——（一）

新经济地理学核心边缘模型（CP）数值模拟

首先摆上《空间经济学》书中的瞬时均衡方程组：

\[\begin{align} Y_1 &=\mu\lambda w_1+\frac{1-\mu}{2} \\ Y_2 &=\mu(1-\lambda) w_2+\frac{1-\mu}{2} \\ G_1 &=[\lambda w_1^{1-\sigma}+(1-\lambda)(w_2T)^{1-\sigma}]^{1/(1-\sigma)} \\ G_2 &=[\lambda (w_1T)^{1-\sigma}+(1-\lambda)w_2^{1-\sigma}]^{1/(1-\sigma)} \\ w_1 &=[Y_1G_1^{\sigma-1}+Y_2G_2^{\sigma-1}T^{1-\sigma}]^{1/\sigma} \\ w_2 &=[Y_1G_1^{\sigma-1}T^{1-\sigma}+Y_2G_2^{\sigma-1}]^{1/\sigma} \\ \omega_1 &=w_1G^{-\mu} \\ \omega_2 &=w_2G^{-\mu} \end{align} \]

该模型是一个非线性方程组，用matlab自带的 fsolve 函数就可以求数值解。但是求数值解的一个关键问题是选择初始值，选的不好会导致不好的计算结果。这个模型咋一看有8个变量，如果一个个去筛选初始值就太麻烦了。

在安虎森教授的《新经济地理学原理》中，安教授是用EXCEL做的数值模拟，他把模型转换成只需要关注\(w_1、w_2\)两个变量的方程组，一次次输入初始值，选出比较好估计值。（实在是）

其实这里我们仔细观察上面的方程组就会发现，前六个方程可以自成一个独立的联立方程组，而前四个方程的右边都只有 \(w_1、w_2\) 两个变量，因此可以把前四个方程带入式(5)、式(6)，得到只有 \(w_1、w_2\) 如的下方程组：

\[\begin{align} w_1^{\sigma}=\frac{\mu\lambda w_1+\frac{1-\mu}{2}}{\lambda w_1^{1-\sigma}+(1-\lambda)(w_2T)^{1-\sigma}}+\frac{[\mu(1-\lambda)w_2+\frac{1-\mu}{2}]T^{1-\sigma}}{\lambda(w_1T)^{1-\sigma}+(1-\lambda)w_2^{1-\sigma}}\\ w_2^{\sigma}=\frac{(\mu\lambda w_1+\frac{1-\mu}{2})T^{1-\sigma}}{\lambda w_1^{1-\sigma}+(1-\lambda)(w_2T)^{1-\sigma}}+\frac{\mu(1-\lambda)w_2+\frac{1-\mu}{2}}{\lambda(w_1T)^{1-\sigma}+(1-\lambda)w_2^{1-\sigma}}\\ \end{align} \]

这样，我们就可以只需要考虑两个变量了。

下面直接上matlab代码：

clear
clc

Mu=0.4;
Sigma=5;
Lambda=(1:999)*0.001;
A=[];
B=[];
C=[];


T=1.5;
for i=1:999
    f= @(x) [x(1)^Sigma - (Mu*Lambda(i)*x(1)+(1-Mu)/2)/(Lambda(i)*x(1)^(1-Sigma)+(1-Lambda(i))*(x(2)*T)^(1-Sigma)) - (Mu*(1-Lambda(i))*x(2)+(1-Mu)/2)*T^(1-Sigma)/(Lambda(i)*(x(1)*T)^(1-Sigma)+(1-Lambda(i))*x(2)^(1-Sigma));   
             x(2)^Sigma - (Mu*Lambda(i)*x(1)+(1-Mu)/2)*T^(1-Sigma)/(Lambda(i)*x(1)^(1-Sigma)+(1-Lambda(i))*(x(2)*T)^(1-Sigma)) - (Mu*(1-Lambda(i))*x(2)+(1-Mu)/2)/(Lambda(i)*(x(1)*T)^(1-Sigma)+(1-Lambda(i))*x(2)^(1-Sigma))];
    
    X0=[1,1];
    X=fsolve(f,X0);
    G1=(Lambda(i)*X(1)^(1-Sigma)+(1-Lambda(i))*(X(2)*T)^(1-Sigma))^(1/(1-Sigma));
    G2=(Lambda(i)*(X(1)*T)^(1-Sigma)+(1-Lambda(i))*X(2)^(1-Sigma))^(1/(1-Sigma));
    w1=X(1)*G1^(-Mu);
    w2=X(2)*G2^(-Mu);
    A(i)=w1-w2;
    
end

T=1.7;
for i=1:999
    f= @(x) [x(1)^Sigma - (Mu*Lambda(i)*x(1)+(1-Mu)/2)/(Lambda(i)*x(1)^(1-Sigma)+(1-Lambda(i))*(x(2)*T)^(1-Sigma)) - (Mu*(1-Lambda(i))*x(2)+(1-Mu)/2)*T^(1-Sigma)/(Lambda(i)*(x(1)*T)^(1-Sigma)+(1-Lambda(i))*x(2)^(1-Sigma));   
             x(2)^Sigma - (Mu*Lambda(i)*x(1)+(1-Mu)/2)*T^(1-Sigma)/(Lambda(i)*x(1)^(1-Sigma)+(1-Lambda(i))*(x(2)*T)^(1-Sigma)) - (Mu*(1-Lambda(i))*x(2)+(1-Mu)/2)/(Lambda(i)*(x(1)*T)^(1-Sigma)+(1-Lambda(i))*x(2)^(1-Sigma))];
    
    X0=[1,1];
    X=fsolve(f,X0);
    G1=(Lambda(i)*X(1)^(1-Sigma)+(1-Lambda(i))*(X(2)*T)^(1-Sigma))^(1/(1-Sigma));
    G2=(Lambda(i)*(X(1)*T)^(1-Sigma)+(1-Lambda(i))*X(2)^(1-Sigma))^(1/(1-Sigma));
    w1=X(1)*G1^(-Mu);
    w2=X(2)*G2^(-Mu);
    B(i)=w1-w2;
    
end

T=2.1;
for i=1:500
    f= @(x) [x(1)^Sigma - (Mu*Lambda(i)*x(1)+(1-Mu)/2)/(Lambda(i)*x(1)^(1-Sigma)+(1-Lambda(i))*(x(2)*T)^(1-Sigma)) - (Mu*(1-Lambda(i))*x(2)+(1-Mu)/2)*T^(1-Sigma)/(Lambda(i)*(x(1)*T)^(1-Sigma)+(1-Lambda(i))*x(2)^(1-Sigma));   
             x(2)^Sigma - (Mu*Lambda(i)*x(1)+(1-Mu)/2)*T^(1-Sigma)/(Lambda(i)*x(1)^(1-Sigma)+(1-Lambda(i))*(x(2)*T)^(1-Sigma)) - (Mu*(1-Lambda(i))*x(2)+(1-Mu)/2)/(Lambda(i)*(x(1)*T)^(1-Sigma)+(1-Lambda(i))*x(2)^(1-Sigma))];
    
    X0=[1.2,0.98];
    X=fsolve(f,X0);
    G1=(Lambda(i)*X(1)^(1-Sigma)+(1-Lambda(i))*(X(2)*T)^(1-Sigma))^(1/(1-Sigma));
    G2=(Lambda(i)*(X(1)*T)^(1-Sigma)+(1-Lambda(i))*X(2)^(1-Sigma))^(1/(1-Sigma));
    w1=X(1)*G1^(-Mu);
    w2=X(2)*G2^(-Mu);
    C(i)=w1-w2;
    
end
for i=501:999
    f= @(x) [x(1)^Sigma - (Mu*Lambda(i)*x(1)+(1-Mu)/2)/(Lambda(i)*x(1)^(1-Sigma)+(1-Lambda(i))*(x(2)*T)^(1-Sigma)) - (Mu*(1-Lambda(i))*x(2)+(1-Mu)/2)*T^(1-Sigma)/(Lambda(i)*(x(1)*T)^(1-Sigma)+(1-Lambda(i))*x(2)^(1-Sigma));   
             x(2)^Sigma - (Mu*Lambda(i)*x(1)+(1-Mu)/2)*T^(1-Sigma)/(Lambda(i)*x(1)^(1-Sigma)+(1-Lambda(i))*(x(2)*T)^(1-Sigma)) - (Mu*(1-Lambda(i))*x(2)+(1-Mu)/2)/(Lambda(i)*(x(1)*T)^(1-Sigma)+(1-Lambda(i))*x(2)^(1-Sigma))];
    
    X0=[0.98,1.2];
    X=fsolve(f,X0);
    G1=(Lambda(i)*X(1)^(1-Sigma)+(1-Lambda(i))*(X(2)*T)^(1-Sigma))^(1/(1-Sigma));
    G2=(Lambda(i)*(X(1)*T)^(1-Sigma)+(1-Lambda(i))*X(2)^(1-Sigma))^(1/(1-Sigma));
    w1=X(1)*G1^(-Mu);
    w2=X(2)*G2^(-Mu);
    C(i)=w1-w2;
    
end

plot(Lambda,A)
plot(Lambda,B)
plot(Lambda,C)

注意到在T=2.1的时候，我把循环拆成了两个部分。这是因为在T=2.1的时候输入初始值X0=[1,1]d得不到收敛的结果，模拟结果如下:

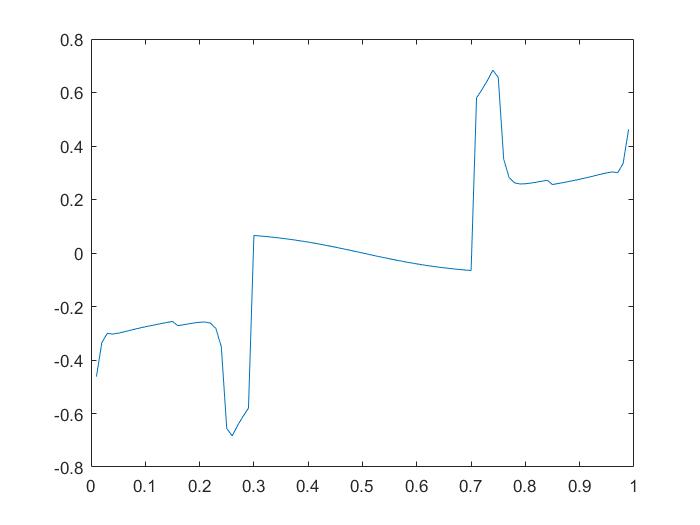
哈哈哈，😓 。可以看到，在中间的时候数值模拟结果还是收敛的，到了两端就不行。于是我用安教授的方法在EXCEL上快速测试出了一对还算可以的数值 1.2和0.98 ，即 X0=[1.2,0.98] 和 X0=[0.98,1.2] 。然后把T=2.1情况下的循环拆成两部分，分别处理，最终的得到了满意的结果。如下所示：

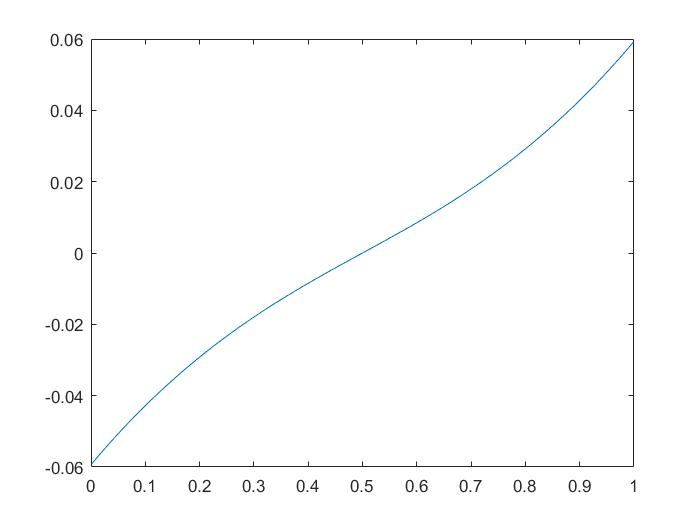
\(图(1):\mu=0.4 ,\sigma=5 ,T=1.5\)

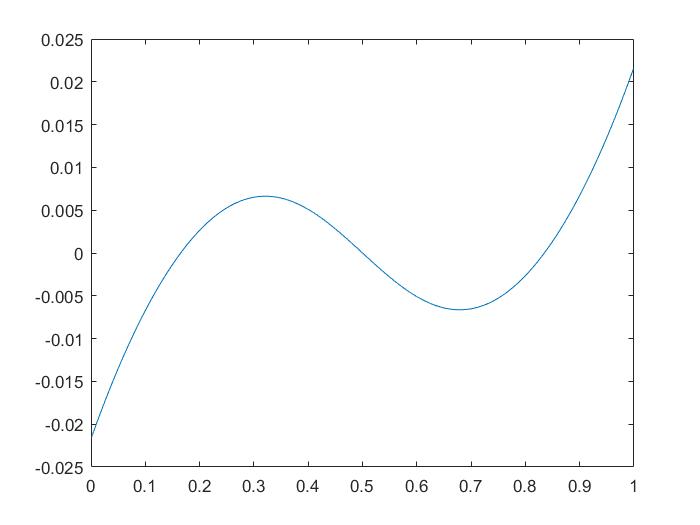
\(图(2): \mu=0.4 ,\sigma=5 ,T=1.7\)

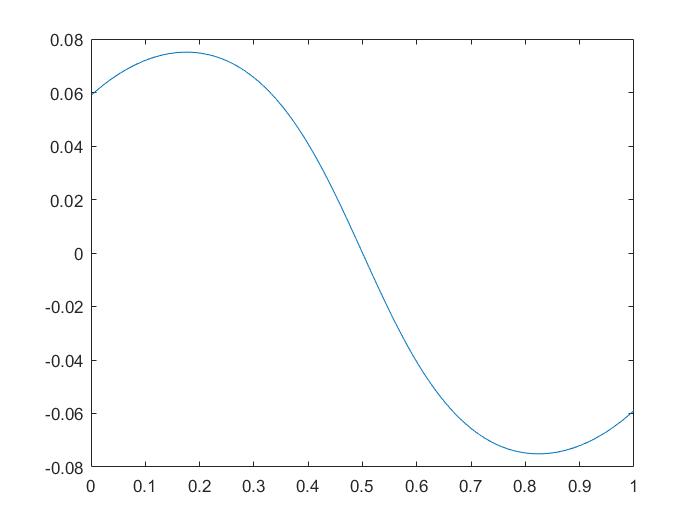
\(图(3):\mu=0.4 ,\sigma=5 ,T=1.5\)

和《空间经济学》书中展示的一模一样了！！！😁