从几何角度理解单纯形法（Simple algorithm)

标准型

\[\begin{split} &\min\quad &&c^Tx\\ &s.t.&Ax&\leq b \\ & &x &\geq 0 \end{split} \]

​ 假设A是一个行满秩的矩阵，否则通过一些变化可以使A变成行满秩

如果将一个一般化的线性规划问题化成一个标准型？

​ 如果在原始的线性规划问题中，有的变量不是非负的（自由变量），那么我们可以用两个非负的变量替代它，即

\[\begin{split} x_i = x_i'-x_i''\\ x_i',x_i'' \ge 0 \end{split} \]

​ 如果有的约束条件是等式，则可以等价地用两个不等式进行表示，即

\[\sum_{i=1}^n a_{ji}x_i = b\quad\Rightarrow \quad\sum_{i=1}^n a_{ji}x_i \ge b , \sum_{i=1}^n a_{ji}x_i \le b \]

​ 如果有的约束形如 \(\sum_{i=1}^n a_{ji}x_i \ge b\)，在不等式两边同时取负号即可

松弛型

\[\begin{split} &\min\quad &&c^Tx\\ &s.t.&Ax&= b \\ & &x &\geq 0 \end{split} \]

​ 可以在标准型的基础上加入一些松弛变量从而转化为松弛型。

单纯形法

​ 现在针对标准型，考虑单纯形法，可以看出相较于线性方程组，松弛型的线性规划问题多了目标函数和变量的非负约束。

变量非负性

​ 变量非负性的约束实质上使得线性方程组的可行域变成了多面体，考虑\(\sum_{i=1}^n a_{ji}x_i = b\) ，因为\(x_1 \ge 0\) ，所以有 \(-\sum_{i=2}^n a_{ji}x_i + b\ge 0\)，即对可行域有了一个线性的约束

目标函数

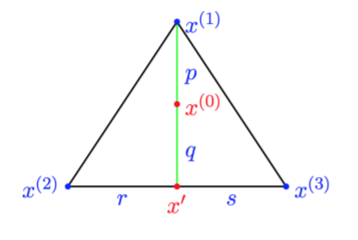
​ 目标函数的存在，使得最优解会在可行域的顶点处产生。所以，不需要考虑可行域的内点，只需要在顶点集合内进行搜索最优解即可。

​ 了解了线性规划问题和线性方程组问题的区别之后，我们将线性规划问题转化成了在一个多面体区域内，找寻最优解对应的那个顶点，看起来好像很简单，但是随着约束数量的增加，顶点个数也是以指数形式不断增加，如何有效地搜索最优解呢？我们可以考虑以下四个问题：

1. 为什么我们最优解一定会在顶点处？
2. 怎么样从线性规划问题中得到它的顶点？
3. 得到顶点后，如何在每一步迭代过程中对目标函数值进行提升？
4. 迭代到什么程度停止？

解决了这四个问题，就得到了一个可以获得线性规划问题解的一个可行算法，那我们一个一个来解决这些问题。

1.为什么我们最优解一定会在顶点处？

​ 这里我们利用反证法，不妨假设最优解在多面体内部，那么这个点一定可以用顶点进行线性表出，那么最优解会有一个顶点分解，即\(c^Tx=\lambda_1 c^Tx_1+\lambda_2 c^Tx_2+\cdots+\lambda_k c^Tx_k，\sum_{i=1}^k \lambda_i=1\)，那么取这些顶点中目标函数值最小的那个顶点即 \(x_j, j = argmin\{\lambda_j c^Tx_j\}\) ，则有\(c^Tx\ge c^Tx_j\)，只有当\(x=x_j\)时，等式成立，与\(x\)是非顶点的最优解矛盾，所以最优解一定会在顶点处。

2.怎么样从线性规划问题中得到它的顶点？

​ 首先，我们会得到一个很直观的认识，即可行域这个多面体的任何一个顶点对应了矩阵A的一组基。

​ 很直观的我们可以知道，可行域的一个顶点x对应了约束条件等号成立下的一组解，不妨记作\((x_1,x_2,\cdots,x_n)^T\)，假设前m个坐标非0，下面证明A中对应的这m个列向量是A的一组基：

​ 还是利用反证法，假设\(x_1,x_2,\cdots,x_m\)线性相关，也即是说，存在一组不全为0的参数\({\lambda_i}\)，使得\(\lambda_1x_1+\lambda_2x_2+\cdots+\lambda_mx_m=0\)，构造一个向量\(\lambda = (\lambda_1,\lambda_2,\cdots,\lambda_m,0,0,\cdots,0)^T\)，可以知道\(A\lambda=0\)。那么对于两个与该顶点共线的点\(x'=x+\theta \lambda\)和\(x'=x-\theta \lambda\)，都有\(Ax'=Ax''=b\) ，即这两个点也都在可行域内，那么就与x是凸多面体的顶点（不能由凸多面体内其他点线性表出）矛盾了。所以这一组线性向量线性无关。

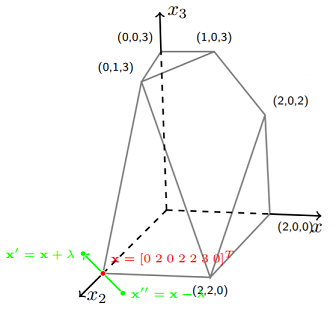
​ 那么为什么说这一组向量就是矩阵A的一组基呢？考虑A的一个子矩阵，A‘，由前m列组成。因为其余项为0，所以有\(Ax=A'x'=b\)，因为矩阵A‘行满秩，所以很自然的可以得出，\(x'=(x_1,x_2,\cdots,x_m)^T\)是A’的一组基，也即是A的一组基。

​ 这样我们就把凸多面体可行域这一具象的概念和矩阵的一组基这一抽象概念建立起了联系，而后者则是利于编程实现的。只要能找到矩阵的一组基，就意味找找到了可行域中的一个顶点。

3.得到顶点后，如何在每一步迭代过程中对目标函数值进行提升？

​ 既然一组基对应了一个顶点，我们知道，可行域会有多个顶点，也即对应了线性规划的矩阵的多组基，怎么从这些基中进行选基呢？

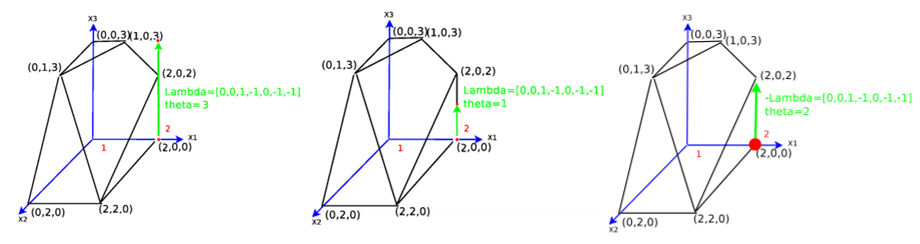
​ 假设\(x’=(x_1,x_2,\cdots,x_m)^T\)对应了A’的一组基，而\(x=(x_1,x_2,\cdots,x_m,0,\cdots,0)^T\)即对应了A的一组基，对应的列向量用\(a_i\)表示，现在我们考虑一个非基变量\(a_k\)，那么它一定可以写成基变量的一个线性组合，不妨写作\(a_k = \lambda_1a_1+\lambda_2a_2+\cdots+\lambda_ma_m\)，现在我们构建一个新的向量\(x_{updata}=x-\theta\lambda\)，其中\(\lambda=(\lambda_1,\lambda_2,\cdots,\lambda_m,0,\cdots,-1,\cdots,0)^T\) ，\(\theta>0\)，看看这个向量相较于原向量有什么变化。

​ 注意到非基向量对应的系数为-1，即在\(x_{updata}\)中，\(a_k\)对应的解变量大于0，基变量中对应系数为负数的解变量仍然大于0，而对应系数为负数的那部分解变量，随着\(\theta\)的增加，肯定会有一个分量先到达0，此时恰好有n个基变量大于0，即对应了新的一组基。从几何上进行理解，是\(a_k\)和之前基向量中的某m-1个基向量组成一组新的基，对应了可行域的另一个定点，而\(\lambda\)则是连接着两个顶点的方向向量。

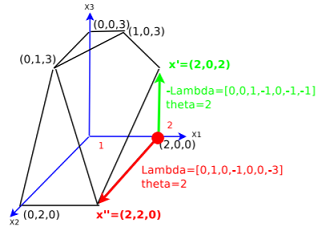
这个时候，系数向量实际是是从可行域的一个顶点指向另一个顶点的。我们可以借助于基变换进行理解，既然\(a_k\)可以写作当前基向量的一个线性组合，那么\(a_k\)必然可以和当前基向量中的某m-1个基向量组成一组新的基\((a_1',a_2',\cdots,a_m')^T\)，对应了可行域的另一个顶点，而此时对应的坐标变换为\(x=x'-\theta\lambda\) ，所以我们知道了如何从一个顶点转移到了另一个顶点，那么我们怎么去选择呢？

​ 从上述过程可以看出，顶点转移过程其实就是基变换的过程，也即是从当前基向量中选择一个出基向量，从非基向量中选择一个进基向量构成一组新的基向量。那么如何选择进基向量和出基向量？

​ 出基变量的选择：

​ 考虑从顶点出发，沿边的方向行进的距离\(\theta\)。取\(\theta=\min_{\lambda_i>0} \frac{x_i}{\lambda_i}\) ，此时出基变量对应解变量值为0，其他基变量大于0，而进基变量对应值大于0，此时得到了一组新的基。如果\(\theta\)过大，\(\theta\gt\min_{\lambda_i>0} \frac{x_i}{\lambda_i}\)，则存在解变量小于0，即当前点不在可行域内；而如果\(\theta\)过小，\(\theta\gt\min_{\lambda_i>0} \frac{x_i}{\lambda_i}\)，则有解变量之间线性相关，并非可行域的一个顶点，所以只能选择\(\theta=\min_{\lambda_i>0} \frac{x_i}{\lambda_i}\)。

​ 进基变量的选择

​ 当从一个顶点转移到另一个顶点时，目标函数的变化值为\(c^Tx_{update}-c^Tx=-\theta c^T\lambda=(c_e-\sum\lambda_ic_i)\theta\) ，因为我们希望目标函数越来越小，即是\((c_e-\sum\lambda_ic_i)\theta\) 尽可能小。此时当前步的转移获得的收益最大。

4.迭代到什么程度停止？

​ 如果当前状态，如果所有的非基向量对应的\((c_e-\sum\lambda_ic_i)\theta\ge 0\)总成立，即不存在一个相邻定点比当前顶点更优，则迭代停止。