笔记——字符串
蓝月の笔记——字符串篇
摘要
一些串串
\(\quad\qquad\)——某yl新高一学长
字串
\(\quad\qquad\)——某yl新高一学长のppt
Warning
本文中字符串的下标有时从 \(1\) 开始有时从 \(0\) 开始,请自行分辨无特殊说明从 \(1\) 开始
字符串长度无特殊说明为 \(n\)
字符串无特殊说明表示为 \(s\)
Part 1 概念
相信读者都知道字符串的概念了,那就只快速过一遍
子序列和子串都是原串的一部分,字串要求连续,子序列只要求保证相对位置即可
前缀是从 \(1\) 开始的子串,后缀是以 \(n\) 结尾的子串,真(前/后)缀为不是本身的(前/后)缀
回文串是满足 \(\forall i \in [1,n],s_i=s_{n-i+1}\),即正反看都一样,如 acbca
Part 2 字典树 Trie
原本读音和 tree 一样,为了区分读作 try
先上图:
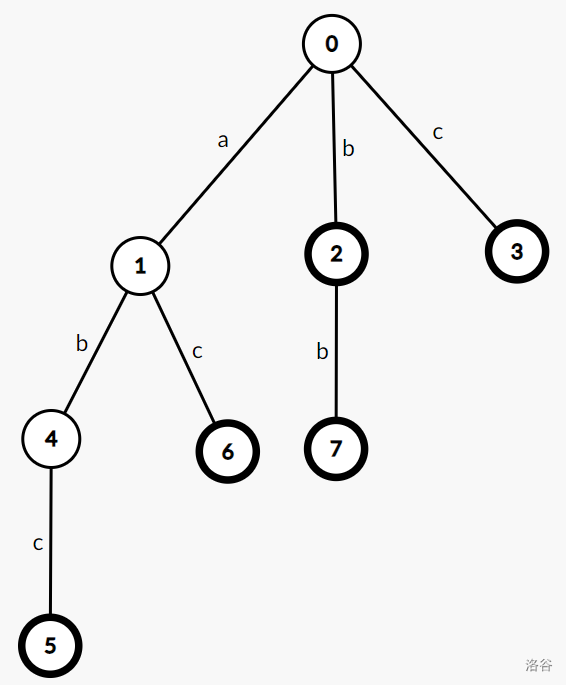
这是一颗存储了字符串 abc,ac,b,bb,c 的字典树
在字典树中,边代表字符,点只是用来连接的。也可以把边和点换过来,只不过根节点不方便存储,不做考虑
可以看到,字典树里从根节点到加粗节点都表示了一个字符串,一条路径上可能有两个字符串
存储方式:可以用 to 数组存储每一个节点通过字符前往的下一个节点,用 ed 数组存储有多少个字符串以这个节点做结尾,即图片中的标粗操作
最坏情况为满 \(26\) 叉数,所以要使用动态开点
下面是 Trie 的模板:
const int kMaxN = 2e5 + 5, kMaxC = 26 + 5; // 默认只有小写字母
struct Trie {
int tot, to[kMaxN][kMaxC], ed[kMaxN];
void Insert(int sz, string s, int u = 0) { // sz为字符串长度
for (int i = 1; i <= sz; i++) {
if (to[u][s[i] - 'a' + 1] == 0) { // 当前节点没有通过当前字符指向的边
to[u][s[i] - 'a' + 1] = ++tot, u = tot; // 动态开点
} else {
u = to[u][s[i] - 'a' + 1]; // 前进到下一个节点
}
}
}
bool Query(int sz, string s, int u = 0) {
for (int i = 1; i <= sz; i++) {
if (to[u][s[i] - 'a' + 1] == 0) { // 当前字符失配了
return 0; // 返回没找到
}
u = to[u][s[i] - 'a' + 1]; // 前进到下一个节点
}
return ed[u]; // 如果没有以最后字符结尾也不算找到
}
};
习题:
Luogu P8306 【模板】字典树 注意可能会出现大写字母和数字,需要转换
TJOI2010 阅读理解 需要开多颗字典树处理
Luogu P2580 于是他错误的点名开始了 开一个数组存储是否被搜索过即可
Ex. 01 Trie
用于存储数字的 Trie
容易想到将数字转换为二进制就同样变成的一个字符串,同样可以用 Trie 储存
注意要从高位向低位存储
代码:
const int kMaxN = 2e5 + 5;
struct Trie {
int tot, to[kMaxN][2], ed[kMaxN];
void Insert(int s, int u = 0) {
for (int i = 31; ~i; i--) { // 默认数字是32位整型(int)
int v = (s >> i) & 1; // 待存数字二进制的第i位
if (to[u][v] == 0) {
to[u][v] = ++tot, u = tot;
} else {
u = to[u][v];
}
}
}
bool Query(int s, int u = 0) {
for (int i = 31; ~i; i--) {
int v = (s >> i) & 1;
if (to[u][v] == 0) {
return 0;
}
u = to[u][v];
}
return ed[u];
}
};
下文中 \(\bigoplus\) 表示异或
钦定根节点为点 \(1\)
由于 \(x \bigoplus x=0\),我们可以得到一个 trick,因为树上两点的路径是两个点到他们的 LCA 的路径拼起来,又因为树上两点到根的路径有且仅有从 LCA 到根的部分是重复的。于是我们定义 \(e_i\) 为点 \(i\) 到根节点的路径的异或和,那么树上任意两点 \(u\) 和 \(v\) 的路径异或和为 \(e_u \bigoplus e_v\)
求出 \(e\) 只需要进行一边 DFS 即可,时间复杂度为 \(O(n)\)。但求出答案需要 \(O(n^2)\) 枚举,所以我们考虑优化这一段
我们将 \(e\) 数组中的每一个值存入 01 Trie 中由于从高位向低位储存的性质,对于每一个节点的每一位尽量走这一位不同的方向,如果没有就只能向下走了
这样,对于每一个节点,求答案的时间复杂度就变成了字典树的深度。这样我们就把总时间复杂度优化为了 \(O(n \log V)\),其中 \(V\) 为边权的值域
代码:
// BLuemoon_
#include <bits/stdc++.h>
using namespace std;
const int kMaxN = 1e6 + 5;
int n, e[kMaxN], ans = -1;
vector<pair<int, int> > g[kMaxN];
struct Trie {
int tot, to[kMaxN][2], ed[kMaxN];
void Insert(int s, int u = 0) {
for (int i = 31; ~i; i--) {
int v = (s >> i) & 1;
if (to[u][v] == 0) {
to[u][v] = ++tot, u = tot;
} else {
u = to[u][v];
}
}
}
int Query(int s, int u = 0, int ret = 0) {
for (int i = 31; ~i; i--) {
int v = (s >> i) & 1;
if (to[u][v ^ 1]) {
ret += (1 << i), u = to[u][v ^ 1];
} else {
u = to[u][v];
}
}
return ret;
}
};
Trie tr;
void DFS(int u, int fa) {
for (auto [v, w] : g[u]) {
if (v != fa) {
e[v] = e[u] ^ w, DFS(v, u);
}
}
}
int main() {
cin >> n;
for (int i = 1, u, v, w; i < n; i++) {
cin >> u >> v >> w, g[u].push_back(make_pair(v, w)), g[v].push_back(make_pair(u, w));
}
DFS(1, 0);
for (int i = 1; i <= n; i++) {
tr.Insert(e[i]);
}
for (int i = 1; i <= n; i++) {
ans = max(ans, tr.Query(e[i]));
}
cout << ans << '\n';
return 0;
}
Part 3 KMP
Knuth–Morris–Pratt 算法(简称KMP算法)是用来解决字符串匹配问题的算法
字符串匹配:查找一个模式串在文本中出现的全部位置,类似于编辑器中的 Ctrl + F
定义一个字符串的 \(\texttt{border}\) 为这个字符串的最长公共真前后缀长度,是不是很绕
举个例子:bcadacbc 它的 \(\texttt{border}\) 为 \(2\),因为它长度为 \(2\) 的前缀和后缀都是 bc,但没有比它更长的公共真前后缀了
用数学语言描述如下(摘自 OI-Wiki):\(\displaystyle\max_{0 \le k < n} \{k :s[1\sim k]=s[(n-k+1)\sim n] \}\),其中 \(s[u\sim v]\) 表示 \(s\) 从第 \(u\) 个字符到第 \(v\) 个字符的子串
对于一个字符串 \(s\) 我们定义其 \(border\) 数组为它的每一个前缀的 \(\texttt{border}\) 值,即 \(border_i=\texttt{border}(s[1\sim i])\)
我们可以在 \(O(n)\) 的时间复杂度内求出一个字符串的 \(border\) 数组
考虑证明两个引理:
引理1:\(border_{i+1}\) 最多为 \(border_i+1\)
证明:从 \(border_i\) 到 \(border_{i+1}\) 字符串只向后增加了一个字符,那么当且仅当 \(s_{border_{i}+1}=s_{i+1}\) 时,\(border_{i+1}\) 取到最大值为 \(border_i+1\),否则只能退而求其次缩小 \(\texttt{border}\) 长度来达到前后缀相等的条件。这幅图可以帮助理解
\[\displaystyle\overbrace{s_1s_2s_3s_4}^{border_i}s_5s_6\cdots s_{i-4}\displaystyle\overbrace{s_{i-3}s_{i-2}s_{i-1}s_i}^{border_i}s_{i+1} \]最好情况是 \(s_5=s_{i+1}\),此时 \(border_{i+1}=border_i+1=4+1=5\),但不可能更大了,否则就要求 \(s_0=s_{i-4}\),但不存在 \(s_0\),所以最大值是 \(border_i+1\)
\[\text{Q.E.D.} \]
引理2:若 \(s_{border_i+1} \ne s_{i+1}\) 那么 \(border_{i+1}\) 的最大值为 \(border_{border_i}+1\)
证明:
(图片来自 OI_Wiki,\(\pi[i]\) 即 \(border_i\),字符串下标从 \(0\) 开始)如图,令 \(border_{border_i-1}=j\),由 \(\texttt{border}\) 的定义可以得到:\(s[0\sim i]\) 的长度为 \(j\) 的后缀和 \(s[0\sim (border_i-1)]\) 的长度为 \(j\) 的后缀相等,因为字符串本身相等,长度相同的后缀也一定相等
又因为 \(j=border_{border_i-1}\),所以 \(s[0\sim (j-1)]=s[(i-j+1)\sim i]\),且 \(j\) 是除 \(border_i\) 外最大的满足该条件的数
所以当 \(s_j=s_{i+1}\) 时,此时 \(border_i\) 的最大值为 \(j+1=border_{border_i-1}+1\)
\[\text{Q.E.D.} \]
于是我们就可以在当前位失配时直接跳到 \(border_i\) 来节省时间了,代码如下(字符串下标从 \(0\) 开始):
vector<int> Border(string c) {
int sz = c.size();
vector<int> ret;
ret.push_back(0);
for (int i = 1, k; i < sz; i++) {
for (k = ret[i - 1]; k && c[i] != c[k]; k = ret[k - 1]) {
}
ret.push_back(k + (c[i] == c[k])); // 跳到最后还失配则border为0
}
return ret;
}
接下来进入 KMP 算法的实现(接下来字符串下标从 \(0\) 开始)
我们令字符串 \(cur=t+\) # \(+s\),\(t\) 为模式串,\(s\) 为文本串,\(n\) 为 \(t_{size}\),\(m\) 为 \(s_{size}\)
求出 \(cur\) 的 \(border\) 数组,当 \(i \in [n+1,n+m]\) 且 \(border_{i}=n\) 时,\(t=cur[i,i+n-1]\),即 \(t\) 在 \(s\) 的 \(i-n-2\sim i-3\) 出现了,这样就找到了一个答案
代码就十分简洁易懂了
void KMP(string c, int sz1, int sz2) {
vector<int> l = Border(c);
for (int i = sz2 + 1; i <= sz1 + sz2; i++) {
if (l[i] == sz2) {
ans[++tot] = (i - sz2 - sz2);
}
}
}
Part 4 字符串哈希
相信大家都知道普通的数字哈希,那么字符串哈希也是同样的道理,算出每一位的权值,用任意进制算出哈希值,就可以快速比较了
单哈希
一般使用 \(131\) 进制,即 \(base=131\)
代码没什么好说的,模拟即可,但需要取模,模数一般为 \(10^9+7\) 或 \(998244353\)
LL Calc(string s, LL ret = 0) {
for (int i = 0; i < s.size(); i++) {
((ret *= base) += (int)(s[i] - 'a' + 1)) %= kP;
}
return ret;
}
双哈希
但有时候单哈希会被某些邪恶的出题人特意构造数据卡掉,所以双哈希就出现了
我们可以使用两个进制和模数来判断两个字符串是否相同,这样同时卡掉两个的概率就几乎没有了
pair<LL, LL> Calc(string s, pair<LL, LL> ret = make_pair(0, 0)) {
for (int i = 0; i < s.size(); i++) {
((ret.first *= base1) += (int)(s[i] - 'a' + 1)) %= kP1, ((ret.second *= base2) += (int)(s[i] - 'a' + 1)) %= kP2;
}
return ret;
}
自然溢出哈希
手写模数是不是很麻烦且容易写错,此时我们就可以使用自然溢出哈希来摆脱取模的困扰
这个方法是利用了 \(2^{64}-1\) 是一个大质数的性质,所以我们可以使用 unsigned long long 来自然溢出使答案可以自动取模这个数
ULL Calc(string s, ULL ret = 0) {
for (int i = 0; i < s.size(); i++) {
(ret *= base) += (int)(s[i] - 'a' + 1);
}
return ret;
}
由于此题不止出现了小写字母,所以可以将 \(base\) 调大,并直接使用 ASCII 码表示
求出哈希值后进行排序,比较相邻两项即可
代码:
// BLuemoon_
#include <bits/stdc++.h>
using namespace std;
using ULL = unsigned long long;
const int base = 503;
int n, a[10005];
string s;
ULL Calc(string s, ULL ret = 0) {
for (int i = 0; i < s.size(); i++) {
(ret *= base) += (int)(s[i]);
}
return ret;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> s, a[i] = Calc(s);
}
sort(a + 1, a + n + 1);
int ans = 0;
for (int i = 1; i < n; i++) {
ans += (a[i] != a[i + 1]);
}
cout << ++ans << endl;
return 0;
}

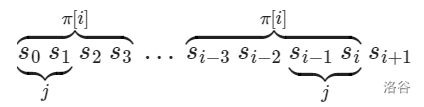

 浙公网安备 33010602011771号
浙公网安备 33010602011771号