BUAA OO 第一单元总结
一、第一次作业
(1)类结构设计
第一次题目架构比较简单,具体结构设计如下(图1):
- 基本数据类型:
Polynomial:用Hashmap<int(指数), BigInteger(系数)>将表达式/项/因子数据内容统一形式- 运算方法:加法
add、乘法mul、乘方pow - 格式化输出:
toString方法将其内容输出(含正项提前处理),addPowerFunc负责将每个项转化为字符串形式。
- 运算方法:加法
- 表达式解析:
Lexer:使用正则表达式(?<num>(?<=[^\\dx)]|^)[+-]?\\d+|x)|(?<opt>\\*\\*|[)(+\\-*])匹配每个有效字符串,得到形如{"-","-","-2","*","(","x",")"}的字符串序列parser:使用递归下降法对得到的字符串序列进行解析,得到表达式/项/因子实例对象。
- 表达式储存
Expr:表达式- 运算方法:
update将terms中的Polynomial相乘后,在乘power次幂并记录到res中;negate将res取负。 - 更新方法:
addTerm增加新的项 - 输出方法:
toString调用res.toString
- 运算方法:
Term:项- 运算方法:
update将factors中的Polynomial相加并记录到res中,negate将res取负。 - 更新方法:
addFactor增加新的因子
- 运算方法:
Factor(接口):包含Expr和ValueFactor- 运算方法:
negate将res取负 - 取值方法:
getRes获得Factor中数据值 - 接口实现类:
Expr:表达式ValueFactor:常数(幂次为0)以及幂函数
- 运算方法:
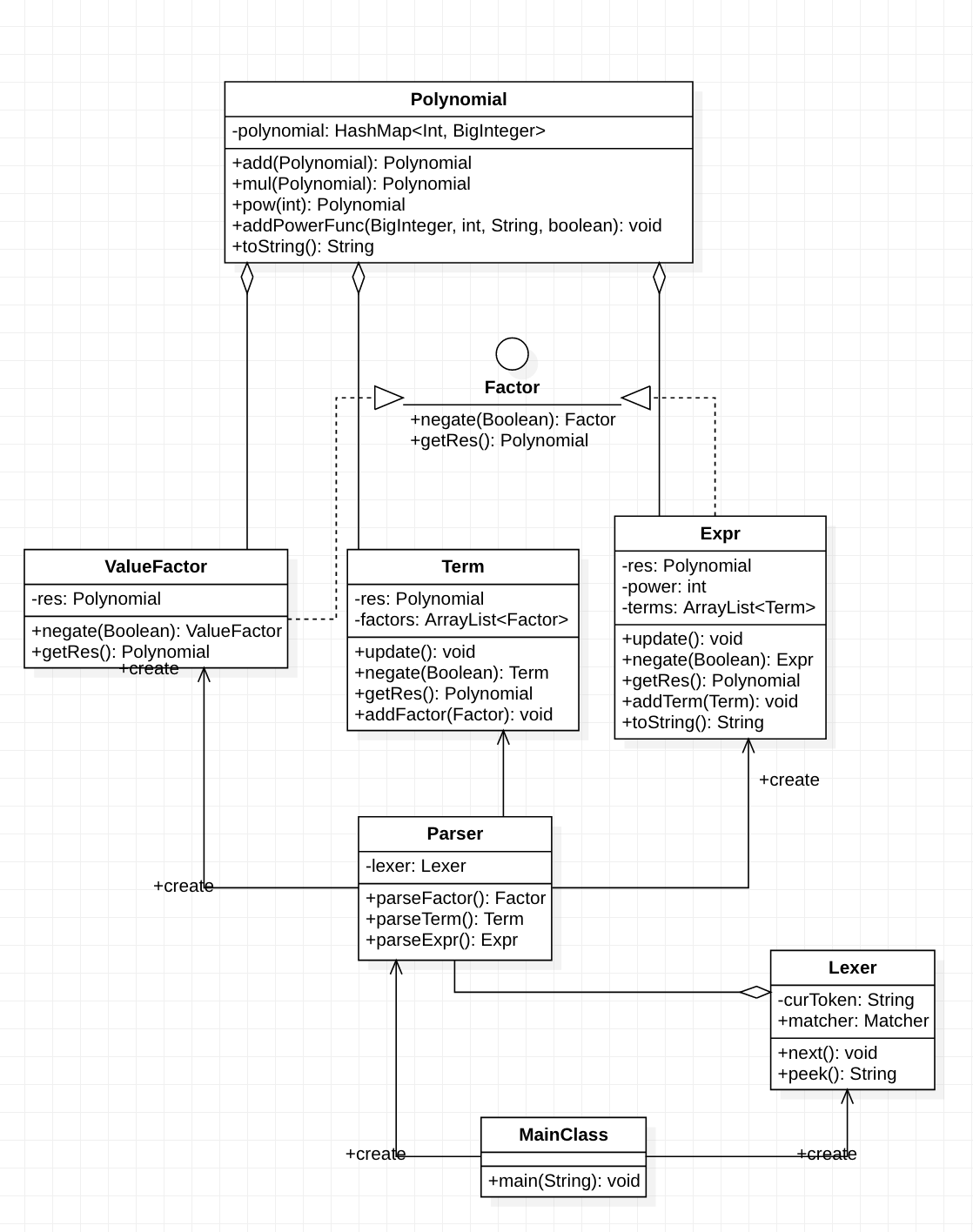
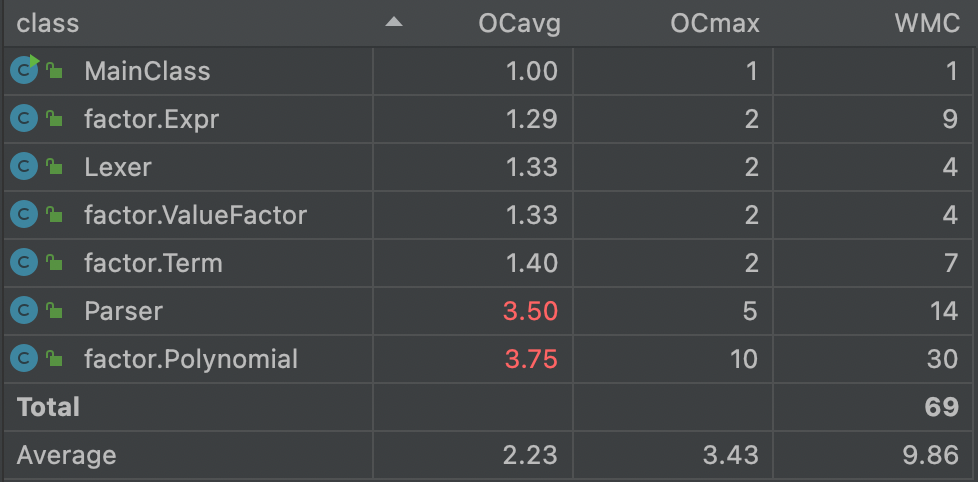
(2)度量分析
从图中可以看出Polynomial和Parser类OCavg较高,高复杂度在于递归调用(Parser)和双重循环(Polynomial)。
(3)Hack情况
- 己方bug分析:本次作业个人在强测和弱侧中均未出现bug
- 对方bug分析:
- 解析
- -时出错
- 解析
二、第二次作业
(1)类结构设计
第二次作业增加了三角函数、自定义函数、求和函数,代码量相较于第一次有明显增长,不过整体架构上没有太大变化。值得一提的是在处理自定义函数/求和函数时,个人的处理方法是先把原表达式以字符串形式储存下来再用类似Parser的方法解析,由于这样Function和Parser的方法有相似之处(也为了后续嵌套表达式处理),因此将Parser和Function进行了合并(由于耦合过高,第三次作业将Function类进行了解耦)
- 基本数据类型:
Polynomial:用Hashmap<Hashmap<Factor, int(指数)>, BigInteger(系数)>将表达式/项/因子数据内容统一形式。其中Factor有且仅有三角函数、幂函数、常数。****- 运算方法:加法
add、乘法mul、乘方pow - 格式化输出:
toString方法将其内容输出(含正项提前处理),addPowerFunc负责将每个项转化为字符串形式。 - 判断相等方法:
hashCode和equal - 化简方法:
replaceSinX2/replaceCosX2:负责形如 \(asin(x)^2+bcos(x)^2+c\) 平方和(其中\(a\)、\(b\)、\(c\)、\(x\))均为任意因子/项。replaceSinX4:负责形如 \(a(sin(x)^4-cos(x)^4)\)的化简。buildSinXnPowers/buildCosXnPowers/buildConstXnPowers:在化简过程中构造含 \(sin(x)^n\) / \(cos(x)^n\) / 去掉对应三角函数的项
- 运算方法:加法
- 表达式解析:
Lexer:使用正则表达式((?<=[^\w)]|^)[+-]?\d+)|(\*\*|[)(+\-*])|(sin|cos|sum)|([a-z,])匹配每个有效字符串,得到形如{"-","-","-2","*","(","x",")"}的字符串序列(New!)Function:- 解析方法:
parseXXX:使用递归下降法对得到的字符串序列进行解析,得到表达式/项/因子实例对象或者对幂次解析。accessSign:对表达式/项首项符号的解析
- 计算方法:
calculate:调用后传入参数,得到自定义函数的值(Expr)。
- 解析方法:
- 表达式储存
Expr:表达式- 运算方法:
updatePower将res乘power次幂并记录到res中;update将terms中的Polynomial相乘后记录到res中;negate将res取负。 - 更新方法:
addTerm增加新的项 - 输出方法:
toString调用res.toString - 化简方法:
simplyfy将调用res.simplyfy - 判断相同方法:
hashCode和equal - 复制方法:
deeplClone创造一个新的Expr
- 运算方法:
Term:项- 运算方法:
update将factors中的Polynomial相加并记录到res中,negate将res取负。 - 更新方法:
addFactor增加新的因子 - 判断相等方法:
hashCode和equal
- 运算方法:
Factor(接口):negate:将res取负getRes:获得Factor中数据值deepClone:深拷贝setPower:设置Factor的幂次- 接口实现类
Expr:表达式- 判断相等方法:
hashCode和equal - 输出方法:
toString
- 判断相等方法:
Var:幂函数- 判断相等方法:
hashCode和equal - 输出方法:
toString
- 判断相等方法:
Constant:常数- 判断相等方法:
hashCode和equal - 输出方法:
toString
- 判断相等方法:
TtrigonometricFactor:三角函数- 判断相等方法:
hashCode和equal - 输出方法:
toString - 子类:
Sin:正弦函数Cos:余弦函数
- 判断相等方法:

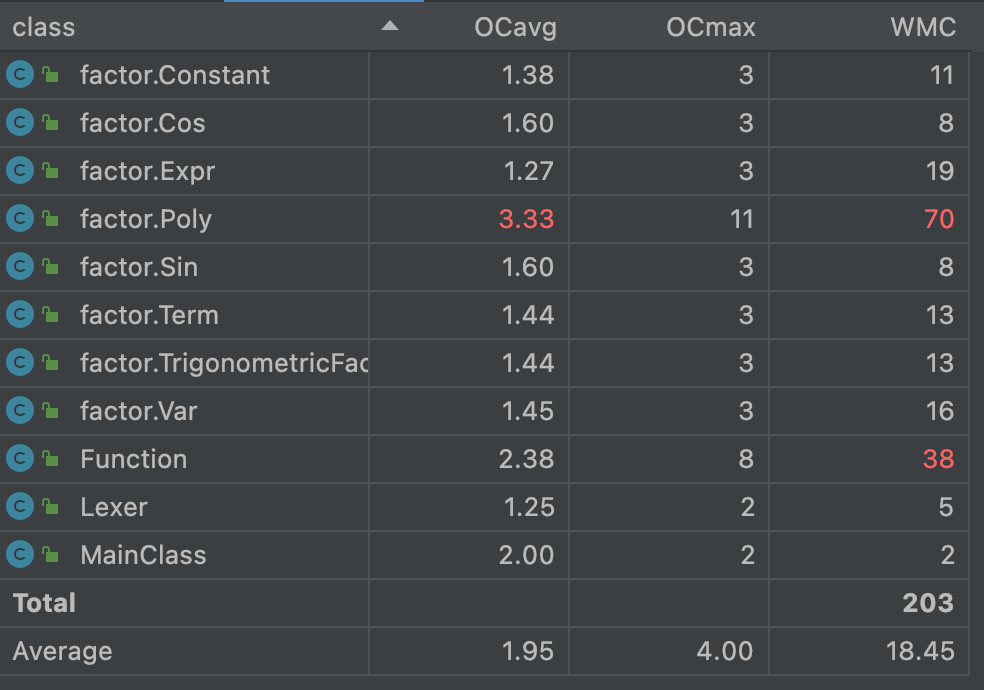
(2)度量分析
从图中可以看出Poly类的OCavg和WMC较高,Function类(原Parser类)的WMC较高,原因同第一次作业。
(3)Hack情况
- 己方bug分析:本次作业个人在强测未出现bug,互测出现两个bug
sin(0)**0解析出错:原因是如果检查到sin(0)时直接返回常数0,未考虑幂次- 化简含
cos(x)**2的表达式时出错:原因是构建时把含cos的项误写成含sin的项
- 对方bug分析:
sin(0)**0解析出错sin(-1)**2解析出错(底数换成-sin(1)后没有考虑幂次对最终符号的影响)
三、第三次作业
第三次作业允许三角函数/自定义函数的嵌套,相较于第二次作业几乎没有改动,仅仅对Poly类和Function类做了解耦,提取了部分方法,同时改变了一些方法/类名,增加可读性。
(1)类结构设计
- 基本数据类型:
Polynomial:用Hashmap<Hashmap<Factor, int(指数)>, BigInteger(系数)>将表达式/项/因子数据内容统一形式。其中Factor有且仅有三角函数、幂函数、常数。****- 运算方法:加法
add、乘法mul、乘方pow - 格式化输出:
toString方法将其内容输出(含正项提前处理),addPowerFunc负责将每个项转化为字符串形式。 - 判断相等方法:
hashCode和equal - 判断数据类型方法:
equalX2、equalConstant、equalExpr
- 运算方法:加法
- PolySimplyfy:化简方法类
handleSinX2/handleCosX2:负责形如 \(asin(x)^2+bcos(x)^2+c\) 平方和(其中\(a\)、\(b\)、\(c\)、\(x\))均为任意因子/项。handleSinX4:负责形如 \(a(sin(x)^4-cos(x)^4)\)的化简。buildSinXnPowers/buildCosXnPowers:在化简过程中构造含 \(sin(x)^n\) / \(cos(x)^n\) / 去掉对应三角函数的项replaceFactor:替换项中的FactorhandleSinXCosX:处理Sin二倍角化简handleCos2X:处理Cos二倍角化简
- 表达式解析:
Lexer:使用正则表达式((?<=[^\w)]|^)[+-]?\d+)|(\*\*|[)(+\-*])|(sin|cos|sum)|([a-z,])匹配每个有效字符串,得到形如{"-","-","-2","*","(","x",")"}的字符串序列(New!)Parser:- 解析方法:
parseXXX:使用递归下降法对得到的字符串序列进行解析,得到表达式/项/因子实例对象或者对幂次解析。accessSign:对表达式/项首项符号的解析
- 解析方法:
Function:- 计算方法:
calculate:调用后传入参数,得到自定义函数的值(Expr)
- 计算方法:
- 表达式储存
Expr:表达式- 运算方法:
updatePower将res乘power次幂并记录到res中;update将terms中的Polynomial相乘后记录到res中;negate将res取负。 - 更新方法:
addTerm增加新的项 - 输出方法:
toString调用res.toString - 化简方法:
simplyfy将调用res.simplyfy - 判断相同方法:
hashCode和equal - 复制方法:
deeplClone创造一个新的Expr
- 运算方法:
Term:项- 运算方法:
update将factors中的Polynomial相加并记录到res中,negate将res取负。 - 更新方法:
addFactor增加新的因子 - 判断相等方法:
hashCode和equal
- 运算方法:
Factor(接口):negate:将res取负getRes:获得Factor中数据值deepClone:深拷贝setPower:设置Factor的幂次- 接口实现类
Expr:表达式- 判断相等方法:
hashCode和equal - 输出方法:
toString
- 判断相等方法:
Var:幂函数- 判断相等方法:
hashCode和equal - 输出方法:
toString
- 判断相等方法:
Constant:常数- 判断相等方法:
hashCode和equal - 输出方法:
toString
- 判断相等方法:
TtrigonometricFactor:三角函数- 判断相等方法:
hashCode和equal - 输出方法:
toString - 子类:
Sin:正弦函数normalize:标准化方法,将Sin中内容转化为统一格式(改变正负)
Cos:余弦函数normalize:标准化方法,将Cos中内容转化为统一格式(改变正负)
- 判断相等方法:

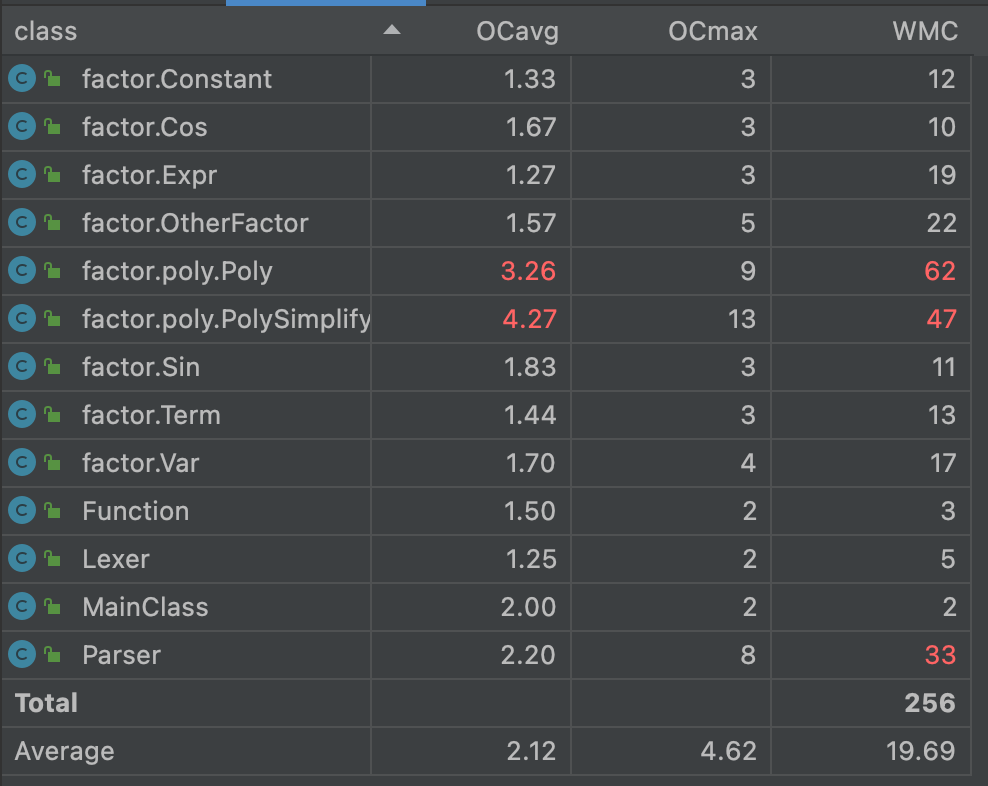
(2)度量分析
从图中可以看出Poly类和PolySimplyfy的OCavg和WMC较高,Parser的WMC较高,Poly和Parser原因同第一次作业,PolySimplyfy原因为每次化简时需要遍历所有键值对,同时一直化简到无法化简为止。
(3)Hack情况
本次强测结果比较惨痛,根本原因在于课下测试不充分。
- 己方bug分析:本次作业个人在强测和互测共出现3个bug
Poly中equalX2方法出错:未考虑x^2前系数-sin(x)**0解析出错:未考虑三角函数本身负号getContentPoly方法复杂度过高,需要多次调用mul等函数,导致三角函数嵌套过多是TLE
- 对方bug分析:
- 用
int类型 解析求和函数的起始或结束常数 sin((-x*x))化简出错sum中出现i**0出错
- 用
四、架构设计体验
在第一次作业时,个人采取的方法为传统的用栈解析表达式,结果中测没过(后来发现是正则表达式的问题)。于是又用递归下降方法重新做了一遍,结果三次作业都没有进行大规模重构。现在想想如果采取用栈解析表达式的方法会导致方法冗长,每加入新的运算符都要对多个函数进行改写,不符合面向对象设计思想
在第二次作业时遇到最大的问题就是如何表示数据(多项式),在分析第一次架构的表示数据方法使用了Hashmap<Hashmap<Factor, int>, BigInteger>对数据进行存储。同时,完成基本代码编写花费了近乎一天半的时间对代码进行小范围重构(例如提取函数、分解函数、提取父类、重命名等等)(这一过程中《重构:改善既有代码设计》一书对我启发颇深)
在第三次作业时由于第二次作业的代码基本上已经能满足需求,所以在简单对部分类进行解耦后,花费了更多时间在提高性能上,但是却疏于对更改后的代码进行测试,导致出现了细微但较为严重的BUG,应当进行深刻反省。
五、感想&小结
Unit1说实话个人做起来还是比较艰难的,主要原因有以下几点:
- 对文法分析的不熟悉,花费了6~7个小时理解并实现了递归下降法
- 对面向对象的思想不熟悉,导致一部分代码在一开始不符合面向对象的思想,花费了较多时间阅读《重构:改善既有代码设计》并进行重构
- 对测试方法不熟悉,导致第三次作业出现了严重BUG
虽然艰难,不过在完成本单元的学习后还是收获满满:)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号