哈夫曼编码例题

某电文中由A、B、C、D、E、F、G共7个字母组成,使用的频度分别0.1、0.05、0.25、0.15、0.1、0.2、0.15。

(1)构造哈夫曼树。

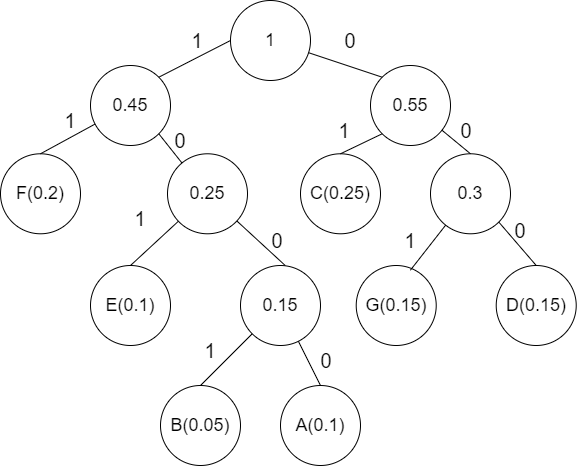
(2)列表写出操作码的等长编码、哈夫曼编码和只用两种最短码长的扩展编码。

操作码	频度	等长编码	哈夫曼编码	扩展编码
A	0.1	000	1000	1110
B	0.05	001	1001	1111
C	0.25	010	01	00
D	0.15	011	000	1100
E	0.1	100	101	1101
F	0.2	101	11	01
G	0.15	110	001	10

(3)分别计算等长编码、哈夫曼编码、扩展编码的平均码长。

等长编码长度：3

哈夫曼编码平均长度：
\( (0.1 + 0.05) \times 4 + (0.15 + 0.1 + 0.15) \times 3 + (0.25 + 0.2) \times 2 = 2.7 \)

扩展码平均长度：
\( (0.1 + 0.05 + 0.15 + 0.1) \times 4 + (0.25 + 0.2 + 0.15) \times 2 = 2.8 \)