frequency Time

频率域的

%matlab
Fs = 1000;                    % Sampling frequency
T = 1/Fs;                     % Sample time
L = 1000;                     % Length of signal
t = (0:L-1)*T;                % Time vector
% Sum of a 50 Hz sinusoid and a 120 Hz sinusoid
x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); 
y = x + 2*randn(size(t));     % Sinusoids plus noise
plot(Fs*t(1:50),y(1:50))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('time (milliseconds)')

NFFT = 2^nextpow2(L); % Next power of 2 from length of y
Y = fft(y,NFFT)/L;
f = Fs/2*linspace(0,1,NFFT/2+1);

% Plot single-sided amplitude spectrum.
plot(f,2*abs(Y(1:NFFT/2+1))) 
title('Single-Sided Amplitude Spectrum of y(t)')
xlabel('Frequency (Hz)')
ylabel('|Y(f)|')

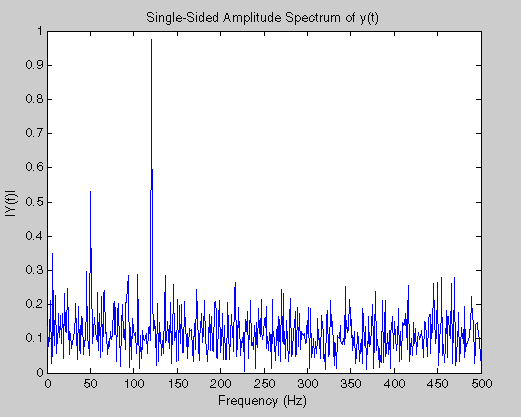
频谱上的噪声是由于随机噪声导致的

时域的波形变换成频域中的一个个频率，下一张图也称为频谱图。
正弦波频率分量及其幅度的集合称为频谱，每一分量称为谐波；
在频域中，对波形的描述变为不同正弦波频率值的集合。每一个频率分量都有相关的幅度及相位，把所有这些频率值及其幅度值的集合称为波形的频谱。
理解关键点：
1，每个频率对应时域波形的一个正弦波分量。
2，每个频率的幅值不同，其计算方式见下面的An公式。频域中多个频率的幅值叠加后得到 时域中的最大幅值1（当时域上某个时间点时，所有正弦波分量会达到同相，此时所有正弦波分量波的叠加会达到时域中的最大幅值）。
3，叠加的方法见“傅里叶反变换”部分。

由于各正弦波的频率、初相位、幅度都不同，所以叠加后的波形很可能不再是正弦信号，但一定是周期信号。且周期、频率=基波正弦波的周期、频率。

假设有一数据由以下方程生成，这里 x=np.linspace(0,1,1000)，由于数据长度只有1000，频率3000的信号将不会显示在图上，而是以低频信号出现
y=7np.sin(2np.pi180x) + 2.8np.sin(2np.pi3000x)+5.1np.sin(2np.pi450x)