深入解析：贪心算法 | 每周8题（二）

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
示例 1：
输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
示例 2：
输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

思路：在最低时买入，最高时卖出。遍历prices数组，从第一个开始，用每个值将去当前最小值（从第一个开始）得到此时利润，每次保留当前最大利润，并且更新最小值，直到遍历结束。

代码：

class Solution {
public:
    int maxProfit(vector& prices) {
        int ret=0;
        int premin=INT_MAX;
        for(int i=0;i


1.2买卖股票的最佳时机 II（可以多次买卖）
题目：
给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。
在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。然而，你可以在 同一天 多次买卖该股票，但要确保你持有的股票不超过一股。
返回 你能获得的 最大 利润 。
示例 1：
输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。
示例 2：
输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。
示例 3：
输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0。
思路：上涨前买，下跌前卖。这里提供两种方法(●'◡'●)
法一：双指针：遍历prices数组，用下一个元素j的值减去当前元素i的值，若为正数，加上此时利润；为负数，将此时的i移动到j的位置（贪心），继续上面操作，直至遍历结束。
法二：只加盈利部分：遍历prices数组，用下一个元素的值减去当前元素i的值，若为正数，加上此时利润；否则看下一个值，直至遍历结束。
代码：
//法一：双指针
class Solution {
public:
    int maxProfit(vector& prices) {
        int ret=0;
        for(int i=0;iprices[j]))j++;
           ret+=prices[j]-prices[i];
           i=j;
        }
        return ret;
    }
};
/*
法二：每一天
class Solution {
public:
    int maxProfit(vector& prices) {
        int ret=0;
        for(int i=0;i+10)ret+=prices[i+1]-prices[i];
        }
        return ret;
    }
};
*/
1.3按身高排序
题目：
（tip:本题严格来说不算是贪心题，但是为下面一题做铺垫，咱可以看一下，掠过也行哈）
给你一个字符串数组 names ，和一个由 互不相同 的正整数组成的数组 heights 。两个数组的长度均为 n 。
对于每个下标 i，names[i] 和 heights[i] 表示第 i 个人的名字和身高。
请按身高 降序 顺序返回对应的名字数组 names 。
示例 1：
输入：names = ["Mary","John","Emma"], heights = [180,165,170]
输出：["Mary","Emma","John"]
解释：Mary 最高，接着是 Emma 和 John 。
示例 2：
输入：names = ["Alice","Bob","Bob"], heights = [155,185,150]
输出：["Bob","Alice","Bob"]
解释：第一个 Bob 最高，然后是 Alice 和第二个 Bob 。
提示：
n == names.length == heights.length
1 <= n <= 103
1 <= names[i].length <= 20
1 <= heights[i] <= 105
names[i] 由大小写英文字母组成
heights 中的所有值互不相同
思路：用一个索引数组（因为身高与姓名相对应，若身高顺序变了，不能返回原来的姓名）表示身高数组中的元素。将索引中的元素按照身高由高到低排序，再让姓名数组按照索引中顺序输出。
代码：
class Solution {
public:
    vector sortPeople(vector& names, vector& heights) {
        //建立一个下标数组
        int n=names.size();
        vectorindex(n);
        for(int i=0;iheights[j];});
        //取出下标对应的姓名
        vectorstrs;
        for(auto e:index)strs.push_back(names[e]);
        return strs;
    }
};
1.4优势洗牌
题目：
给定两个长度相等的数组 nums1 和 nums2，nums1 相对于 nums2 的优势可以用满足 nums1[i] > nums2[i] 的索引 i 的数目来描述。
返回 nums1 的 任意 排列，使其相对于 nums2 的优势最大化。
示例 1：
输入：nums1 = [2,7,11,15], nums2 = [1,10,4,11]
输出：[2,11,7,15]
示例 2：
输入：nums1 = [12,24,8,32], nums2 = [13,25,32,11]
输出：[24,32,8,12]
tip:本题的“优势”其实和“田忌赛马”差不多，就是体现 “扬长避短、优化资源配置” 的智慧。
咱们在这儿补充一下“田忌赛马”的故事：
田忌与齐王赛马，设上、中、下三等级马对决，每次均以同等级马比拼，田忌因每一级马匹均稍逊齐王，屡赛屡输。孙膑献策：以田忌下等马对齐王上等马（先输一场），再用上等马对其中等马、中等马对其下等马。最终三局两胜，田忌获胜。
思路：让nums1中最小的数去消耗nums2中最大的数。先用一个索引数组存放nums2（因为nums2中的元素顺序不能变），再将索引数组按照nums2中元素大小排升序，将nums1中的元素也排升序。然后遍历nums1和索引所对应的nums2元素大小，若满足 nums1[i] > nums2[index] ,比较下一个元素；否则，将 nums1[i]对应到索引数组index的最后面。
代码：
class Solution {
public:
    vector advantageCount(vector& nums1, vector& nums2) {
        //将nums1排序（升序）
        sort(nums1.begin(),nums1.end());
        //构造num2的下标数组index2
        int n=nums2.size();
        vectorindex2(n);
        for(int i=0;iret(n);
        int left=0,right=n-1;
        for(auto e:nums1)
        {
            if(e>nums2[index2[left]])ret[index2[left++]]=e;
            else ret[index2[right--]]=e;
        }
        return ret;
    }
};
1.5最长回文串
题目：
给定一个包含大写字母和小写字母的字符串 s ，返回 通过这些字母构造成的 最长的 回文串 的长度。
在构造过程中，请注意 区分大小写 。比如 "Aa" 不能当做一个回文字符串。
示例 1:
输入:s = "abccccdd"
输出:7
解释:
我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。
示例 2:
输入:s = "a"
输出:1
解释：可以构造的最长回文串是"a"，它的长度是 1。
提示:
1 <= s.length <= 2000
s 只由小写 和/或 大写英文字母组成
思路：将所有偶数个数的字母均加入到回文字符串当中，每加一次，长度加一。若还有奇数的字母，再最终长度上再＋1。
代码：
class Solution {
public:
    int longestPalindrome(string s) {
//计数，用数组模拟哈希表
        nt hash[127]={0};
        for(auto e:s)hash[e]++;
        int ret=0;
        for(auto e:hash)ret+=e/2*2; //偶数加，奇数舍
        return ret

1.6增减字符串匹配
题目：
由范围 [0,n] 内所有整数组成的 n + 1 个整数的排列序列可以表示为长度为 n 的字符串 s ，其中:
如果 perm[i] < perm[i + 1] ，那么 s[i] == 'I'
如果 perm[i] > perm[i + 1] ，那么 s[i] == 'D'
给定一个字符串 s ，重构排列 perm 并返回它。如果有多个有效排列perm，则返回其中 任何一个 。
示例 1：
输入：s = "IDID"
输出：[0,4,1,3,2]
示例 2：
输入：s = "III"
输出：[0,1,2,3]
示例 3：
输入：s = "DDI"
输出：[3,2,0,1]
思路：若输入'I'，将其和目前最小的匹配；输入'D'和最大的匹配。
代码：
class Solution {
public:
    vector diStringMatch(string s) {
        int left=0,right=s.size();//取[0，n]包含n;
        vectorret;
        for(int i=0;i

1.7分发饼干
题目：
假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。
对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是满足尽可能多的孩子，并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3 个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是 1，你只能让胃口值是 1 的孩子满足。
所以你应该输出 1。
示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2 个孩子的胃口值分别是 1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出 2。
思路：给每个孩子都分配，目前可以满足其胃口的最小饼干尺寸。先将孩子胃口、饼干尺寸从小到大排序。先设置一个结果值。然后，遍历孩子胃口，饼干大小，若符合胃口，结果值＋1；反之，舍去那个饼干，接着遍历，直至饼干或孩子遍历结束。
代码：
class Solution {
public:
    int findContentChildren(vector& g, vector& s) {
        int n=g.size(),m=s.size();
        int ret=0;
        sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        for(int i=0,j=0;i= g[i]时，j会停滞
        {
            while(j

1.8最优除法
题目：
给定一正整数数组nums，nums 中的相邻整数将进行浮点除法。
例如，nums = [2,3,4]，我们将求表达式的值 "2/3/4"。
但是，你可以在任意位置添加任意数目的括号，来改变算数的优先级。你需要找出怎么添加括号，以便计算后的表达式的值为最大值。
以字符串格式返回具有最大值的对应表达式。
注意：你的表达式不应该包含多余的括号。
示例 1：
输入: [1000,100,10,2]
输出: "1000/(100/10/2)"
解释: 1000/(100/10/2) = 1000/((100/10)/2) = 200
但是，以下加粗的括号 "1000/((100/10)/2)" 是冗余的，
因为他们并不影响操作的优先级，所以你需要返回 "1000/(100/10/2)"。

其他用例:
1000/(100/10)/2 = 50
1000/(100/(10/2)) = 50
1000/100/10/2 = 0.5
1000/100/(10/2) = 2
示例 2:
输入: nums = [2,3,4]
输出: "2/(3/4)"
解释: (2/(3/4)) = 8/3 = 2.667
可以看出，在尝试了所有的可能性之后，我们无法得到一个结果大于 2.667 的表达式。
说明:
1 <= nums.length <= 10
2 <= nums[i] <= 1000
对于给定的输入只有一种最优除法。
思路：若数字数组中元素大于2个，在第二个数字前加一个'('，并再最后加一个')'。本题这样添加括号是因为（“除除得乘”）
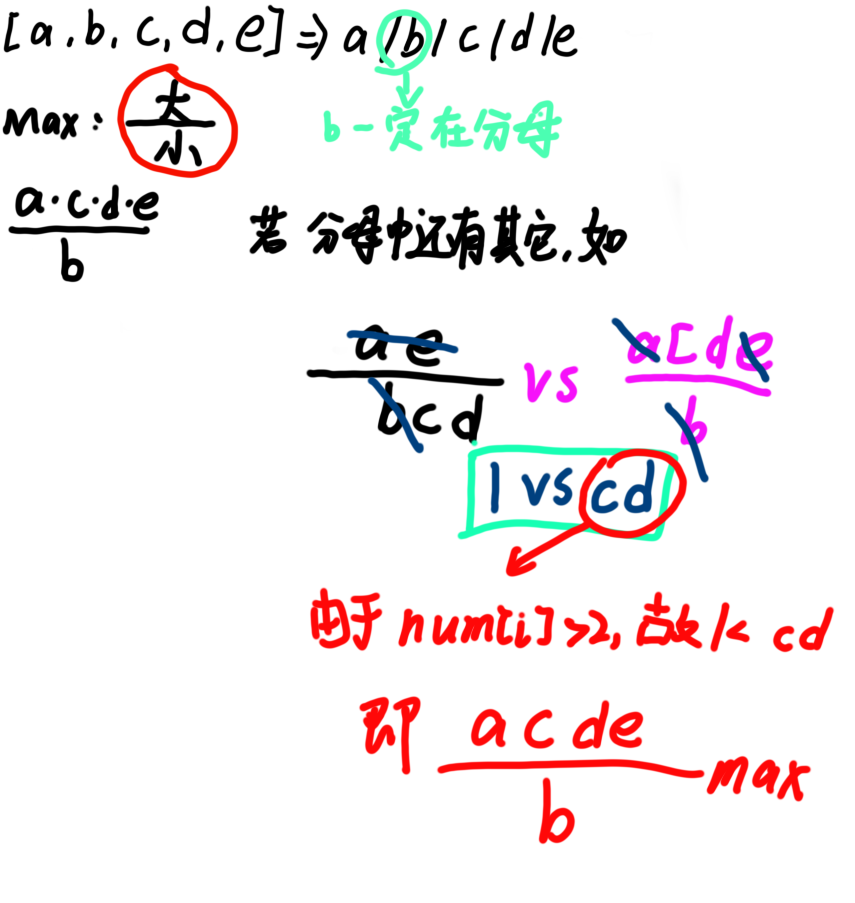
代码：
class Solution {
public:
    string optimalDivision(vector& nums) {
        int n=nums.size();
        if(n==1)return to_string(nums[0]);
        else if(n==2) return to_string(nums[0])+'/'+to_string(nums[1]);
        else
        {
            string ret =to_string(nums[0])+"/("+to_string(nums[1]); //注意这里右边是一个字符串，左边不能定义成数组
            for(int i=2;i

2.小结
本文通过力扣例题详解贪心算法的应用场景与解题思路。主要内容包括：1. 股票买卖问题（单次/多次交易策略）；2. 身高排序与田忌赛马式的优势洗牌；3. 构造最长回文串；4. 增减字符串匹配；5. 分发饼干的最优分配；6. 数学表达式的最优括号添加。解题核心在于抓住局部最优解，通过双指针、排序等技巧实现全局优化。
本周的就讲解到这里O(∩_∩)O
如果想了解更多算法题与思路，欢迎点赞收藏，咱们下周见

posted on 2025-11-04 18:57 blfbuaa 阅读(4) 评论(0) 收藏举报