关于矩阵
前言:
刚学矩阵...
确实有点晚了 把笔记补一下
以矩阵乘法为主 再加一点板子题
矩阵
矩阵是一个数字阵列 如一个 \(n\) 行 \(r\) 列的矩阵表示为:
\[\begin{bmatrix} a_{11} & a_{12} & a_{13} & ... & a_{1r} \\ a_{21} & a_{22} & a_{23} & ... & a_{2r} \\ ... \\ a_{n1} & a_{n2} & a_{n3} & ... & a_{nr}\end{bmatrix}
\]
其实就是一个二维数组... 没什么好说的
特殊的:
行数和列数相等的矩阵称之为方阵
单位矩阵: 主对角线上的元素都是 \(1\) 其余元素都为 \(0\) 的 \(n\) 阶矩阵 称为 \(n\) 阶单位矩阵 记作 \(I\) 或 \(E\)
如:
\[\begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1\end{bmatrix}
\]
在矩阵乘法中 单位矩阵有着和一般的乘法中的 \(1\) 一样的作用
矩阵的运算
加法与减法
将两个矩阵对应位置上的数相加减 其中作差或作和的矩阵以及运算得到的矩阵都是 \(n\) 行 \(m\) 列 如:
\[\begin{bmatrix}5 & 4 & 3 \\ 2 & 1 & 3 \end{bmatrix} + \begin{bmatrix}2 & 4 & 3 \\ 2 & 5 & 6 \end{bmatrix} =
\begin{bmatrix}7 & 8 & 6 \\ 4 & 6 & 9 \end{bmatrix}
\]
\[\begin{bmatrix}5 & 4 & 3 \\ 2 & 1 & 3 \end{bmatrix} - \begin{bmatrix}2 & 4 & 3 \\ 2 & 5 & 6 \end{bmatrix} =
\begin{bmatrix}3 & 0 & 0 \\ 0 & -4 & -3 \end{bmatrix}
\]
这个比较简单 代码就不放了
乘法
设 \(A\) \(B\) 为两个矩阵 令 \(C\) = \(A \times B\) 则有:
- \(A\) 的列数等于 \(B\) 的行数
- 若 \(A\) 为一个 \(n \times r\) 的矩阵 \(B\) 为一个 \(r \times m\) 的矩阵 则 \(C\) 为一个 \(n \times m\) 的矩阵
- \(C_{i, j} = \sum_{k = 1}^{r}a_{i, k} \times b_{k, i}\)
例如:
\(A = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix}\) \(B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\end{bmatrix}\) \(C = A \times B\)
\[C = A \times B = \begin{bmatrix} 1 \times 1 + 4 \times 4 & 1 \times 2 + 4 \times 5 & 1 \times 3 + 4 \times 5 \\ 2 \times 1 + 5 \times 4 & 2 \times 2 + 5 \times 5 & 2 \times 3 + 5 \times 6 \\ 3 \times 1 + 6 \times 4 & 3 \times 2 + 6 \times 5 & 3 \times 3 + 6 \times 6\end{bmatrix} = \begin{bmatrix} 17 & 22 & 27 \\ 22 & 29 & 36 \\ 27 & 36 & 45\end{bmatrix}
\]
代码:
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
for(int k = 1; k <= r; k++)
a[i][j] += b[i][k] * c[k][j];
另外的:
- 矩阵乘法不满足交换律
- 矩阵乘法满足结合律
- 矩阵乘法满足左分配律
- 矩阵乘法满足右分配律
矩阵乘幂
矩阵乘幂的条件是这个矩阵是一个方阵
矩阵乘法满足结合律 所以可以用快速幂
矩阵乘法的快速幂
矩阵乘法可以通过重载运算符实现 这样就与普通的快速幂完全一样
板子题: P3390 【模板】矩阵快速幂
代码:
/*
Time: 2.16
Worker: Blank_space
Source: P3390 【模板】矩阵快速幂
*/
/*--------------------------------------------*/
#include<cstdio>
#include<cstring>
#define int long long
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int n, p;
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
struct node {
int a[110][110];
node() {memset(a, 0, sizeof a);}
void scan() {
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++) a[i][j] = read();
}
void build() {for(int i = 1; i <= n; i++) a[i][i] = 1;}
}m;
node operator * (const node &x, const node &y) {
node z;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
for(int k = 1; k <= n; k++)
z.a[i][j] = (z.a[i][j] + x.a[i][k] * y.a[k][j] % mod) % mod;
return z;
}
/*----------------------------------------函数*/
main() {
n = read(); p = read(); m.scan();
node ans; ans.build();
while(p)
{
if(p & 1) ans = ans * m;
m = m * m; p >>= 1;
}
for(int i = 1; i <= n; puts(""), i++)
for(int j = 1; j <= n; j++) printf("%lld ", ans.a[i][j]);
return 0;
}
矩阵乘法的应用
常见的应用是用于优化递推或者是 \(DP\)
下面看一下例题
P1962 斐波那契数列
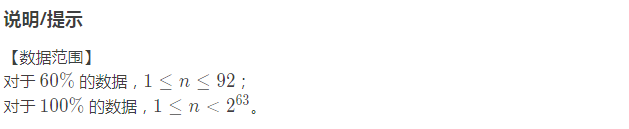
思路:
看一眼想到的肯定是 \(O(n)\) 递推 但是看一下数据范围 他连 \(O(n)\) 的复杂度都卡掉了 这就提示我们要用矩阵加速
斐波那契的递推式是 \(f_i = f_{i - 1} + f_{i - 2}\) 也就是当前项的结果只与前两项有关 我们构造一个 \(1 \times 2\) 的矩阵
设 \(f_i = \begin{bmatrix} f_{i - 1} & f_{i - 2}\end{bmatrix}\)
现在我们希望用这个矩阵乘上另一个矩阵 得到斐波那契数列的下一项 即:
\[\begin{bmatrix} f_{i - 1} & f_{i - 2}\end{bmatrix} \times A = \begin{bmatrix} f_i & f_{i - 1}\end{bmatrix}
\]
关键在于确定这个 \(A\) 是什么
两个矩阵要想相乘 第一个矩阵的列数一定要等于第二个矩阵的行数 而答案矩阵的列数又取决于第二个矩阵的列数 所以不难得到第二个矩阵是 \(2 \times 2\) 的
设:
\[A = \begin{bmatrix} a & b \\ c & d\end{bmatrix}
\]
\[\begin{bmatrix} f_{i - 1} & f_{i - 2}\end{bmatrix} \times \begin{bmatrix} a & b \\ c & d\end{bmatrix} = \begin{bmatrix} af_{i - 1} + cf_{i - 2} & bf_{i - 1} + df_{i - 2}\end{bmatrix} = \begin{bmatrix} f_i & f_{i - 1}\end{bmatrix}
\]
即:
\[\begin{bmatrix} af_{i - 1} + cf_{i - 2} & bf_{i - 1} + df_{i - 2}\end{bmatrix} = \begin{bmatrix} 1f_{i - 1} + 1f_{i - 2} & 1f_{i - 1} + 0f_{i - 2}\end{bmatrix}
\]
所以:
\[A = \begin{bmatrix} 1 & 1\\ 1 & 0\end{bmatrix}
\]
斐波那契数的矩阵每次乘上 \(A\) 都可以得到数列中的下一项
这样 我们可以通过 \(\begin{bmatrix} f_1 & f_2\end{bmatrix}\) 乘上 \(A^{n - 1}\) 来快速的计算斐波那契数列中的第 \(n\) 项
因为矩阵的乘法是满足结合律的 所以可以通过矩阵快速幂先算出 \(A^{n- 1}\)
代码:
/*
Time: 2.16
Worker: Blank_space
Source: P1962 斐波那契数列
*/
/*--------------------------------------------*/
#include<cstdio>
#include<cstring>
#define int long long
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int x;
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
struct node {
int n, m, a[10][10];
node() {memset(a, 0, sizeof a);}
void build() {n = m = 2; a[1][1] = a[1][2] = a[2][1] = 1;}
void _build() {n = m = 2; a[1][1] = a[2][2] = 1;}
void pare() {n = 1; m = 2; a[1][1] = a[1][2] = 1;}
}d;
node operator * (const node &x, const node &y) {
node z; z.n = x.n; z.m = y.m;
for(int i = 1; i <= z.n; i++)
for(int j = 1; j <= z.m; j++)
for(int k = 1; k <= x.m; k++)
z.a[i][j] = (z.a[i][j] + x.a[i][k] * y.a[k][j] % mod) % mod;
return z;
}
/*----------------------------------------函数*/
signed main() {
x = read() - 1; d.pare(); node res, ans; res.build(); ans._build();
while(x)
{
if(x & 1) ans = ans * res;
res = res * res;
x >>= 1;
}
ans = ans * d;
printf("%lld", ans.a[1][1]);
return 0;
}
P1939 【模板】矩阵加速（数列）
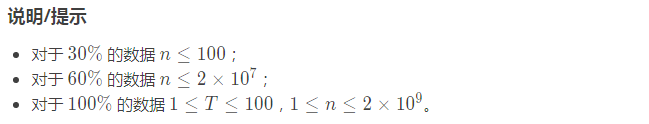
思路:
矩阵加速的模板题 与上面的题目相似 不过初始矩阵变成了 \(1 \times 3\)
设:
\[\begin{bmatrix}f_{i - 1} & f_{i - 2} & f_{i - 3}\end{bmatrix} \times A = \begin{bmatrix}f_i & f_{i - 1} & f_{i - 2}\end{bmatrix}
\]
设:
\[A = \begin{bmatrix}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{bmatrix}
\]
\[\begin{bmatrix}f_{i - 1} & f_{i - 2} & f_{i - 3}\end{bmatrix} \times \begin{bmatrix}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{bmatrix} = \begin{bmatrix}a_{11}f_{i - 1} + a_{21}f_{i - 2} + a_{31}f_{i - 3} & a_{12}f_{i - 1} + a_{22}f_{i - 2} + a_{32}f_{i - 3} & a_{13}f_{i - 1} + a_{23}f_{i - 2} + a_{33}f_{i - 3}\end{bmatrix}
\]
\[\begin{bmatrix}a_{11}f_{i - 1} + a_{21}f_{i - 2} + a_{31}f_{i - 3} & a_{12}f_{i - 1} + a_{22}f_{i - 2} + a_{32}f_{i - 3} & a_{13}f_{i - 1} + a_{23}f_{i - 2} + a_{33}f_{i - 3}\end{bmatrix} = \begin{bmatrix}f_i & f_{i - 1} & f_{i - 2}\end{bmatrix}
\]
可以求得:
\[A = \begin{bmatrix}1 & 0 & 1\\1 & 0 & 0 \\ 0 & 1 & 0\end{bmatrix}
\]
上矩阵快速幂直接搞就行了
代码:
/*
Time: 2.16
Worker: Blank_space
Source: P1939 【模板】矩阵加速（数列）
*/
/*--------------------------------------------*/
#include<cstdio>
#include<cstring>
#define int long long
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int T;
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
struct node {
int n, m, a[10][10];
node() {memset(a, 0, sizeof a);}
void build() {n = 3; m = 3; a[1][1] = a[1][3] = a[2][1] = a[3][2] = 1;}
void _build() {n = 3; m = 3; a[1][1] = a[2][2] = a[3][3] = 1;}
void pare() {n = 1; m = 3; a[1][1] = 1; a[1][2] = 2; a[1][3] = 3;}
}d;
node operator * (const node &x, const node &y) {
node z; z.n = x.n; z.m = y.m;
for(int i = 1; i <= z.n; i++)
for(int j = 1; j <= z.m; j++)
for(int k = 1; k <= x.m; k++)
z.a[i][j] = (z.a[i][j] + x.a[i][k] * y.a[k][j] % mod) % mod;
return z;
}
node power(node x, int p) {
node _res; _res._build();
while(p)
{
if(p & 1) _res = _res * x;
x = x * x;
p >>= 1;
}
return _res;
}
/*----------------------------------------函数*/
signed main() {
T = read(); d.pare();
for(int i = 1; i <= T; i++)
{
node res; res.build();
int x = read();
node ans = power(res, x - 1);
ans = ans * d;
printf("%lld\n", ans.a[1][1]);
}
return 0;
}
浙公网安备 33010602011771号