从SVD到推荐系统
最近在学习推荐系统(Recommender System),跟大部分人一样,我也是从《推荐系统实践》学起,同时也想跟学机器学习模型时一样使用几个开源的python库玩玩。于是找到了surprise,挺新的,代码没有sklearn那么臃肿,我能看的下去,于是就开始了自己不断的挖坑。
这篇文章介绍基于SVD的矩阵分解推荐预测模型。一开始我还挺纳闷,SVD不是降维的方法嘛?为什么可以用到推荐系统呢?研究后,实则异曲同工。
有关SVD推导可以看这篇文章:降维方法PCA与SVD的联系与区别
了解推荐系统的人一定会知道协同过滤算法!
协同过滤算法主要分为两类,一类是基于领域的方法(neighborhood methods),另一类是隐语义模型(latent factor models),后者一个最成功的实现就是矩阵分解(matrix factorization),矩阵分解我们这篇文章使用的方法就是SVD(奇异值分解)
提问❓:SVD在推荐系统中到底在什么位置呢?
举手🙋♂️:推荐系统 -> 协同过滤算法 -> 隐语义模型 -> 矩阵分解 -> SVD
一、Singular Value Decomposition(SVD)
Guide
SVD的思想在推荐系统中用得很巧妙,我们借助下面这个表来理解:
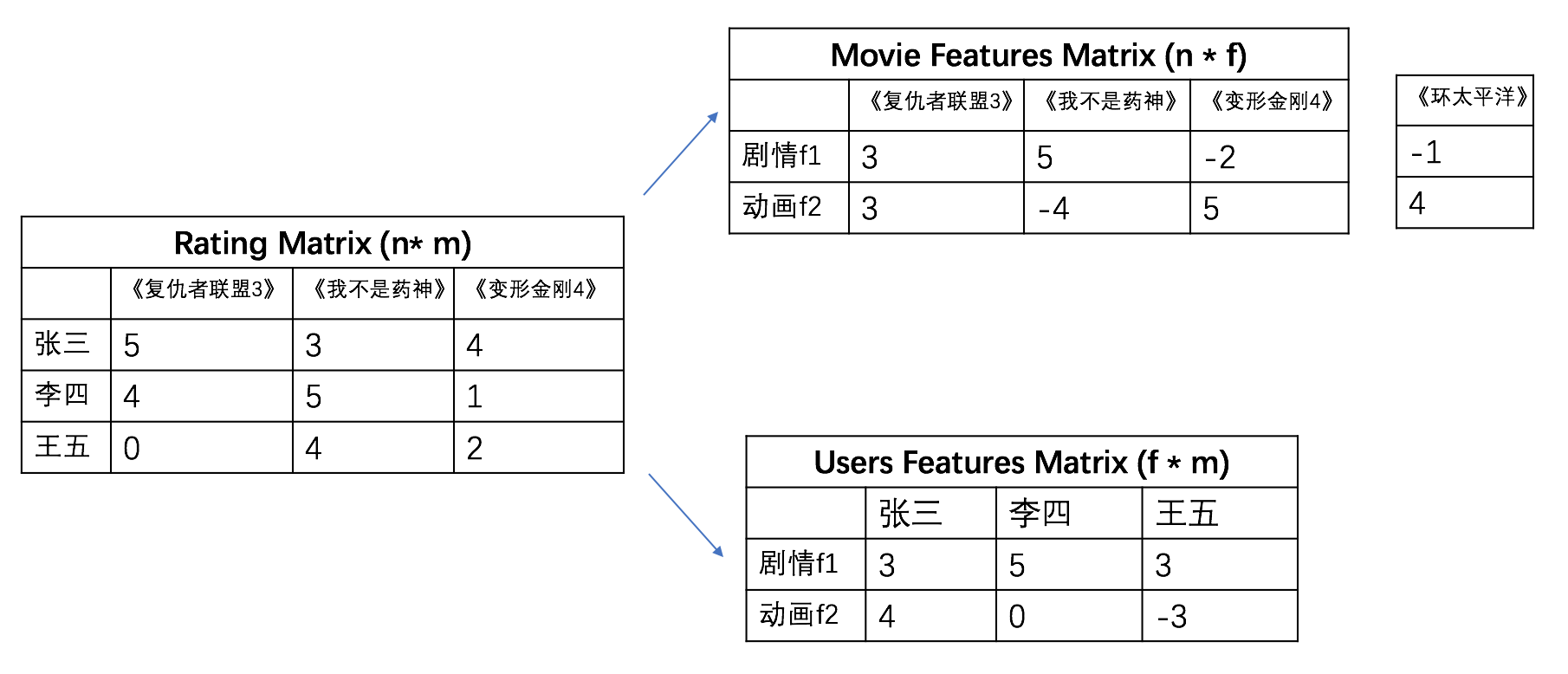
上图有三幅小图,我们来按顺序看(图中的数字请不要纠结于具体数值)。左中图每行代表一个人,每列代表一部电影。每一个数字对应一个人给一部电影的评分,如李四的给《我不是药神》评分为5,给《变形金刚4》的评分为1。
假设我们的目的是给图中的李四推荐电影,你只知道他对这三部电影的评分。这似乎很难,但是设想如果我们知道李四喜欢电影的类型,这样是不是就更好推荐了! 我们的信息量有限,但是并不是少到离谱,所以能不能通过仅有的信息推测出李四喜欢电影的类型呢?
SVD就是做这个事的,继续看右边的两个图。我们现在定义两个电影类型(features:剧情、动画),右上图的表(矩阵)给出了每个电影对应类型的程度(如:《我不是药神》更属于剧情片,不属于动画),右下图的表中的数字给出了每个人喜欢每种电影类型的程度(李四更喜欢剧情片,不喜欢动画)。
那么光给出这两个表(矩阵)有什么用呢?我们把右上表中的第二列(col=《我不是药神》)和第三列(col=《变形金刚4》)分别与右下表的第二列(col=李四)对应元素相乘后相加(即点乘),得到的结果分别是(55 + -40=25)和(-25 + 50=-10),这两个分数的物理意义分别是李四喜欢《我不是药神》和李四喜欢《变形金钢4》的程度,可以看出李四更喜欢《我不是药神》。那么我们把右上表的每列和右下表的每列各元素相乘后相加,是不是可以得到每个人喜欢每部片子的程度呢?这不就是我们左边Rating matirx图表示的意思嘛!
现在我们给一部新电影《环太平洋》,给定他的类型指标(剧情:-1,动画:4),我们想知道李四喜欢这部片的程度。仍然依据上面的方法(即:李四喜欢剧情片的程度5✖️《环太平洋》是剧情片的程度-1 ➕李四喜欢动画的程度0✖️《环太平洋》是动画的程度4 = -5)。好吧,结果看来李四不喜欢这部片。
但是我们现在只有用户评分的数据呀,相当于只有左边的那个稀疏矩阵怎么办?一个字,学!🎓
Math
我们把评分矩阵(Rating Matrix)计作V, \(V\in R^{n\times m}\),那么V的每一行\(V_{i}\)代表一个人的所有评分,每一列\(V_{j}\)代表某一部电影所有人的评分,\(V_{ij}\)代表某个人i对某部电影j的评分。对应电影推荐来说,V必定是稀疏的,因为电影数量(列的数目)是巨大的,V中必定有很多很多项为null。
我们接下来看这两个矩阵U(Users Features Matrix )和M(Movie Features Matrix)。U为用户对特征的偏好程度矩阵,M为电影对特征的拥有程度矩阵。\(U\in R^{f\times n}\)的每一行表示用户,每一列表示一个特征,它们的值表示用户与某一特征的相关性,值越大,表明特征越明显。矩阵\(M\in R^{f\times m}\),的每一行表示电影,每一列表示电影与特征的关联。
那么U和M怎么得到呢?🤔️
还记得SVD的公式嘛?\(V=UM^{T}\),其实公式右边的中间还有个对角矩阵S,我们可以把他看成跟U相乘合并(The S matrix is left blended into the feature vectors, so only U and M remain)。其实,U和M这两个矩阵是通过学习的方式得到的,而不是直接做矩阵分解。我们定义如下的损失函数:
\(E = \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{m}I_{ij}(V_{ij} - p(U_i,M_j))^2+\frac{k_u}{2}\sum_{i=1}^{n}\lVert U_i \rVert^2 + \frac{k_m}{2}\sum_{j=1}^{m}\lVert M_j \rVert^2 \tag{1}\)
这里的评价指标metric采用的是RMSE。其中\(p(U_i,M_j)\)代表用户i对电影j的预测,最常用的预测函数p就是点乘,即 \(p(U_i,M_j)=U_{i}^{T}M_{j}\)。式(1)中的 \(I\in \{0,1\}^{n\times m}\),为一个指示器,指示相应位置是否有评分,有评分为1,没有为0。等式右边最后两项是正则化项,防止过拟合,这里不过多展开。
到这里,已经变成了一个机器学习的常见问题了,即最小化损失函数,用得最多的优化方法就是梯度下降,当然还有很多梯度下降的变体。下图是简单的梯度下降算法📖。

其中,\(\mu\)为学习率learning rate。且:
\(-\nabla _{U} =-\frac{\partial E}{\partial U_i} = \sum_{j=1}^{M}I_{ij}((V_{ij}-p(U_i,M_j))M_j) - k_uU_i \tag{2}\)
\(-\nabla _{M} =-\frac{\partial E}{\partial M_j} = \sum_{i=1}^{n}I_{ij}((V_{ij}-p(U_i,M_j))U_i) - k_mM_j \tag{3}\)
Improvements(adding bias)
可是,无奈的是🤷♂️,我们考虑这样一个事实:
有的人评价电影的时候喜欢打高分,比如我自己,在豆瓣上,就算很一般的电影我也会打3分左右,因为我貌似不是能做出打一分这种残忍的事的人😂。而有的人很严格,跟我正好相反。对于不同电影来说,比如姜文的《邪不压正》,我可能智商不高,实在觉得不好看,但是由于豆瓣评分颇高,为了掩饰我的看不懂,我还是打了4分。所以,分数这个事情有很强的主观性。即:
typical collaborative filtering data exhibits large systematic tendencies for some users to give higher ratings than others, and for some items to receive higher ratings than others.
所以,如果仅仅用 \(p(U_i,M_j)=U_{i}^{T}M_{j}\) 进行评分的预测就不那么明智了。在这里,我们考虑根据个人的口味和电影的级别来给予评分过程加一个偏置,即:(这里换一种形式:\(\mathbf{q}_i^T\mathbf{p}_u\)与\(U_{i}^{T}M_{j}\)等价)
\(\hat{r}_{ui} = \mu + b_i + b_u + \mathbf{q}_i^T\mathbf{p}_u \tag{4}\)
\(\mu\): 训练集中所有记录的评分的全局平均数。在不同网站中,因为网站定位和销售的物品不同,网站的整体评分分布也会显示出一些差异。比如有些网站中的用户就是喜欢打高分,而另一些网站的用户就是喜欢打低分。而全局平均数可以表示网站本身对用户评分的影响。
\(b_u\): 用户偏置(user bias)项。这一项表示了用户的评分习惯中和物品没有关系的那种因素。比如有些用户就是比较苛刻,对什么东西要求都很高,那么他的评分就会偏低,而有些用户比较宽容,对什么东西都觉得不错,那么他的评分就会偏高。
\(b_i\): 物品偏置(item bias)项。这一项表示了物品接受的评分中和用户没有什么关系的因素。比如有些物品本身质量就很高,因此获得的评分相对都比较高,而有些物品本身质量很差,因此获得的评分相对都会比较低。
有人就说了,这些偏置参数怎么定呢?难道我要预先把所有的数据集计算一遍?❌
才不需要呢,这些偏置参数也是通过学习而来,所以现在我们需要学习的矩阵参数变成了5个。😺
这个时候我们的损失函数变为:
\(E = \sum_{(u,i)\in \mathcal{k}}(r_{ui}-\mu - b_i - b_u - \mathbf{q}_i^T\mathbf{p}_u)^2 + \lambda (\lVert p_u \rVert^2 + \lVert q_i \rVert^2 + b_u^2 + b_i^2) \tag{5}\)
此时,我们的梯度下降也变成了这样:(\(\gamma\)为学习率)
\(b_u\leftarrow b_u + \gamma (e_{ui} - \lambda b_u) \tag{6}\)
\(b_i \leftarrow b_i + \gamma (e_{ui} - \lambda b_i \tag{7})\)
\(p_u \leftarrow p_u + \gamma (e_{ui} \cdot q_i - \lambda p_u) \tag{8}\)
\(q_i \leftarrow q_i + \gamma (e_{ui} \cdot p_u - \lambda q_i) \tag{9}\)
说到这里,SVD算法的本质是帮我们找到(学习出)item中隐含的维度(features),这些隐含的维度可以是(类型,派别,国别,或者两个组合,n种组合等等),SVD还可以找到(学习出)用户对各个维度(features)的类别喜爱程度。我们要做的只是指定维度的数量(n_factors),SVD会自动帮我们干好接下来的工作。
二、surprise
其实,当我知道要使用一个新库👖的时候,我是拒绝的。但是没办法,从头写代码实在是力不从心,把库中的代码先变成自己的再说是吧。下面先介绍surprise库的基本使用,然后重点分析里面的SVD算法。首先,import:
from surprise import SVD
from surprise import Dataset, Reader
from surprise.model_selection import cross_validate, train_test_split
1、初始化reader
制定评分范围为1-5,数据格式为四个
reader = Reader(rating_scale=(1, 5), line_format='user item rating timestamp')
2、初始化Dataset
传入的数据有四列。其实Reader和Dataset这两个类可以这样理解,前者为框架,定好各种参数,后者填入相应数据。
df_data = pd.read_csv('./data/ml-latest-small/ratings.csv', usecols=['userId','movieId','rating'])
data = Dataset.load_from_df(df_data, reader)
data
<surprise.dataset.DatasetAutoFolds at 0x1192bff60>
这里我们创建了一种新的类型 surprise.dataset,这已经不是pandas的dataframe,这样做的目的只是方便我们更好使用surprise的各种API。里面的数据格式是这样的:
elif df is not None:
self.df = df
self.raw_ratings = [(uid, iid, float(r) + self.reader.offset, None)
for (uid, iid, r) in self.df.itertuples(index=False)]
PS: 在查看源码的过程后,我发现surprise的load_from_df无法把dataframe里面的timestamp列包含进去。可能这是个bug?可以issue一下。
3、拆分data
trainset, testset = train_test_split(data, test_size=0.2) ### 实际调用 .split.ShuffleSplit()
trainset
<surprise.trainset.Trainset at 0x1131e6160>
4、训练模型
我们先来剖开surprise的SVD函数内部看看:
根据(4)式,定义p和q:
pu = rng.normal(self.init_mean, self.init_std_dev, (trainset.n_users, self.n_factors))
qi = rng.normal(self.init_mean, self.init_std_dev, (trainset.n_items, self.n_factors))
其中rng为np.random.RandomState(random_state),参数为随机数种子。
定义后,pu为一个n✖️f矩阵,qi为一个m✖️f矩阵
for current_epoch in range(self.n_epochs):
for u, i, r in trainset.all_ratings():
# 计算(5)的第一项
dot = 0 # <q_i, p_u>
for f in range(self.n_factors):
dot += qi[i, f] * pu[u, f]
err = r - (global_mean + bu[u] + bi[i] + dot)
# update biases
if self.biased:
# 根据式(6)
bu[u] += lr_bu * (err - reg_bu * bu[u])
# 根据式(7)
bi[i] += lr_bi * (err - reg_bi * bi[i])
# update factors
for f in range(self.n_factors):
puf = pu[u, f]
qif = qi[i, f]
# 根据式(8)
pu[u, f] += lr_pu * (err * qif - reg_pu * puf)
# 根据式(9)
qi[i, f] += lr_qi * (err * puf - reg_qi * qif)
好,现在开始训练模型,这里给定隐含的特征为30个。
model = SVD(n_factors=30)
model.fit(trainset)
<surprise.prediction_algorithms.matrix_factorization.SVD at 0x1138c1da0>
我们来看看模型生成的pu和qi矩阵,似乎很符合我们的要求。
print(model.pu.shape)
print(model.qi.shape)
(671, 30)
(8382, 30)
5、推荐
终于到推荐环节了,前面做的所有工作都是为了这一刻。 推荐也分为几种类型。一种是预测某个人对某部电影的评分,另一种是推荐给某个人新的几部电影。
这里我们预测userId为2对于movieId为14的评分:
model.predict(2,14)
Prediction(uid=2, iid=14, r_ui=None, est=3.3735354350374438, details={'was_impossible': False})
推荐电影可以用.get_neighbors()函数
Reference:
- https://surprise.readthedocs.io/en/stable/prediction_algorithms_package.html
- http://charleshm.github.io/2016/03/SVD-Recommendation-System/#fn:3
- https://juejin.im/post/5b1108bae51d4506c7666cac
- https://www.cnblogs.com/FengYan/archive/2012/05/06/2480664.html
文献:
- Ma C C. A Guide to Singular Value Decomposition for Collaborative Filtering[J]. 2008.
- Koren Y, Bell R, Volinsky C. Matrix Factorization Techniques for Recommender Systems[J]. Computer, 2009, 42(8):30-37.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号