机器学习笔记3
多变量线性回归
1.1 多维特征 Multiple features
继续以预测房屋价格为例,之前只有单变量,但在实际中是有多个变量(特征),比如除了房屋大小还有房间个数、房屋层数、房屋年限等
假设有m=47个样本

符号定义分别为:
n:特征的数量
x(i):第i个训练样本
xj(i):第i个训练样本中的第j个特征值
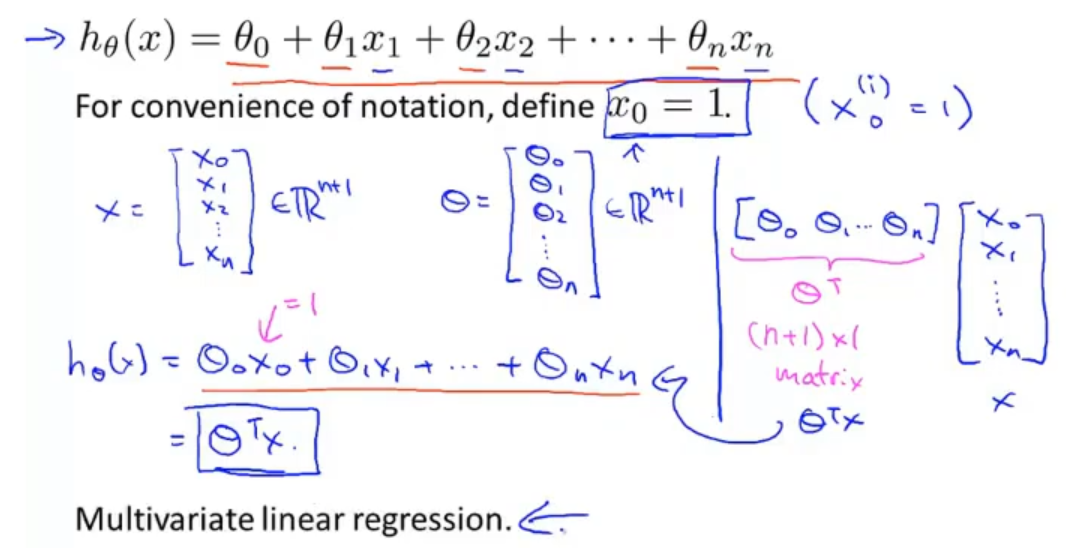
同时假设等式也相应得改变,不过这里可以巧妙的增加一个x0给θ0,这样就可以将整个假设等式转换为两个向量做内积
两个向量分别为列向量x和列向量θ,都是从0到n共有n+1个。这样原来的假设等式就转换为列向量θ的转置乘以列向量x。这种多特征的问题就相当于是多变量的线性回归问题
1.2 多变量的梯度下降 Gradient descent for multiple variables
1.2.1 多变量的梯度下降算法
在多变量的梯度下降中,参数θ不能再简单看成θ0,θ1...,θn,需要把参数看成一个n+1的向量θ
在代价函数中也不是简单的J(θ0,θ1...,θn),而是J(θ),同理在梯度下降中也是一样的,特别需要注意的是对J(θ)求偏导数

来看一下单变量和多变量梯度下降算法的比较,其实很多地方是很相似的

1.2.2 特征缩放
由于每个特征的数量级是不同的,比如房屋大小是在0-2000,而房见数量是在1-5,这样就会影响代价函数的等值线,从而导致梯度下降来回波动,效率低下
所以提出一个想法就是通过一种方法把不同的特征值映射到同一个数值范围内去,这样就会得到一个相对不错的代价函数的等值线
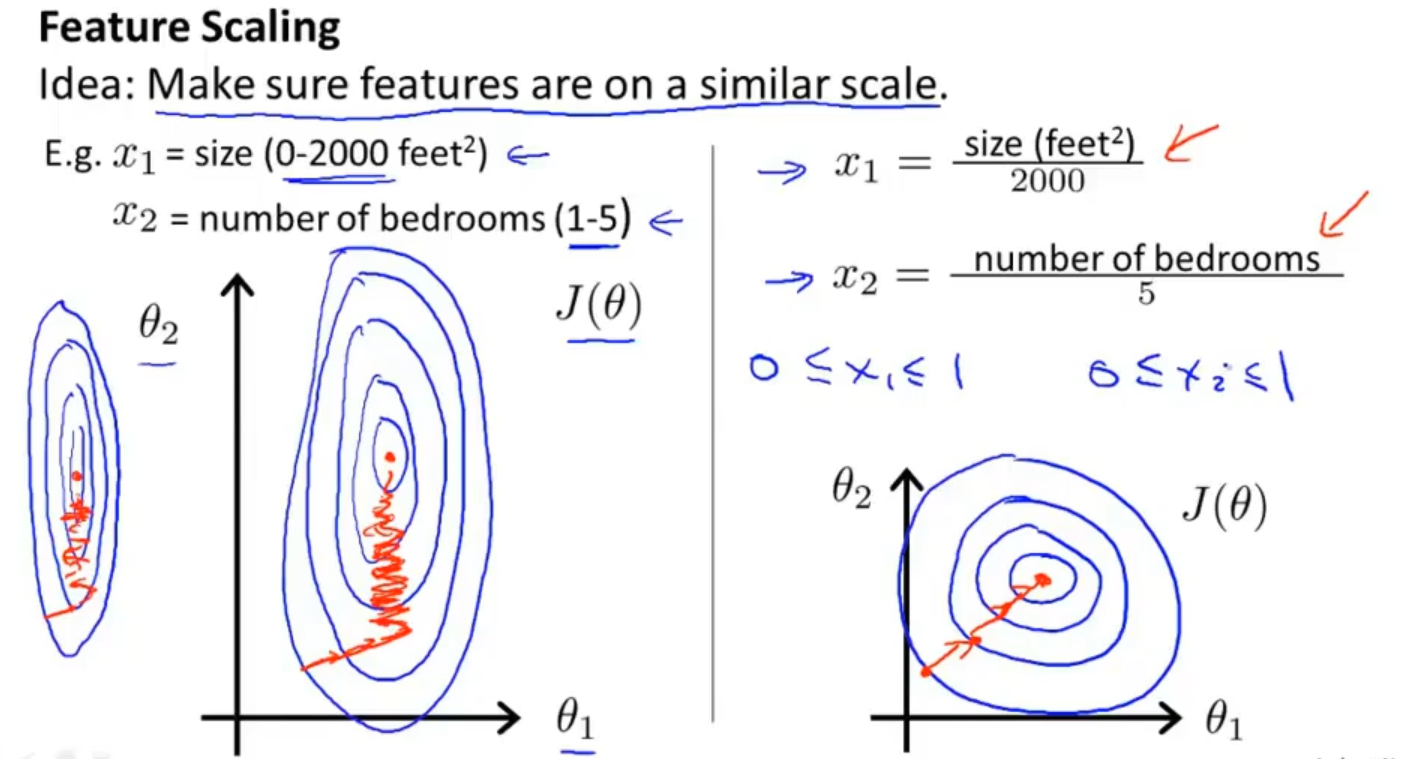
我们会选取一定范围的值来让每个特征值映射进来
但范围的选取也十分关键,不宜过大或者过小,这样就不能很好的表示特征了

我们也会使用均值归一化来使用特征缩放,均值归一化是让特征值减去平均值再除以最大值减去最小值或者是除以标准差 
以上就是特征缩放,通过简单的方法使梯度下降的速度更快,收敛所迭代的次数更少
1.2.3 学习率
确保梯度下降能够正常的运行,构建一个代价函数和迭代次数的图像,可以看出迭代到300到400次时代价函数已经逐渐收敛了,那我们就可以认为在迭代到400次时算法已经收敛
当然也可以使用自动的收敛测试来检测算法是否已经收敛,它是通过判断代价函数是否达到一个阈值来判断算法是否已经收敛的,但其实要选择一个合适的阈值也是比较困难的
相比较之下,还是左图比较直观

如果代价函数与迭代次数的图像遇到左边两种图这样的情况,就表明梯度下降不能正常的工作了,此时就需要使用较小的学习率α了
导致左图的原因通常都是使用了较大学习率α,这样情况就会导致右图代价函数中来回波动无法得到最小值,最后的结果越来越糟糕
但如果选择过于小的学习率α也会导致梯度下降的效率变得过低
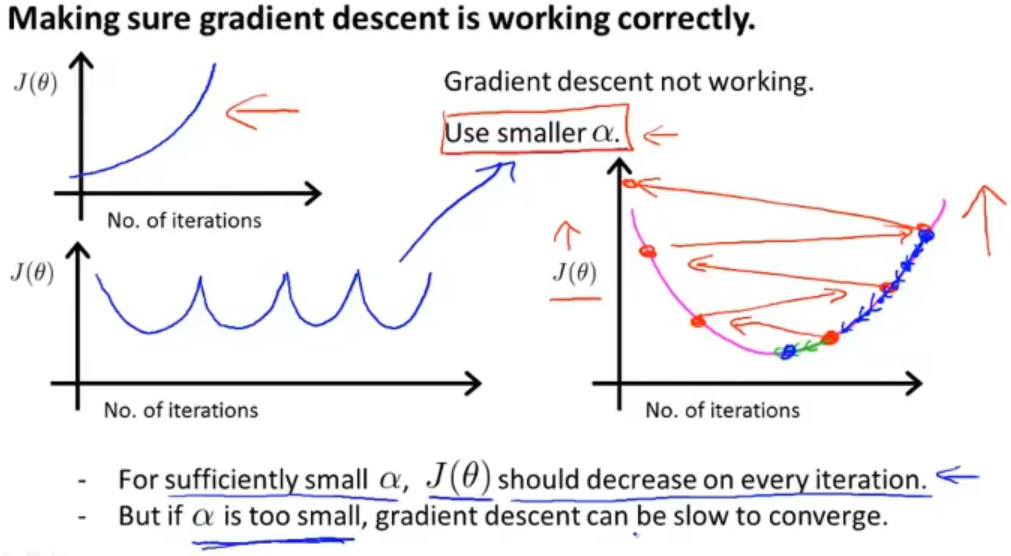

所以在选择学习率α的时候,我们可能会跨倍数(比如3倍)的去多尝试几个数值,这样就会得到一个不错的学习率
1.3 特征和多项式回归 Features and polynomial regression
1.3.1 特征
有时候通过定义一些新的特征可能会得到一个更好的模型,在预测房屋价格中,我们就可以不局限于房屋尺寸,可以定义的新的特征,比如:房屋尺寸的宽度和房屋尺寸的长度
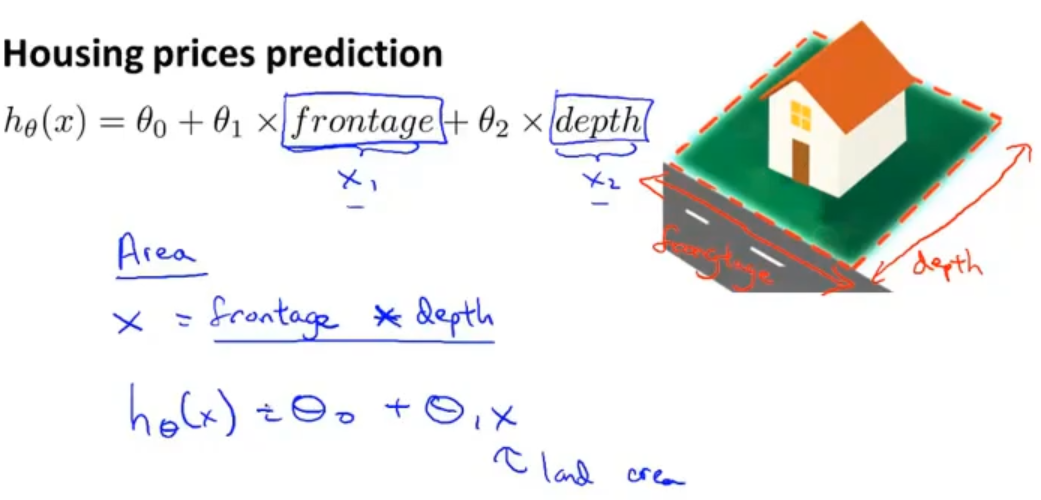
1.3.2 多项式回归
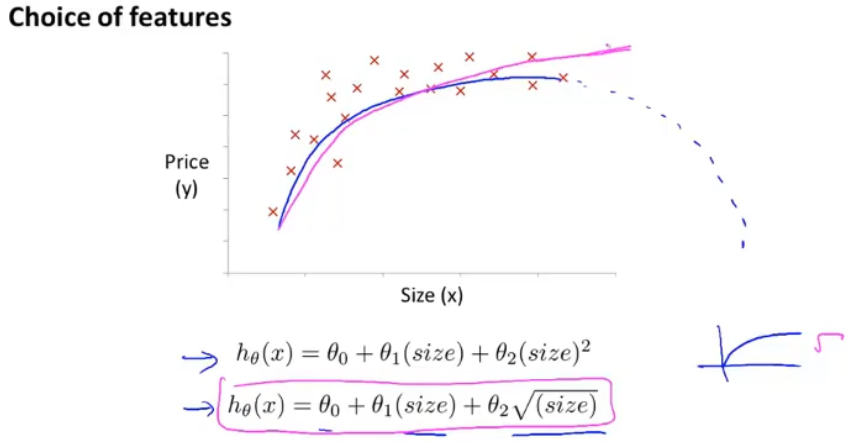
同样的思想可以运用在多项式中,在预测房屋价格中,不要局限于使用一次项的等式,可以扩展到二次项的等式,但是使用二次项的等式时,随着x的增大,y是从增大到减小的,与实际中的房屋不符
那么就可以考虑使用三次项的等式,在使用三次项的等式时,数量级会被扩大,在特征放缩时需要注意
同时在使用多项式时可以将不同次方的x看成一个变量,这样又把多项式回归转为多变量的线性回归

除了使用三次项的等式,还可以选择在原来的基础上加入平方根项的方式来使房价不下降
1.4 正规方程 Normal equation
在求解最优的θ过程中,除了使用梯度下降的迭代算法,还可以使用正规方程,正规方程可以不用迭代,一次性就把最优的θ求解出来 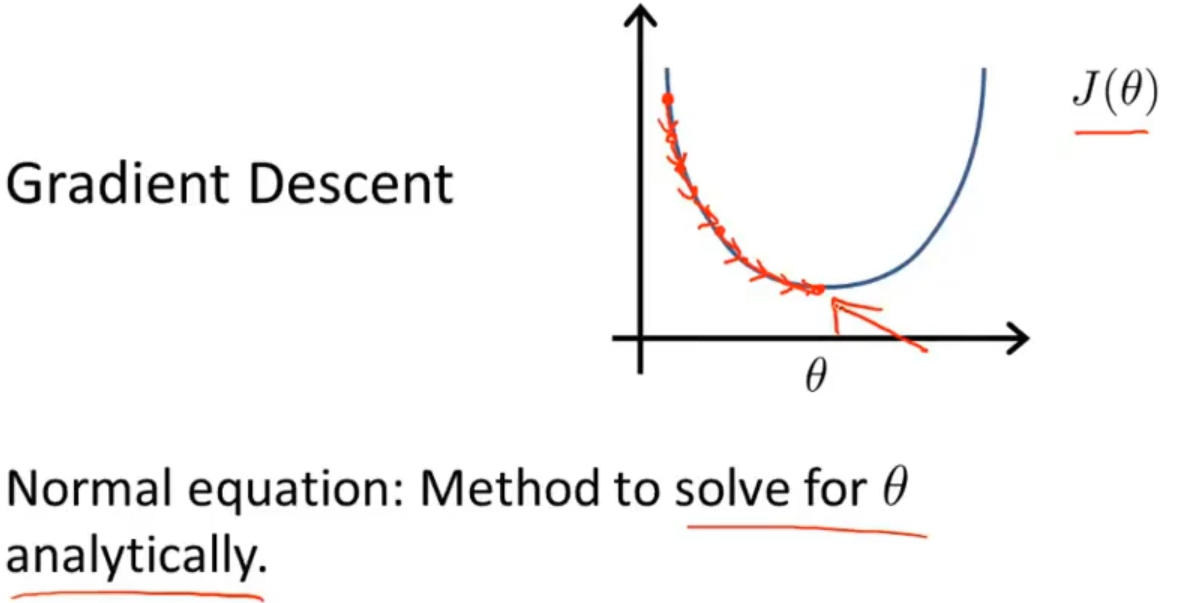
在一个简单的以θ为变量的例子中(如上半部分图)想要求解θ最小值是相对容易的,通过求导等于0就可以求解
但实际上我们需要求解的θ是一个向量,假设这个向量θ是n+1维的,如果我们从θ0到θn依次都使用求导等于0的办法求解最优参数θ就太麻烦了 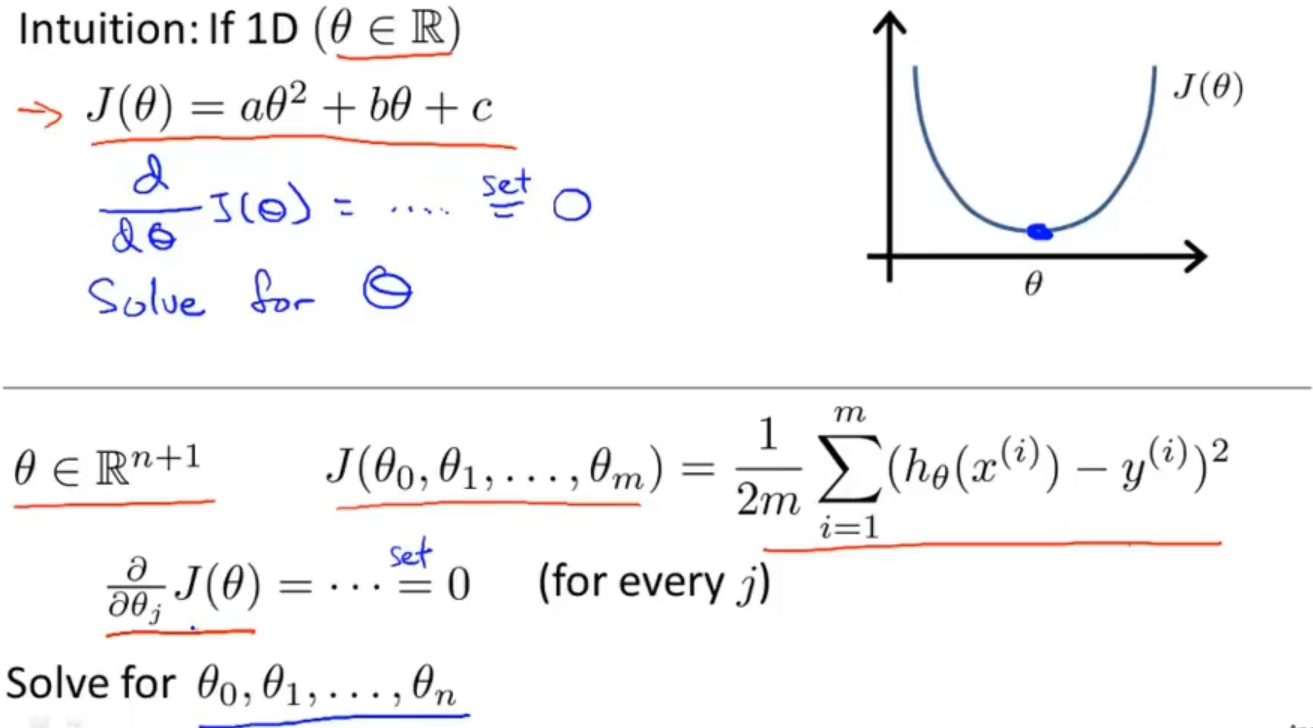
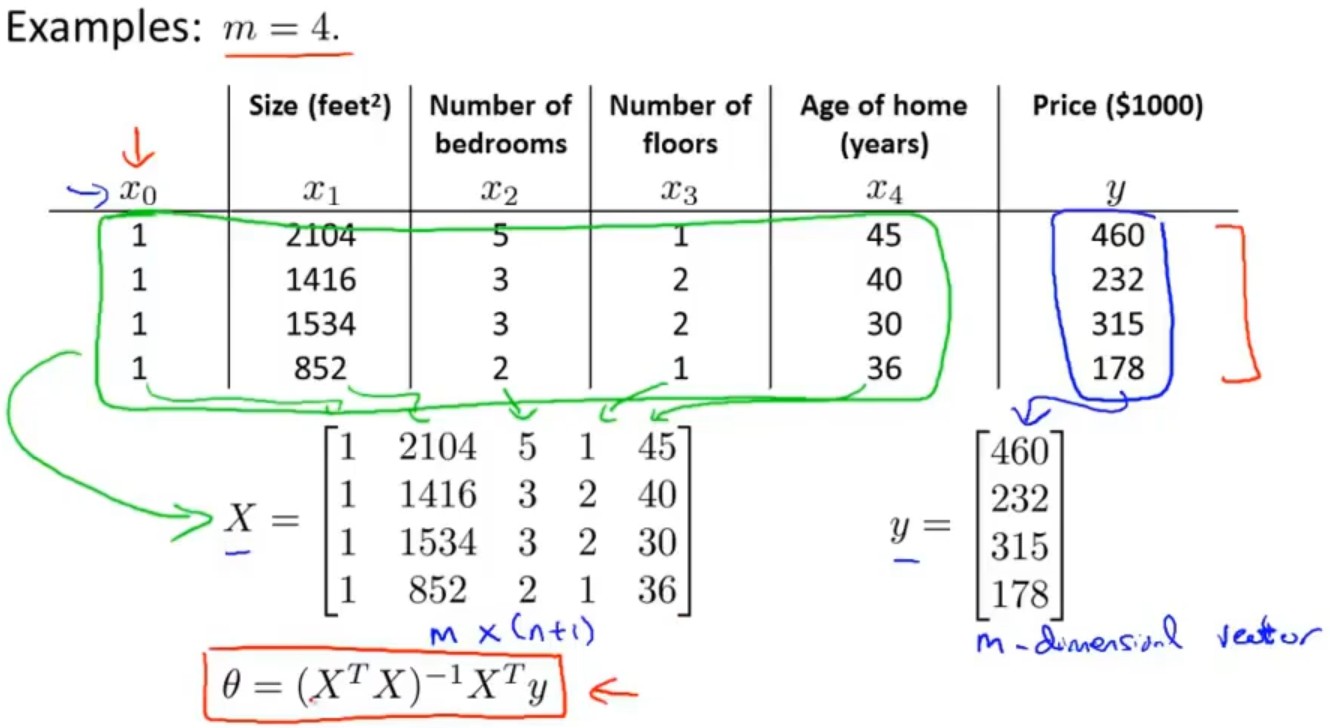
假设数据集中只有四个样本,将数据集中每个样本增加一个值为1的x0作为“特征”,把每个样本的特征值提取出来组成一个行向量,最后组成矩阵X,价格组成一个列向量y
通过计算 (XT*X)-1*XTy来得到最优的θ,关于公式的推导已经在数学上得到了证明
假设有m个样本,每个样本有n个特征,更一般化的理解如下图上半部分
下图下半部分是只考虑样本只有一个特征的情况
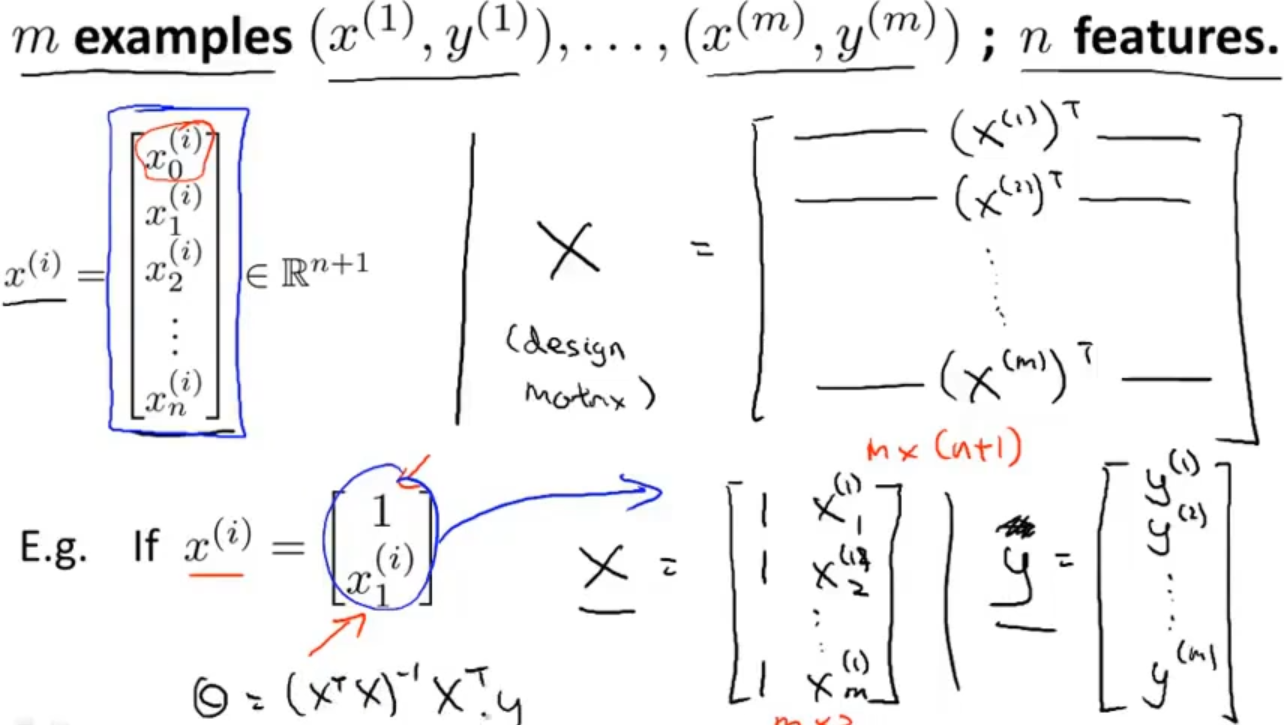
使用正规方程求解最优参数θ的时候可以不用考虑特征放缩
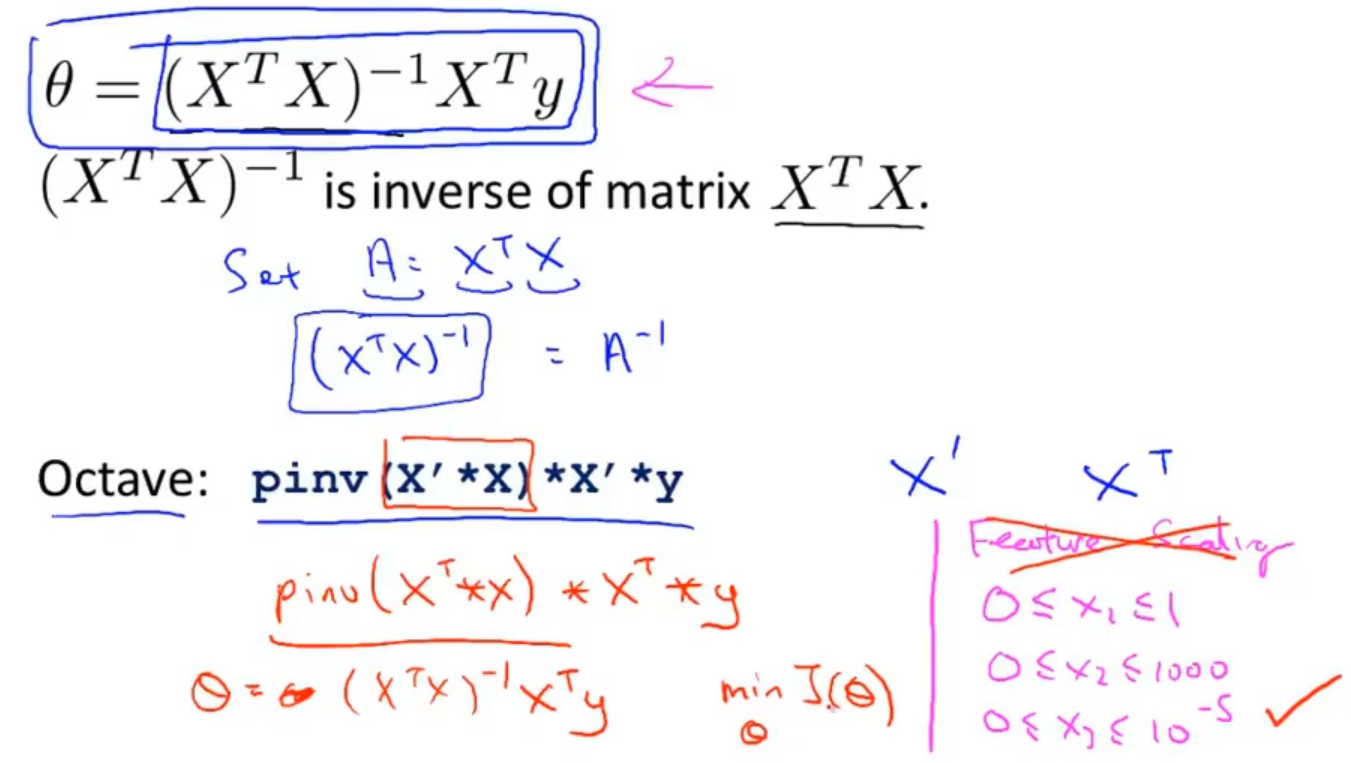
总结一下梯度下降算法和正规方程,梯度下降的的缺点就在于它需要去选择一个合适的学习率α,需要迭代许多次,这两个缺点正好是正规方程可以解决的,是正规方程的优点
当然在特征数n很大的时候,梯度下降是可以运行的比较好的,反而在正规方程中由于需要计算(XT*X)-1,时间复杂度至少是O(n3),当n非常大的时候,效率就很低了
那么到底n取多少才可以很好的区分使用哪个算法最优?其实并没有明确的定义,但通常认为当n超过10000时就会考虑使用梯度下降算法了 
举例:假设有(1, 1.3),(2.2, 2),(4, 4)三个点,利用正规方程在 Matlab中求得最优参数
x = [1 1;1 2.2;1 4]; y = [1.3;2;4]; w = (inv(x'*x))*x'*y;
求出参数
w =
0.2333
0.9167
展示效果
% 转变向量形式 x = [1 2.2 4]; y = [1.3 2 4]; z = 0:0.01:10; h = 0.9167*z + 0.2333; figure(1); plot(x,y,'*',z,h); xlim([0, 10]); ylim([0, 10])



 浙公网安备 33010602011771号
浙公网安备 33010602011771号