多元高斯分布（The Multivariate normal distribution）

在数据建模时，经常会用到多元高斯分布模型，下面就这个模型的公式并结合它的几何意义，来做一个直观上的讲解。

1， 标准高斯函数

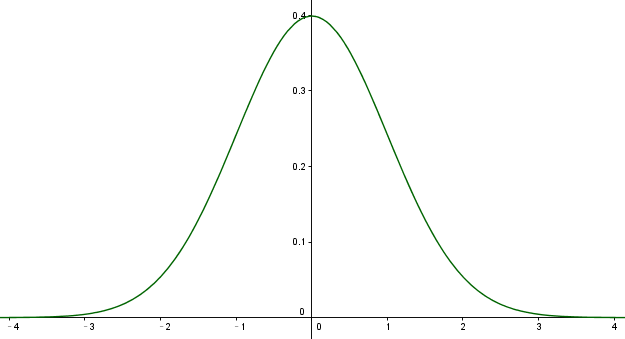
高斯函数标准型：

$f(x) = \frac{1}{\sqrt{2π}}e^{-\frac{x^2}{2}}$

这个函数描述了变量 x 的一种分布特性，变量x的分布有如下特点：

Ⅰ， 均值 = 0

Ⅱ， 方差为1

Ⅲ， 概率密度和为1

2， 一元高斯函数一般形式

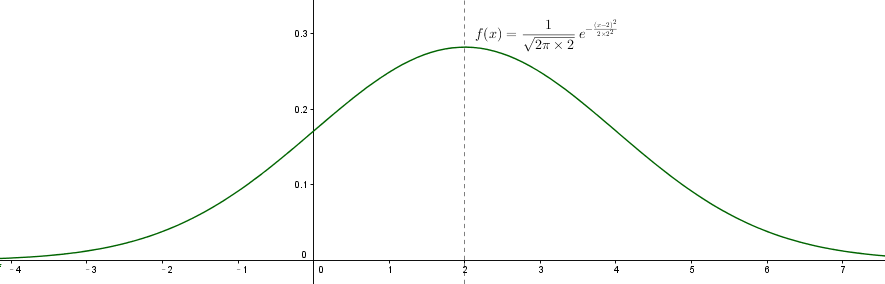
一元高斯函数一般形式：

$f(x) = \frac{1}{\sqrt{2π}σ}e^{-\frac{(x-μ)^2}{2σ^{2}}}$

我们可以令：

$z = \frac{x - μ}{σ}$

称这个过程为标准化， 不难理解，$z ∼ N(0, 1)$，从z -> x的过程如下：

Ⅰ， 将 x 向右移动 μ 个单位

Ⅱ， 将密度函数伸展 σ 倍

而标准化(x -> z)所做的事情就是上述步骤的逆向

唯一不太好理解的是前面 $\frac{1}{\sqrt{2π}σ}$ 中的σ， 为什么这里多了一个 σ， 不是 2σ 或其他？

当然，这里可以拿着概率密度函数的性质，使用微积分进行积分，为了保证最终的积分等于1， 这里必须是 σ

这里我想说一下自己的直观感受：

实线代表的函数是标准高斯函数：

$f(x) = \frac{1}{\sqrt{2π}}e^{-\frac{x^2}{2×2^{2}}}$

虚线代表的是标准高斯函数在 x 轴方向2倍延展，效果如下：

A(x = 1) -> D(x = 2)

E(x = 1.5) -> F(x = 3)

G(x = 2) -> H(x = 4)

横向拓宽了，纵向还是保持不变，可以想象，最后的函数积分肯定不等于1

采用极限的思想，将 x 轴切分成无穷个细小的片段，每个片段可以与函数围城一个区域，因为我的切分足够小，这个区域的面积可以近似采用公式：面积 = 底 × 高 求得：

从 AQRS -> DTUV， 底乘以2倍，高维持不变，所以，要保持变化前后面积不变，函数的高度应该变为原来的 1/2

所以高斯函数在 x 轴方向做2倍延展的同时，纵向应该压缩为原来的一半，才能重新形成新的高斯分布函数

扩展到一般情形，x 轴方向做 σ 倍延拓的同时， y 轴应该压缩 σ 倍（乘以 1/σ）

3, 独立多元正态分布

先假设n个变量 $x = \left[ \begin{matrix} x_{1}, x_{2},\cdots,x_{n}\end{matrix}\right]^\mathrm{T}$ 互不相关，且服从正态分布（维度不相关多元正态分布），各个维度的均值$E(x) = \left[ \begin{matrix} μ_{1}, μ_{2},\cdots,μ_{n}\end{matrix}\right]^\mathrm{T}$， 方差 $σ(x) = \left[ \begin{matrix} σ_{1}, σ_{2},\cdots,σ_{n}\end{matrix}\right]^\mathrm{T}$

根据联合概率密度公式：

$f(x) = p(x_{1},x_{2}....x_{n}) = p(x_{1})p(x_{2})....p(x_{n}) = \frac{1}{(\sqrt{2π})^nσ_{1}σ_{2}\cdotsσ_{n}}e^{-\frac{(x_{1}-μ_{1})^2}{2σ_{1}^2}-\frac{(x_{2}-μ_{2})^2}{2σ_{2}^2}\cdots-\frac{(x_{n}-μ_{n})^2}{2σ_{n}^2}}$

令 $z^{2} = \frac{(x_{1}-μ_{1})^2}{σ_{1}^2}+\frac{(x_{2}-μ_{2})^2}{σ_{2}^2}\cdots+\frac{(x_{n}-μ_{n})^2}{σ_{n}^2}$， $σ_{z}= σ_{1}σ_{2}\cdotsσ_{n}$

这样多元正态分布又可以写成一元那种漂亮的形式了(注意一元与多元的差别)：

$f(z) = \frac{1}{(\sqrt{2π})^nσ_{z}}e^{-\frac{z^2}{2}}$

因为多元正态分布有着很强的几何思想，单纯从代数的角度看待z很难看出z的概率分布规律，这里需要转换成矩阵形式：

$z^2 = z^\mathrm{T}z = \left[ \begin{matrix} x_{1} - μ_{1}, x_{2} - μ_{2}, \cdots,x_{n} - μ_{n}\end{matrix}\right] \left[ \begin{matrix} \frac{1}{σ_{1}^2}&0&\cdots&0\\
0&\frac{1}{σ_{2}^2}&\cdots&0\\
\vdots&\cdots&\cdots&\vdots\\
0&0&\cdots&\frac{1}{σ_{n}^2}
\end{matrix}\right]\left[ \begin{matrix} x_{1} - μ_{1}, x_{2} - μ_{2}, \cdots,x_{n} - μ_{n}\end{matrix}\right]^\mathrm{T}$

等式比较长，让我们要做一下变量替换：

$x - μ_{x} = \left[ \begin{matrix} x_{1} - μ_{1}, x_{2} - μ_{2}, \cdots,x_{n} - μ_{n}\end{matrix}\right]^\mathrm{T}$

定义一个符号

$∑_{}^{} = \left[ \begin{matrix} σ_{1}^2&0&\cdots&0\\
0&σ_{2}^2&\cdots&0\\
\vdots&\cdots&\cdots&\vdots\\
0&0&\cdots&σ_{n}^2
\end{matrix}\right]$

$∑_{}^{}$代表变量 X 的协方差矩阵， i行j列的元素值表示$x_{i}$与$x_{j}$的协方差

因为现在变量之间是相互独立的，所以只有对角线上 (i = j)存在元素，其他地方都等于0，且$x_{i}$与它本身的协方差就等于方差

$∑_{}^{}$是一个对角阵，根据对角矩阵的性质，它的逆矩阵：

$( (∑_{}^{})^{-1} = \left[ \begin{matrix} \frac{1}{σ_{1}^2}&0&\cdots&0\\
0&\frac{1}{σ_{2}^2}&\cdots&0\\
\vdots&\cdots&\cdots&\vdots\\
0&0&\cdots&\frac{1}{σ_{n}^2}
\end{matrix}\right]$

对角矩阵的行列式 = 对角元素的乘积

$σ_{z}= \left|∑_{}^{}\right|^\frac{1}{2} =σ_{1}σ_{2}.....σ_{n}$

替换变量之后，等式可以简化为：

$z^\mathrm{T}z = (x - μ_{x})^\mathrm{T}  \sum_{}{}^{-1} (x - μ_{x})$

代入以z为自变量的标准高斯分布函数中：

$f(z) = \frac{1}{(\sqrt{2π})^nσ_{z}}e^{-\frac{z^2}{2}} = \frac{1}{(\sqrt{2π})^{n}\left|∑_{}^{}\right|^\frac{1}{2}}e^{-\frac{ (x\  -\  μ_{x})^\mathrm{T}\  (\sum_{}{})^{-1}\  (x\  -\  μ_{x})}{2}}$ 

注意前面的系数变化：从非标准正态分布->标准正态分布需要将概率密度函数的高度压缩 $|∑_{}^{}|^\frac{1}{2}$倍， 从一维 -> n维的过程中，每增加一维，高度将压缩 $\sqrt{2π}$倍

维度不相关正太分布函数图像类似这样（以二元分布函数为例）：

4, 相关多元正态分布

前面也说了，我们讨论多元正态分布的前提是多元变量之间是相互独立的，实际上，有很多应用场合，变量与变量之间是有关联的。以二元正态分布为例：

                  

向输入平面作投影后的平面图：

以现在的坐标系来看，X1，X2是相关的，但是如果我们换一个角度，它们就是互不相关的了：

上述过程被称为去相关性，更专业一点叫做归化

假设新坐标系 $x_{1}' = \left[\begin{matrix}u_{x1}^{0}, u_{x1}^{1}\end{matrix}\right]^T$， $x_{2}' = \left[\begin{matrix}u_{x2}^{0}, u_{x2}^{1}\end{matrix}\right]^T$那么原坐标系上的任意一点 $[x_{1}, x_{2}]^T$ 投影到新坐标系上的结果为：

$\left[\begin{matrix}x_{1}'\\
x_{2}'\end{matrix}\right] = \left[ \begin{matrix} u_{x1}^{0}, u_{x1}^{1}\\
u_{x2}^{0}, u_{x2}^{1} \end{matrix} \right]\left[ \begin{matrix} x_{1}\\
x_{2} \end{matrix} \right]$

为了简单起见，定义矩阵：

$U = \left[ \begin{matrix} u_{x1}^{0}, u_{x2}^{0}\\
u_{x1}^{1}, u_{x2}^{1} \end{matrix} \right]$

U的列空间由新坐标向量组成，坐标映射之后：

$X’ = U^{T}X$

现在我们的自变量X’是相互独立的了，满足维度不相关高斯分布模型，现在我们想套用公式：

$f(z) = \frac{1}{(\sqrt{2π})^nσ_{z}}e^{-\frac{z^2}{2}} = \frac{1}{(\sqrt{2π})^{n}\left|∑_{}^{}\right|^\frac{1}{2}}e^{-\frac{ (x\  -\  μ_{x})^\mathrm{T}\  (\sum_{}{})^{-1}\  (x\  -\  μ_{x})}{2}}$ 

$x->x'$, 这个很容易，$μ_{x} -> μ(x')$这个也不难， 但是这里还有一个 $∑_{}^{}$是未知的！ 按照定义，这里的$∑_{}^{}$应该是X’的协方差，我们已知X，已知映射矩阵，如何求解X’的协方差？

从定义出发：

$μ_{x'} = E[U^TX] = U^TE[x] = U^Tμ_{x}$ $\tag{$1$}$

映射之后的协方差：

$\begin{align*}
σ(X') &= E[(X' - μ_{X'})(X' - μ_{X'})^T]\\
&=E[ (X' - μ_{X'}) (X'^T - μ_{X'}^T) ]\\
&=E[X'X'^T - μ_{X'}X'^T - X'μ_{X'}^T + μ_{X'}μ_{X'}^T]\\
&=E[U^TXX^TU-E[U^TX]X^TU - U^TXE[U^TX]^T + E[U^TX]E[U^TX]^T]\\
&=U^TE[XX^T - E(X)X^T - XE[X]^T + E[X]E[X]^T]U\\
&=U^Tσ(X)U\\
\end{align*}$

坐标映射前后的协方差矩阵满足关系：

$(\sum_{}^{})_{x'} = U^{T}(\sum_{}^{})_{x}U$ $\tag{$2$}$

再进一步观察，U的列向量是单位向量，而且是相互正交的，U是正交矩阵，$U^T = U^{-1}$

$(\sum_{}^{})_{x'} = U^{-1}(\sum_{}^{})_{x}U$ 

也就是说$(\sum_{}^{})_{x'}$ 是 $(\sum_{}^{})_{x}$的相似矩阵，相似矩阵的行列式相等

$|(\sum_{}^{})_{x'}| = |(\sum_{}^{})_{x}|$  $\tag{$3$}$

并且还有一个重要结论：

$(\sum_{}^{})_{x'}^{-1} = (U^T(\sum_{}^{})_{x}U)^{-1} =  (U^{-1}(\sum_{}^{})_{x}U)^{-1}=U^{-1}(\sum_{}^{})_{x}^{-1}U = U^{T}(\sum_{}^{})_{x}^{-1}U$ $\tag{$4$}$

有了上述1、2、3、4四个结论，我们就可以放心套用标准化公式了：

$\begin{align*}
f(z) &= \frac{1}{(\sqrt{2π})^nσ_{z}}e^{-\frac{z^2}{2}} \\
&= \frac{1}{(\sqrt{2π})^{n}\left|(∑_{}^{})'_{x}\right|^\frac{1}{2}}e^{-\frac{ (x'\ -\ μ_{x'})^\mathrm{T}\ (\sum_{}{})_{x'}^{-1}\ (x'\ -\ μ_{x'})}{2}}\\
&=\frac{1}{(\sqrt{2π})^{n}\left|(∑_{}^{})_{x}\right|^\frac{1}{2}}e^{-\frac{ (U^Tx\ -\ U^Tμ_{x})^\mathrm{T}\ U^T (\sum_{}{})_{x}^{-1}\ U (U^Tx\ -\ U^Tμ_{x})}{2}}\\
&=\frac{1}{(\sqrt{2π})^{n}\left|(∑_{}^{})_{x}\right|^\frac{1}{2}}e^{-\frac{ (x\ -\ μ_{x})^\mathrm{T}\ (\sum_{}{})_{x}^{-1}\ (x\ -\ μ_{x})}{2}}
\end{align*}$

 总结一下我们做了什么。

Ⅰ， 我们先定义了新的坐标系，通过矩阵 $U^{T}$ 将元素映射到新的坐标系，目的是去相关性

Ⅱ， 在新的坐标下，我们定义了新的期望、协方差、协方差的逆，他们都可以通过 $U$ 与 $U^T$计算出来，当然我们不用计算

Ⅲ,   套用标准公式，将新的期望、协方差的逆、协方差的行列式代入，发现最后的结果与$U$、$U^T$无关

为什么会这样？我的理解是这样：

前提条件：概率模型已经构建

假设空白平面上有一点A， 这个点A是客观存在的，一旦A指定了，那么它的概率大小P(A)就已经确定了

现在我们添加了一个坐标系，添加坐标系的好处只是使得P(A)可以被量化 $P(A) = f(u1, u2)$

同理，使用其他坐标系，可以得到其他坐标系下的另外一种量化 $P(A) = f(v1, v2)$

不管使用哪个坐标系，A点的概率始终是不变的，所以$f(u1, u2) = f(v1, v2)$（感觉这有点像哲学问题哈）。

5, 实例分析

$\sum_{}^{} = \left[ \begin{matrix} 1&0.8\\
0.8&1
\end{matrix} \right]$                     

这个图形与参数是如何对应的？

      

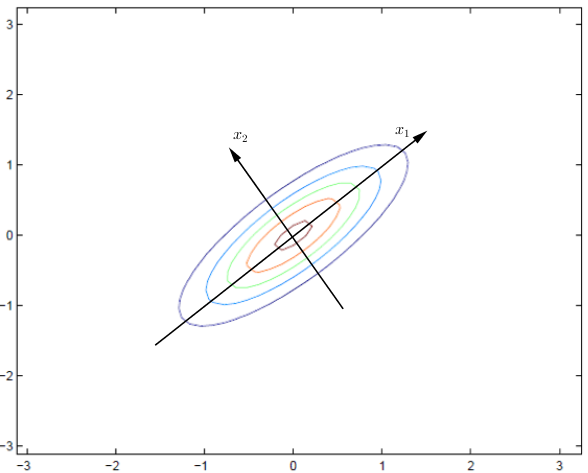
可以把那条假象的坐标轴线画出来，转换前后，坐标原点不变，很明显，这是一个旋转变换，假设坐标轴旋转的角度为θ，新的坐标向量矩阵将变为：

$U = \left[ \begin{matrix} cosθ&-sinθ\\
sinθ&cosθ
\end{matrix}\right]$

U的列空间组成了新坐标的坐标系

$U^T = \left[ \begin{matrix} cosθ&sinθ\\
-sinθ&cosθ
\end{matrix}\right]$

新坐标系下变量是不相关的，协方差矩阵为对角阵：

$(\sum_{}^{})_{new} = U^T \sum{} U = \left[ \begin{matrix} cosθ&sinθ\\
-sinθ&cosθ
\end{matrix}\right] \left[ \begin{matrix}
1&0.8\\
0.8&1
\end{matrix} \right] \left[ \begin{matrix} cosθ&-sinθ\\
sinθ&cosθ
\end{matrix}\right] = \left[ \begin{matrix} σ_{1}^2&0\\
0&σ_{2}^2
\end{matrix} \right]$

计算可得： $θ = \frac{π}{4}$ 

代入计算新的协方差为：

$(\sum_{}^{})_{new} = \left[ \begin{matrix} 1.8&0\\
0&0.2 \end{matrix} \right]$

得出的结论： 新的坐标系是原坐标系经过 $θ = \frac{π}{4}$旋转而来，在新的坐标系下，输入元素将会变得不相关，$x_{1}$方向的方差为1.8，分布比较宽， $x_{2}$方向的方差为0.2，分布比较窄，整体表现为扁平。

同理，不难得出：

               $\sum_{}^{} = \left[ \begin{matrix} 1&-0.5\\
-0.5&1
\end{matrix} \right]\qquad\qquad\qquad\qquad\sum_{}^{} = \left[ \begin{matrix} 1&-0.8\\
-0.8&1
\end{matrix} \right]\qquad\qquad\qquad\qquad\sum_{}^{} = \left[ \begin{matrix} 3&0.8\\
0.8&1
\end{matrix} \right]$                                                                           

 --------------------------------------------------------------------------------------------------------------------------------------------------------------------------

                                                                                                                                                                                路漫漫其修远兮，吾将上下而求索