输入一个非负数,判断二进制下该数含有“1”的个数。
一般解法
思路:依次检查每一位是否有为1,将数的每一位与1进行位与运算,若位运算结果为1则计数器加一。
int count_1(int num) {
if (!num) return 0;
int count = 0;//计数器
for (int i = 0; i < 32; ++i) {
if ((num >> i) & 1)
count++;
}
return count;
}
一次遍历,时间复杂度O(N),使用了常数空间,空间复杂度O(1)
进阶解法
二进制数若存在1, 对其进行减一操作,会发生以下变化:
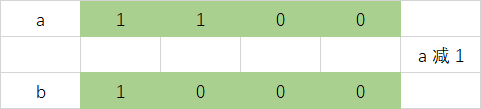
此时后面的数都会变为0,我们尝试计算 a&b:
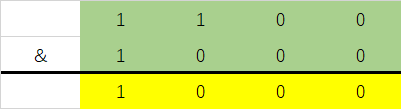
得到的是a失去一个1之后的结果,用这种方式我们能更快的计算出该数中含有1的个数:
int count_1(int num) {
int count = 0;
while (num) {
num = (num) & (num - 1);
count++;
}
return count;
}
时间复杂度O(M),M为实际含有1的个数,空间复杂度O(1) 。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号