【题解】[ABC276E] Round Trip

题面传送门

解决思路

首先得出一个结论：要有一条长度 \(\ge 4\) 的，起点终点相同的路径，这一条件等同于起点的上下左右四个点中，有任意两个是联通的。

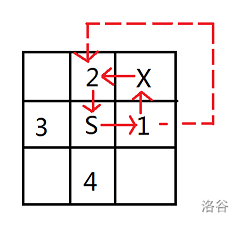
如图，以 \(1,2\) 两点为例，若他们是联通的，最差情况也是 \(S\to 1\to X\to 2\to S\)，长度为 \(4\)，满足要求。若 \(X\) 有障碍，则路径会变得更长。

所以题目就转化为了求 \(1,2,3,4\) 是否有任意两个点联通，只需从四个点分别开始 \(\text{BFS}\) 染色即可。

AC Code

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0)
#define int long long
using namespace std;
int n,m,sx,sy,tot=1;
int X[4]={0,0,1,-1},Y[4]={1,-1,0,0};
char c;
struct node{
	int x,y;
};
queue<node> q;
signed main(){
	IOS;TIE;
	cin>>n>>m;
	int vis[n+5][m+5];
	memset(vis,0,sizeof(vis));
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>c;
			if(c=='#') vis[i][j]=1;
			if(c=='S') sx=i,sy=j,vis[i][j]=1;
		}
	}
	for(int i=0;i<4;i++){
		int x=sx+X[i],y=sy+Y[i];
		if(x<1||x>n||y<1||y>m) continue;
		if(!vis[x][y]){
			tot++;
			vis[x][y]=tot;
			while(q.size()) q.pop();
			q.push({x,y});
			while(q.size()){
				node k=q.front();q.pop();
				for(int j=0;j<4;j++){
					int xx=k.x+X[j],yy=k.y+Y[j];
					if(xx<1||xx>n||yy<1||yy>m||vis[xx][yy]) continue;
					vis[xx][yy]=tot;
					q.push({xx,yy});
				}
			}
		}
		else if(vis[x][y]!=1){
			cout<<"Yes"<<endl;
			return 0;
		}
	}
	cout<<"No"<<endl;
	return 0;
}