理解深度学习:神经网络的双胞胎兄弟-自编码器(上)
前言
本篇文章可作为<利用变分自编码器实现深度换脸(DeepFake)>的知识铺垫。
自编码器是什么,自编码器是个神奇的东西,可以提取数据中的深层次的特征。
例如我们输入图像,自编码器可以将这个图像上“人脸”的特征进行提取(编码过程),这个特征就保存为自编码器的潜变量,例如这张人脸的肤色以及头发颜色,自编码器在提取出这些特征之后还可以通过这些特征还原我们的原始数据。这个过程称作“解码”。
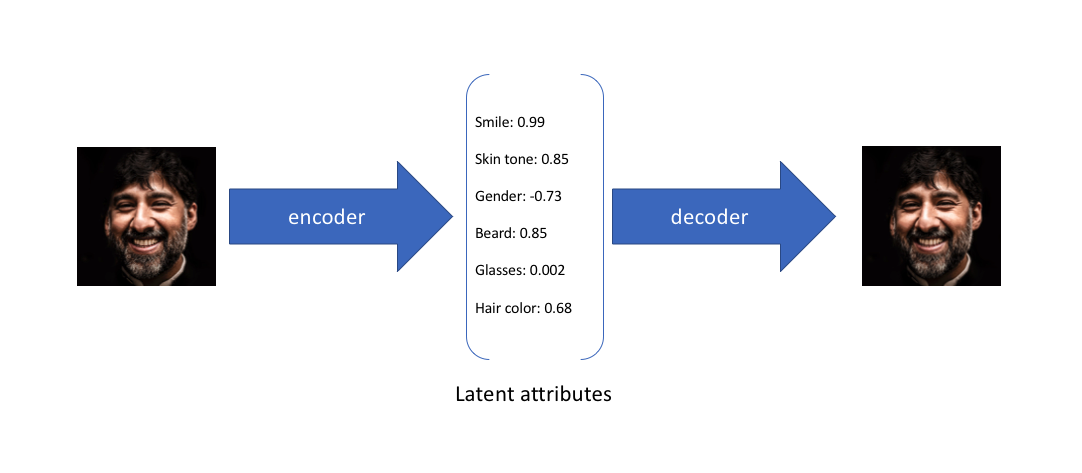
(以下相关图来自于jeremy)
自编码器其实也是神经网络的一种,神经网络我们都知道,我们设计好网络层,输入我们的数据,通过训练提供的数据进行前向操作提取特征,然后与准备好的标记进行比较,通过特定的损失函数来得到损失,然后进行反向操作实现对目标的分类和标定。
那么自编码器为什么说和神经网络很像呢?
什么是自编码器
自编码器也有自己的网络层,在自编码器中通常称之为隐藏层$h$,一个自编码器通常包含两个部分,一个为$h=f(x)$表示的编码器,另一个是$s=g(h)$表示的解码器。也就是$s=g(f(x))$。
当然编码器不可能输入$x$输出$x$,那样就太没意思了,编码器的主要特点是吸收输入数据的“特点”,然后再释放出来,可以理解为随机映射$p_{encoder}(h|x)$和$p_{decoder}(x|h)$。
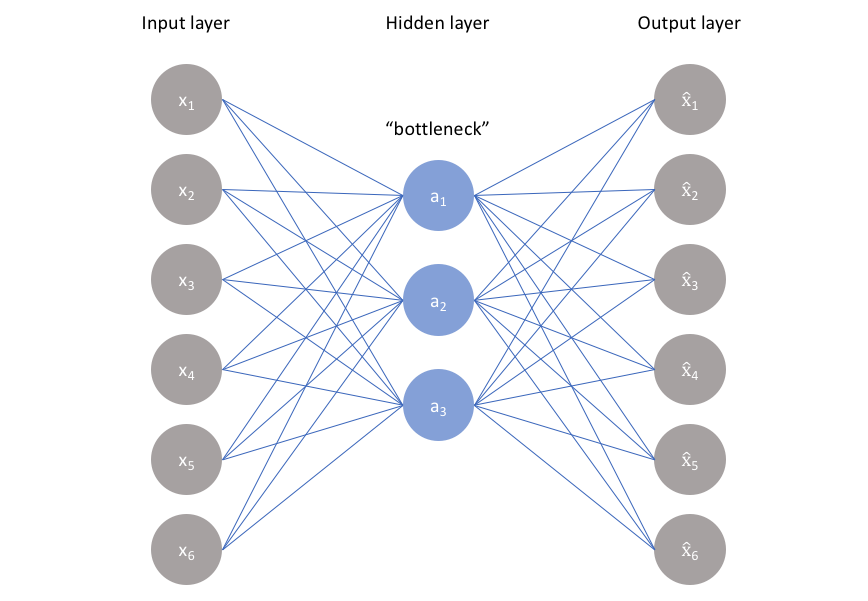
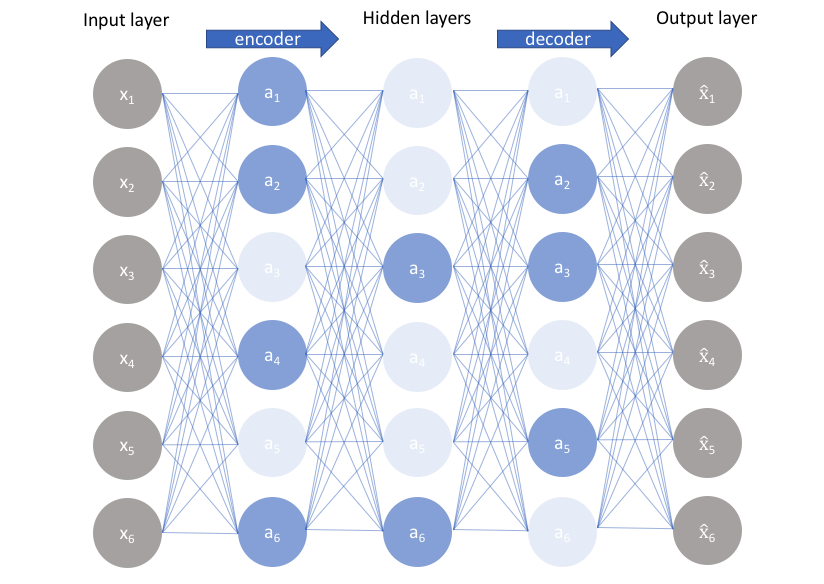
如上图(来自Jeremyjordan),我们可以看到输入input layer和output layer的维数是一样的,而隐含层的维数较小,所以我们也将自编码器理解为降维的过程。
但是要注意,自编码器属于无监督学习,也就是说,不同于神经网络,自编码器不需要任何其他的数据,只需要对输入的特征进行提取即可,当然我们要添加一些额外的限制条件来“强迫”自编码器提取我们想要的东西。
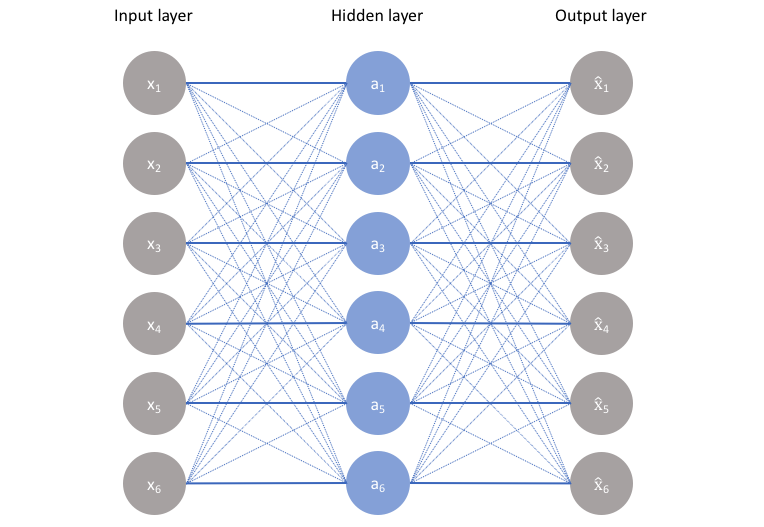
如果是上面这种网络的话,全是线性激活层,激活层可以记忆我们的输入,但也仅仅是记住了而已。在实际应用中,我们需要的隐含层应该可以很好地构建我们输入数据的信息,学习到我们的输入数据的一些分布和特点。
欠完备自编码器
自编码器我们想要它能够对输入的数据进行分析获取一些特性,而不是简单的输入输出,所以我们通过限制h的维度来实现,强迫自编码器去寻找训练数据中最显著的特征。
为什么叫欠完备,那是因为$h$的维度比输入$x$小。
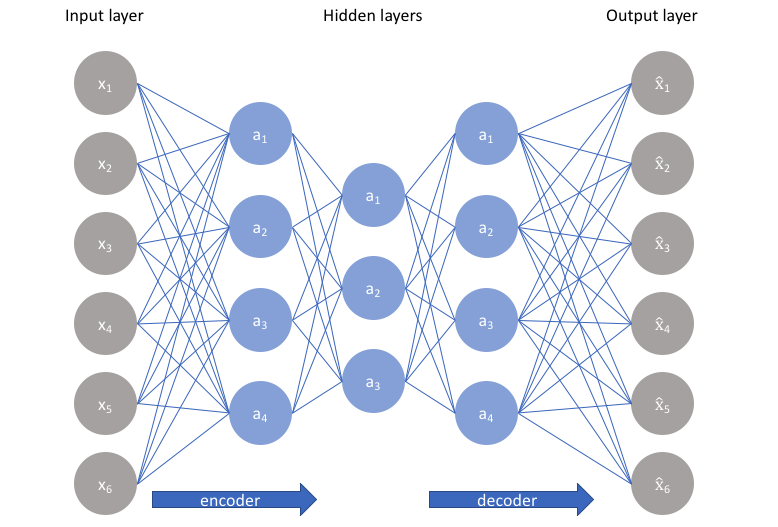
我们通过对输出设置一个损失函数(和神经网络中的损失函数相似):
$$L(x,g(f(x)))$$
然后通过减少损失(这个损失可以是均方误差等)来使$h$隐含层学习数据中最重要的信息。也就是学习数据中的潜在特性(Latent attributes)。
说白了这个自编码器和PCA(PCA是一个简单的机器学习算法,通过寻找矩阵中最大的特征向量来寻找输入数据的“特点”)很像。都是通过编码和解码来得到训练数据的隐含信息,但是如果这个隐含层是线性层(上图提到的)或者隐含层的容量很大,那么自编码器就无法学习到我们输入数据的有用信息。仅仅起一个复制的作用。
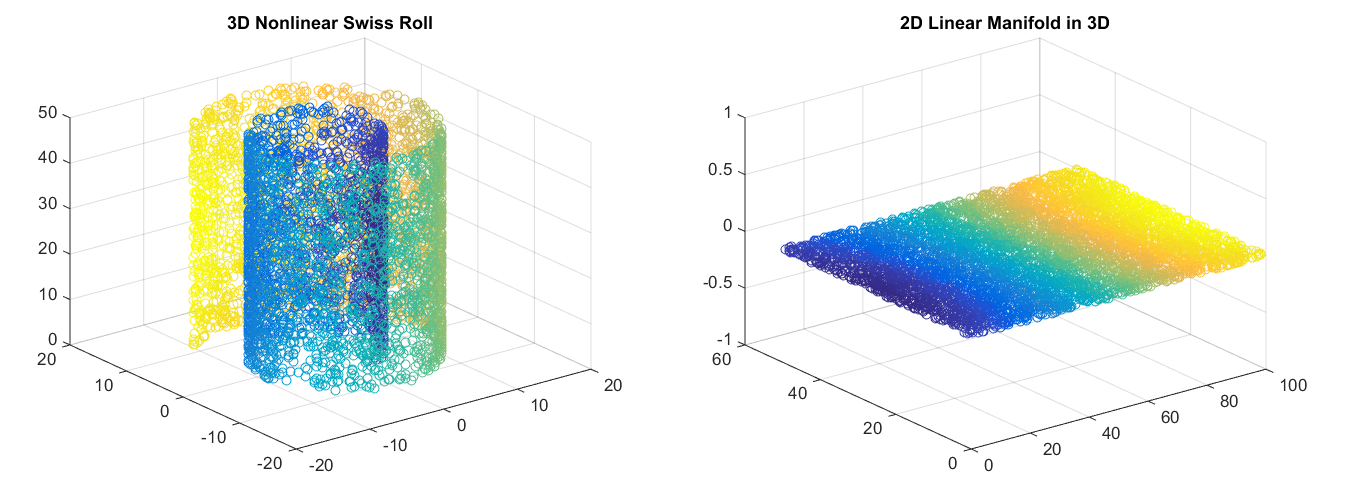
自编码器和PCA的不同在于自编码器可以学习到非线性特征,也就是通过非线性编码和非线性解码自编码器可以实现对数据的理解还原操作。对于高维的数据,自编码器就可以学习到一个复杂的数据表示(流形,manifold)。这些数据表示可以是二维的或者三维的形态(取决于我们自己的设置)。
为什么非线性的映射能够学到更多的东西,当然是因为非线性的表示能力更强,学习到的东西越多,从下图可以看出,对于二维空间中的一系列点,直线拟合(PCA)远远不如曲线拟合(自编码器)。
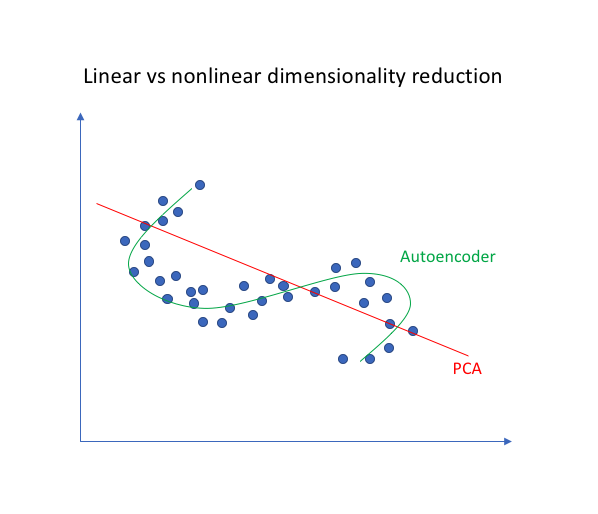
我们利用Pytorch(v0.4.0)简单编写一个程序来观察一下欠完备自编码器的效果:
首先我们设计一个基本的网络层(自编码器层),这里我们输入的数据是MNIST手写数据集,数据集的图像大小是28*28=784,所以我们设计的欠完备自编码器将我们的输入特征进行降维操作(我们输入的是$28 *28=784$维的数据),然后我们进行三次降维,将784维降到3维这样我们就可以将其进行可视化了。
下面自编码器层的设计:
class AutoEncoder(nn.Module):
def __init__(self):
super(AutoEncoder, self).__init__()
# 自编码器的编码器构造
self.encoder = nn.Sequential(
nn.Linear(28*28, 128), # 784 => 128
nn.LeakyReLU(0.1, inplace=True), # 激活层
nn.Linear(128, 64), # 128 => 64
nn.LeakyReLU(0.1, inplace=True),
nn.Linear(64, 12), # 64 => 12
nn.LeakyReLU(0.1, inplace=True),
nn.Linear(12, 3), # 最后我们得到3维的特征,之后我们在3维坐标中进行展示
)
# 自编码器的解码器构造
self.decoder = nn.Sequential(
nn.Linear(3, 12), # 3 => 12
nn.LeakyReLU(0.1, inplace=True),
nn.Linear(12, 64), # 12 => 64
nn.LeakyReLU(0.1, inplace=True),
nn.Linear(64, 128), # 64 -> 128
nn.LeakyReLU(0.1, inplace=True),
nn.Linear(128, 28*28), # 128 => 784
nn.Sigmoid(), # 压缩值的范围到0-1便于显示
)
def forward(self, x):
hidden = self.encoder(x) # 编码操作,得到hidden隐含特征
output = self.decoder(hidden) # 解码操作,通过隐含特征还原我们的原始图
return hidden, output
我们的优化器为:
optimizer = torch.optim.Adam(autoencoder.parameters(), lr=configure['lr'])
然后建立损失函数就可以进行训练了。
我们首先读取我们需要的数字图像集MNIST,然后将其投入我们设计的自编码器中进行训练,我们分别用原始输入图像和重构后的图像进行损失训练,通过降低损失我们就可以提取到数字数据集中的特征。最后,我们将我们提取的三维特征用三维坐标表示出来:
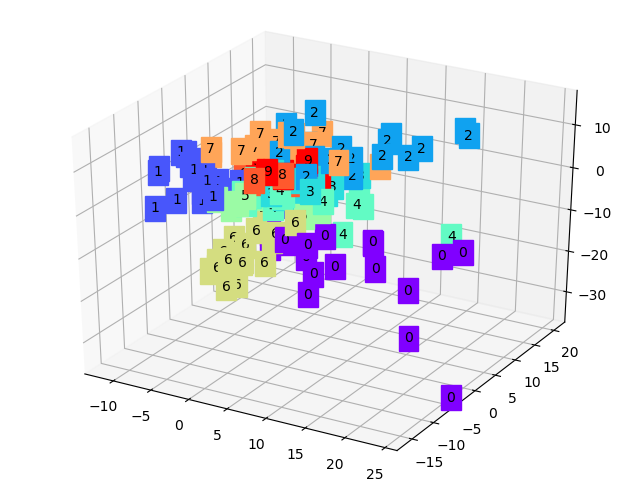
显然可以看到,每种数字(0-9)都有各自的特征簇,它们通常都聚在一起,换个角度再看一下:
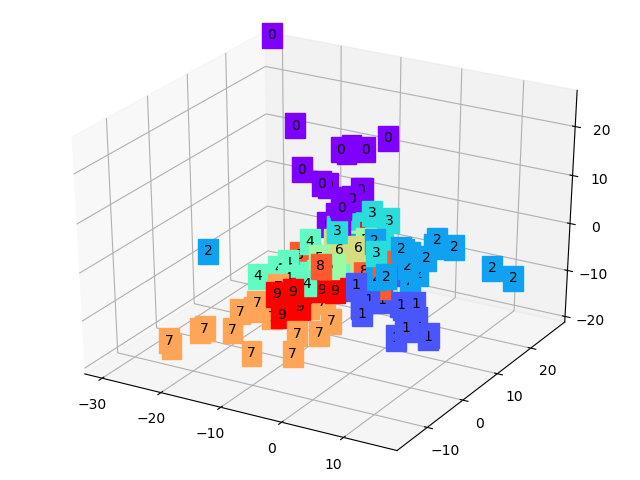
这样我们就把一些数字图从784维降到3维,将其提取到的特征通过三维坐标展示出来了。
我们也可以还原我们的输入数据(上一行是输入的图像,下一行是通过3维特征还原出来的),虽然还原的比较模糊,但是也可以看出我们正确提取了这些数字的特征。
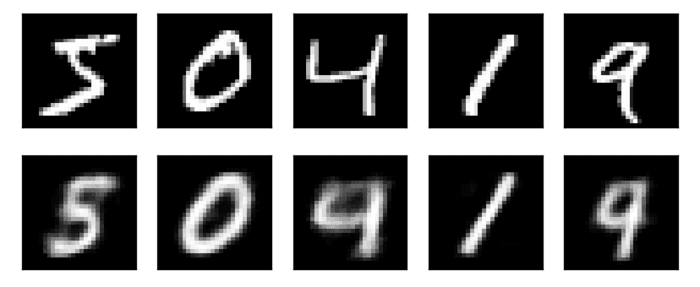
稀疏自编码器
稀疏自编码器是正则编码器的一种,正则即代表正则化,在之前的自编码器中我们的隐藏层的维数是小于输入层的,因此我们可以强迫自编码器学习数据的“特征”。但是,如果隐含层的维数和输入层的维数相同或者大于输入层的维数(也可以说是容量)。那么我们的自编码器可能就学不到什么有用的东西了。
这个时候应该怎么办,我们可以学习神经网络中经常用到的东西,那就是正则化。
稀疏编码器可以简单表示为:
$$L(x,g(f(x))) + \Omega(h)$$
其中$g(h)$表示解码器的输出,$h$是编码器的输出$h=f(x)$。
很简单,我们在损失函数的后面加了一项正则项,也可以称作惩罚项。结合一些神经网络的概念,我们可以将其理解为自编码器前馈网络中的正则项。
我们一般使用的正则项是L1正则损失,惩罚权重的绝对值,然后使用正则$\lambda$系数来调整。
$$ L(x,\hat x)+ \lambda\sum\limits_i|a_i^{(h)}| $$
另外一个常用的是$KL$散度,KL散度通常用来评价两个分布的关系,选择一个分布(通常是Bernoulli分布)然后将我们权重系数的分布与之进行比较,将其作为损失函数的一部分:
$$L(x,\hat x)+\sum\limits_{j}KL(\rho||\hat \rho_j)$$
其中$\rho$是我们选择要比较的分布,而$\hat \rho$表示我们权重系数的分布。
另外在《深度学习》中,有对稀疏编码器通过最大似然进行解释:


通过解释我们可以知道为什么通过加入正则项可以使隐含层学习到我们想要让学习到的东西。
还有个小问题,为什么叫稀疏自编码器,看下面的图就可以知道,隐含层中有些结点消失了,自然就变稀疏了。稀疏的隐含层与我们之前介绍的欠完备隐含层的区别是:稀疏自编码器可以使我们的隐含层中相对独立的结点对特定的输入特征或者属性变得更加敏感。 也就是说欠完备的自编码器的隐含层对输入数据所有的信息进行观测利用,而稀疏则不同,它是有选择性的,只对感兴趣的区域进行探测。
通过上面的稀疏策略我们可以保证在不牺牲网络对特征提取能力的同时,减少网络的容量,这样我们就可以挑输入信息中的特定信息去提取。
我们再通过Pytorch编程序来演示一下,我们修改自编码器的隐含层,将隐含层改成为与输入数据相同的维数(784),这样如果进行训练的话...损失函数的损失值是不会下降的,我们根据稀疏自编码器的特点加上一个正则项(惩罚项),怎么加呢,其实对权重进行惩罚那就是权重衰减,我们在设计优化器的时候加上一句话就可以了:
# weight_decay为权重衰减系数,我们这里设置为1e-4
# 但这里的惩罚函数为L2
optimizer = torch.optim.Adam(autoencoder.parameters(), lr=configure['lr'], weight_decay=1e-4)
这样就相当于算上了对权重的正则项,然后是我们的自编码层,可以看到所有维数都是一样的。
class AutoEncoder(nn.Module):
def __init__(self):
super(AutoEncoder, self).__init__()
self.encoder = nn.Sequential(
nn.Linear(28*28, 28*28), # 现在所有隐含层的维数是一样的,没有缩小也没有放大
nn.LeakyReLU(0.1, inplace=True),
nn.Linear(28*28, 28*28),
nn.LeakyReLU(0.1, inplace=True),
nn.Linear(28*28, 28*28),
)
self.decoder = nn.Sequential(
nn.Linear(28*28, 28*28),
nn.LeakyReLU(0.1, inplace=True),
nn.Linear(28*28, 28*28),
nn.LeakyReLU(0.1, inplace=True),
nn.Linear(28*28, 28*28),
nn.Sigmoid(),
)
def forward(self, x):
hidden = self.encoder(x)
output = self.decoder(hidden)
return hidden, output
当然我们也可以通过dropout来实现对权重的惩罚,这里就不演示了,我们对上面的自编码器进行训练得到的结果,然后对数字5的图像进行重构:
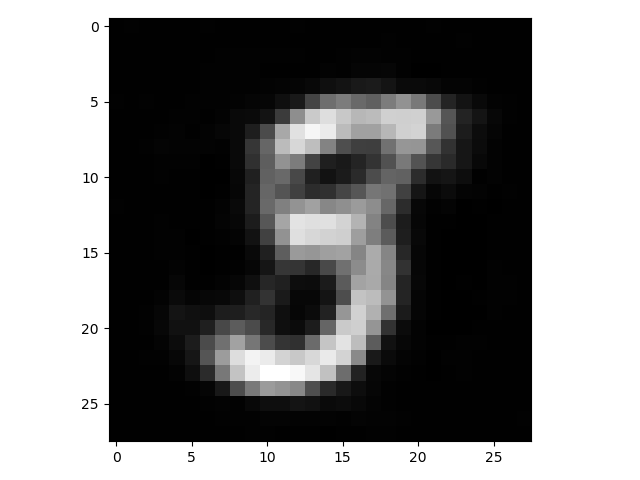
好吧,效果没有之前那个好,可能是正则化系数(权重衰减系数)需要调一下,但这个简单的例子也足以说明我们可以通过正则化来使隐含层学习我们想要学习的东西。
未完待续。
参考资料:
撩我吧
- 如果你与我志同道合于此,老潘很愿意与你交流;
- 如果你喜欢老潘的内容,欢迎关注和支持。
- 如果你喜欢我的文章,希望点赞👍 收藏 📁 评论 💬 三连一下~
想知道老潘是如何学习踩坑的,想与我交流问题~请关注公众号「oldpan博客」。
老潘也会整理一些自己的私藏,希望能帮助到大家,点击神秘传送门获取。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号