BP神经网络推导过程详解

      BP算法是一种最有效的多层神经网络学习方法，其主要特点是信号前向传递，而误差后向传播，通过不断调节网络权重值，使得网络的最终输出与期望输出尽可能接近，以达到训练的目的。

一、多层神经网络结构及其描述

    下图为一典型的多层神经网络。

  通常一个多层神经网络由L层神经元组成，其中：第1层称为输入层，最后一层（第L层）被称为输出层，其它各层均被称为隐含层（第2层~第L-1层）。

  令输入向量为：

\[ \vec x = [x_1 \quad x_2 \quad \ldots \quad x_i \quad \ldots \quad x_m], i=1,2,\ldots, m \]

   输出向量为：

\[ \vec y = [y_1 \quad y_2 \quad \ldots \quad y_k \quad \ldots \quad y_n], k = 1,2, \ldots,n \]

   第l隐含层各神经元的输出为：

\[ h^{(l)}= [h_1^{(l)} \quad h_2^{(l)} \quad \ldots \quad h_j^{(l)} \quad \ldots \quad h_{s_l}^{(l)}],j=1,2,\ldots,s_l \]

   其中，$s_l$为第l层神经元的个数。

   设$W_{ij}^{(l)}$为从l-1层第j个神经元与l层第i个神经元之间的连接权重；$b_i^{(l)}$为第l层第i个神经元的偏置，那么：

\[ h_i^{(l)} = f(net_i^{(l)})\]

\[ net_i^{(l)} = \sum_{j=1}^{s_{l-1}} W_{ij}^{(l)} h_j^{(l-1)} + b_i^{(l)}\]

      其中，$net_i^{(l)}$为l层第i个神经元的输入，$f(\cdot)$为神经元的激活函数。通常在多层神经网络中采用非线性激活函数，而不是用线性激活函数，因为采用基于线性激活函数的多层神经网络本质上还是多个线性函数的叠加，其结果仍然为一个线性函数。

二、激活函数

       BP神经网络通常使用下面两种非线性激活函数：

\[ f(x) = \frac 1 {1 + e^{-x}}\]

\[ f(x) = \frac {1 - e^{-x}} {1 + e^{-x}}\]

   第一种称为sigmod函数或者logistics函数，第二种为双曲正切函数。

       Sigmod函数的图像如下图所示，它的变化范围为(0, 1)，其导数为$f^{'} = f(1-f)$。

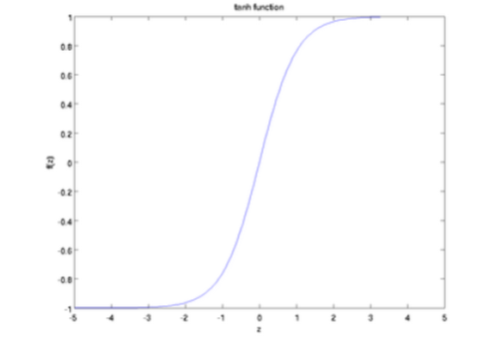
    双曲正切函数的图像如下图所示，它的变化范围为(-1, 1)，其导数为$f^{'} = 1-f^2$。

三、BP算法推导过程

   假定我们有m个训练样本$\{ (x(1), y(1)), (x(2), y(2)), \ldots, (x(m), y(m))\}$，其中$d(i)$为对应输入$x(i)$的期望输出。BP算法通过最优化各层神经元的输入权值以及偏置，使得神经网络的输出尽可能地接近期望输出，以达到训练（或者学习）的目的。

   采用批量更新方法，对于给定的m个训练样本，定义误差函数为：

\[ E = \frac 1 m \sum_{i=1}^m E(i) \]

        其中，E(i)为单个样本的训练误差：

\[ E(i) = \frac 1 2 \sum_{k=1}^n (d_k(i) - y_k(i))^2 \]

        因此，

\[ E = \frac 1 {2m} \sum_{i=1}^m \sum_{k=1}^n (d_k(i) - y_k(i))^2\]

       BP算法每一次迭代按照以下方式对权值以及偏置进行更新：

\[ W_{ij}^{(l)} = W_{ij}^{(l)} -\alpha \frac {\partial E} {\partial W_{ij}^{(l)}} \]

\[ b_i^{(l)} = b_i^{(l)} -\alpha \frac {\partial E} {\partial b_i^{(l)}}\]       

   其中，$\alpha$为学习速率，它的取值范围为(0, 1)。BP算法的关键在于如何求解$W_{ij}^{(l)}$和$b_i^{(l)}$的偏导数。

   对于单个训练样本，输出层的权值偏导数计算过程：

\begin{equation*}
\begin{split}
\frac {\partial E(i)} {\partial W_{kj}^{(L)}}&=\frac {\partial} {\partial W_{kj}^{(L)}} (\frac 1 2 \sum_{k=1}^n (d_k(i)-y_k(i))^2) \\
&=\frac {\partial} {\partial W_{kj}^{(L)}} (\frac 1 2 (d_k(i)-y_k(i))^2)\\
&=-(d_k(i)-y_k(i))\frac {\partial y_k(i)} {\partial W_{kj}^{(L)}}\\
&=-(d_k(i)-y_k(i))\frac {\partial y_k(i)} {\partial net_k^{(L)}} \frac {\partial net_k^{(L)}} {\partial W_{kj}^{(L)}}\\
&=-(d_k(i)-y_k(i))f(x)^{'}|_{x=net_k^{(L)}} \frac {\partial net_k^{(L)}} {\partial W_{kj}^{(L)}}\\
&=-(d_k(i)-y_k(i))f(x)^{'}|_{x=net_k^{(L)}} h_j^{(L-1)}
\end{split}
\end{equation*}

     即：

\[
\frac {\partial E(i)} {\partial W_{kj}^{(L)}} = -(d_k(i) - y_k(i))f(x)^{'}|_{x=net_k^{(L)}}h_j^{(L-1)}
\]

     同理可得，

 

\[
\frac {\partial E(i)} {\partial b_{k}^{(L)}} = -(d_k(i) - y_k(i))f(x)^{'}|_{x=net_k^{(L)}}
\]    

    令：

\[
\delta_k^{(L)} = -(d_k(i) - y_k(i))f(x)^{'}|_{x=net_k^{(L)}}
\]    

    则：

\[
\frac {\partial E(i)} {\partial W_{kj}^{(L)}} = \delta_k^{(L)} h_j^{(L)}
\]

\[
\frac {\partial E(i)} {\partial b_{k}^{(L)}} = \delta_k^{(L)}
\]        

  对隐含层L-1层：

\begin{equation*}
\begin{split}
\frac {\partial E(i)} {\partial W_{ji}^{(L-1)}}&=\frac {\partial} {\partial W_{ji}^{(L-1)}} (\frac 1 2 \sum_{k=1}^n (d_k(i)-y_k(i))^2) \\
&=\frac {\partial} {\partial W_{ji}^{(L-1)}} (\frac 1 2 \sum_{k=1}^n (d_k(i)-f(\sum_{j=1}^{s_{L-1}} W_{kj}^{(L)} h_j^{(L-1)} + b_k^{(L)}))^2) \\
&=\frac {\partial} {\partial W_{ji}^{(L-1)}} (\frac 1 2 \sum_{k=1}^n (d_k(i)-f(\sum_{j=1}^{s_{L-1}} W_{kj}^{(L)} f(\sum_{i=1}^{s_{L-2}} W_{ji}^{(L-2)}h_i^{(L-2)} + b_j^{(L-1)}) + b_k^{(L)}))^2) \\
&=-\sum_{k=1}^n (d_k(i) - y_k(i)) f(x)^{'}|_{x=net_k^{(L)}} \frac {\partial net_k^{(L)}} {\partial W_{ji}^{(L-1)}}
\end{split}
\end{equation*}

  因为，

\begin{equation*}
\begin{split}
net_k^{(L)} &=\sum_{j=1}^{s_{L-1}} W_{kj}^{(L)} h_j^{(L-1)} + b_k^{(L)} \\
&=\sum_{j=1}^{s_{L-1}} W_{kj}^{(L)} f(\sum_{i=1}^{s_{L-2}} W_{ji}^{(L-2)}h_i^{(L-2)} + b_j^{(L-1)}) + b_k^{(L)} \\
&=\sum_{j=1}^{s_{L-1}} W_{kj}^{(L)} f(net_j^{(L-1)})
\end{split}
\end{equation*}

  所以，

\begin{equation*}
\begin{split}
\frac {\partial E(i)} {\partial W_{ji}^{(L-1)}}&= \sum_{k=1}^n (d_k(i) - y_k(i)) f(x)^{'}|_{x=net_k^{(L)}} \frac {\partial net_k^{(L)}} {\partial W_{ji}^{(L-1)}} \\
&= \sum_{k=1}^n (d_k(i) - y_k(i)) f(x)^{'}|_{x=net_k^{(L)}} \frac { \partial net_k^{(L)}} {\partial f(net_j^{(L-1)})} \frac {\partial f(net_j^{(L-1)})} {\partial net_j^{(L-1)}} \frac {\partial net_j^{(L-1)}} {\partial W_{ji}^{(L-1)}} \\
&= \sum_{k=1}^n (d_k(i) - y_k(i)) f(x)^{'}|_{x=net_k^{(L)}} W_{kj}^{(L)} f(x)^{'}|_{x = net_j^{(L-1)}} h_i^{(L-2)}
\end{split}
\end{equation*}

  同理，

\[
\frac {\partial E(i)} {\partial b_j^{(L-1)}} = \sum_{k=1}^n (d_k(i) - y_k(i)) f(x)^{'}|_{x=net_k^{(L)}} W_{kj}^{(L)} f(x)^{'}|_{x = net_j^{(L-1)}}
\]

  

  令：

\begin{equation*}
\begin{split}
\delta_j^{(L-1)} &= \sum_{k=1}^n (d_k(i) - y_k(i)) f(x)^{'}|_{x=net_k^{(L)}} W_{kj}^{(L)} f(x)^{'}|_{x = net_j^{(L-1)}} \\
&=\sum_{k=1}^n W_{kj}^{(L)} \delta_k^{(L)} f(x)^{'}|_{x = net_j^{(L-1)}}
\end{split}
\end{equation*}

\[
\frac {\partial E(i)} {\partial W_{ji}^{(L-1)}} = \delta_j^{(L-1)} h_i^{(L-2)}
\]

 

\[
\frac {\partial E(i)} {\partial b_j^{(L-1)}} = \delta_j^{(L-1)}
\]

  

  由上可推，第l层（$2 \leq l \leq L-1 $）的权值和偏置的偏导可以表示为：

\[
\frac {\partial E(i)} {\partial W_{ji}^{(l)}} = \delta_j^{(l)} h_i^{(l-1)}
\]

\[
\frac {\partial E(i)} {\partial b_j^{(l)}} = \delta_j^{(l)}
\]

    其中，

\[
\delta_j^{(l)} = \sum_{k=1}^{s_{l+1}} W_{kj}^{(l+1)} \delta_k^{(l+1)} f(x)^{'}|_{x=net_{j}^{(l)}}
\]

四、BP算法过程描述

  采用批量更新方法对神经网络的权值和偏置进行更新：

1. 对所有的层$2 \leq l \leq L$，设$\Delta W^{(l)} = 0, \Delta b^{(l)} = 0 $，这里$\Delta W^{(l)} $和$\Delta b^{(l)} $分别为全零矩阵和全零向量；
2. For i = 1:m，
   1. 使用反向传播算法，计算各层神经元权值和偏置的梯度矩阵$\nabla W^{(l)} (i)$和向量和$\nabla b^{(l)}(i) $；
   2. 计算$\Delta W^{(l)} = \nabla W^{(l)}(i) $；
   3. 计算$\Delta b^{(l)} = \nabla b^{(l)}(i)$。
3. 更新权值和偏置：
   1. 计算$W^{(l)} = W^{(l)} + \frac 1 m \Delta W^{(l)} $；
   2. 计算$b^{(l)} = b^{(l)} + \frac 1 m \Delta b^{(l)} $。