理论基础 —— 线性表 —— 循环链表

【概述】

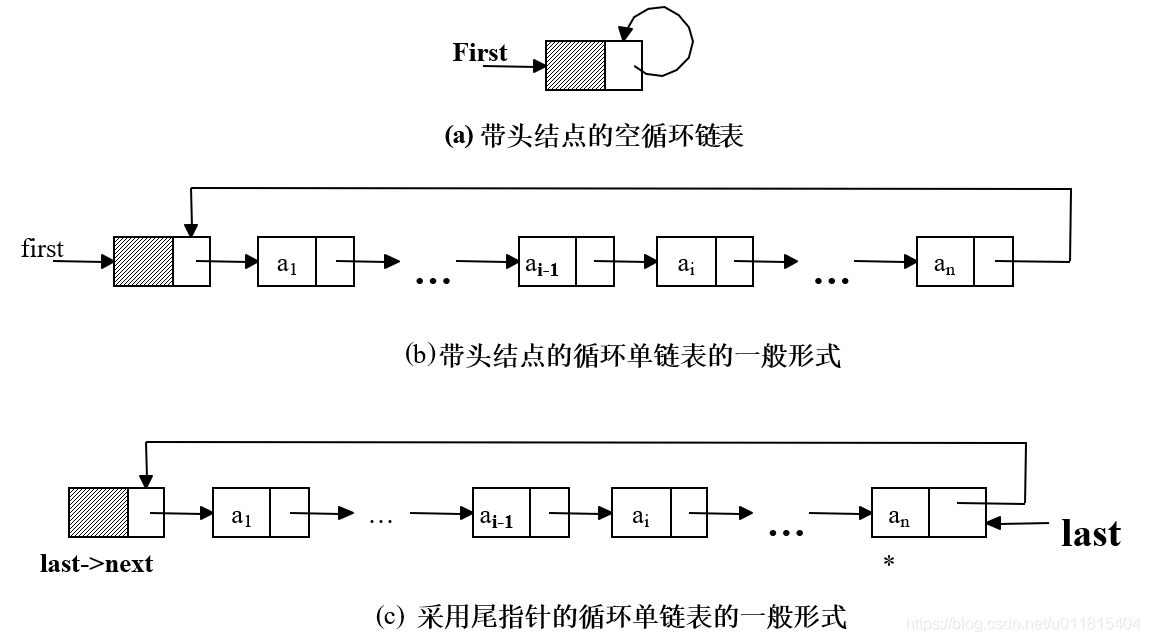
循环链表的构建与单链表十分相似，唯一不同的是，对于链表的表尾，需要将原来的 NULL 改为 first

以下仅给出构造函数的实现

【构造函数】

1.无参构造函数

生成一个头结点，让头指针指向头结点，并将头结点的指针域指向头指针。

template <class T>
linkList<T>::circleList(){//无参构造函数
    first=new Node<T>;//头指针指向头结点
    first->next=first;//头结点的指针域指向头指针
}

2.有参构造函数

1）头插法

使用头插法的有参构造函数，构造循环链表的主体部分与单链表一致，区别在于要在一开始令头结点指向头指针，即 first->next=first

template <class T>
linkList<T>::circleList(T a[],int n){//头插法的有参构造函数
    first=new Node<T>;
    first->next=first;//头结点指向头指针
 
    //与单链表一致
    for(int i=0;i<n;i++){
        Node<T> *s=new Node<T>;
        s->data=a[i];
        s->next=first->next;
        first->next=s;
    }
}

2）尾插法

使用尾插法的有参构造函数，构造循环链表的主体部分与单链表一致，区别在于建表完毕后要将尾指针指回头结点，即 r->next=first

template <class T>
linkList<T>::circleList(T a[],int n){//尾插法的有参构造函数
    first=new Node<T>;
    Node<T> *r=first;
    for(int i=0;i<n;i++){
        Node<T> *s=new Node<T>;
        s->data=a[i];
        r->next=s;
        r=s;
    }
    r->next=first;//将尾指针指回头结点
}

【经典应用】

循环链表能解决许多问题，其中，最经典的，就是对于约瑟夫环问题的解决

约瑟夫环是一个数学的应用问题：已知 n 个人（以编号1，2，3...n分别表示）围坐在一张圆桌周围，从编号为 k 的人开始报数，数到 m 的那个人出列，他的下一个人又从 1 开始报数，数到 m 的那个人又出列，依此规律重复下去，直到圆桌周围的人全部出列，问最后剩下的那个人的编号

解决：使用不带头指针的循环链表即可解决，将初始编号加入循环链表后，开始寻找报数起点，然后从报数起点开始，报数循环到第 m-1 个点，最后将 m-1 号点之后的 m 号点从循环链表中删除即可，重复寻找 m-1 号点删除 m 号点，直到剩下一个结点。

struct Node{
    int data;
    Node *next;
};
int main(){
    int n,m,k;
    cin>>n>>m>>k;

    Node *first=new Node;//头指针
    first->data=1;

    Node *p=first;//工作指针
    for(int i=2;i<=n;i++){
        Node *s=new Node;//新建节点
        s->data=i;
        p->next=s;
        p=p->next;
    }
    p->next=first;//链表尾端指向链表头，构成循环链表

    p=first;
    for(int i=1;i<=k-1;i++)//寻找报数起点
        p=p->next;

    while(p!=p->next){//只剩下一个结点时
        for(int i=1;i<m-1;i++)//循环报数到m之前的一个结点
            p=p->next;

        Node *q=p->next;//第m个元素即要出环的元素
        p->next=q->next;//摘链
        delete q;//删除出换元素

        p=p->next;//继续指向下一元素
    }
    cout<<(p->data)<<endl;
    return 0;
}