Coloring Dominoes(Atcoder-2697)
Problem Description
We have a board with a 2×N grid. Snuke covered the board with N dominoes without overlaps. Here, a domino can cover a 1×2 or 2×1 square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and green. Two dominoes that are adjacent by side should be painted by different colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S1 and S2 in the following manner:
Each domino is represented by a different English letter (lowercase or uppercase).
The j-th character in Si represents the domino that occupies the square at the i-th row from the top and j-th column from the left.Constraints
- 1≤N≤52
- |S1|=|S2|=N
- S1 and S2 consist of lowercase and uppercase English letters.
- S1 and S2 represent a valid arrangement of dominoes.
Input
Input is given from Standard Input in the following format:
N
S1
S2Output
Print the number of such ways to paint the dominoes, modulo 1000000007.
Example
Sample Input 1
3
aab
ccbSample Output 1
6
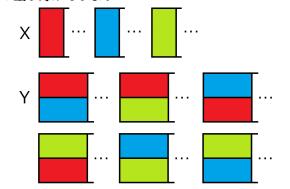
There are six ways as shown below:
Sample Input 2
1
Z
ZSample Output 2
3
Note that it is not always necessary to use all the colors.Sample Input 3
52
RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn
RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzznSample Output 3
95868190
题意:有一个 2*n 大小的区域,上面有 n 个1*2 的牌将所有区域覆盖,现在给出 n 和 n 个牌的排列方式,要在这些牌中涂上三种颜色,要求相邻颜色不同,问有多少中涂色方法
思路:递推
首先考虑最左边的一个或两个矩形,如果最左边是一个竖着的牌,那么涂色情况有三种;如果最左边是两个横着的牌,那么涂色情况有 C(3,1)*C(3,2)=6 种情况
于是,可以根据最左边的情况,向右进行递推:
- 当左边的牌是竖着的牌,右边的牌是竖着的牌,那么在两种颜色中选一个涂,即在原基础上乘以 C(2,1)=2
- 当左边的牌是竖着的牌,右边的牌是两个横着的牌,那么两种颜色都要涂上,即在原基础上乘以 A(2,2)=2
- 当左边的牌是两个横着的牌,右边的牌是竖着的牌,那么右边的牌没有选择,只能涂剩下的那一种颜色,即不做改变
- 当左边的牌是两个横着的牌,右边的牌是两个横着的牌,此时假设左上涂颜色 1,左下涂颜色 2,那么右上只能涂颜色 2 或颜色 3,当右上涂颜色 2 时,右下要么涂颜色 1 要么涂颜色 3;当右上涂颜色 3 时,右下没有选择,只能涂颜色 1,即在原基础上乘以 2+1=3

Source Program
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#include<bitset>
#define EPS 1e-9
#define PI acos(-1.0)
#define INF 0x3f3f3f3f
#define LL long long
const int MOD = 1E9+7;
const int N = 100000+5;
const int dx[] = {-1,1,0,0,-1,-1,1,1};
const int dy[] = {0,0,-1,1,-1,1,-1,1};
using namespace std;
string str1,str2;
int main() {
int n;
scanf("%d",&n);
cin>>str1>>str2;
LL res=1;
int i=0;
int sta;//前一种状态
if(str1[i]==str2[i]){//竖
res*=3;
i++;
sta=1;
}
else{//横
res*=6;
i+=2;
sta=2;
}
while(i<n){
if(str1[i]==str2[i]){//竖
if(sta==1)//前面是竖
res=res*2%MOD;
i++;
sta=1;
}
else{//横
if(sta==1)//前面是竖
res=res*2%MOD;
else//前面是横
res=res*3%MOD;
i+=2;
sta=2;
}
}
printf("%lld\n",res);
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号