pytorch联系及螺旋数据分析

一、pytorch练习

使用torch.Tensor定义数据 ， 可以定义数、向量、二维数组和张量。

import torch
# 可以是一个数
n = torch.tensor(123)
print(n)
# 可以是一维数组（向量）
n = torch.tensor([1,2,3,4,5,6])
print(n)
# 可以是二维数组（矩阵）
n= torch.ones(2,3)
print(n)
# 可以是任意维度的数组（张量）
n = torch.ones(2,3,4)
print(n)

二、螺旋数据分类(sprial classification)

1.下载绘图函数到本地

!wget https://raw.githubusercontent.com/Atcold/pytorch-Deep-Learning/master/res/plot_lib.py

2.产生随机数

import random
import torch
from torch import nn, optim
import math
from IPython import display
from plot_lib import plot_data, plot_model, set_default

# 因为colab是支持GPU的，torch 将在 GPU 上运行
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print('device: ', device)

# 初始化随机数种子。神经网络的参数都是随机初始化的，
# 不同的初始化参数往往会导致不同的结果，当得到比较好的结果时我们通常希望这个结果是可以复现的，
# 因此，在pytorch中，通过设置随机数种子也可以达到这个目的
seed = 12345
random.seed(seed)
torch.manual_seed(seed)

N = 1000  # 每类样本的数量
D = 2  # 每个样本的特征维度
C = 3  # 样本的类别
H = 100  # 神经网络里隐层单元的数量

X = torch.zeros(N * C, D).to(device)
Y = torch.zeros(N * C, dtype=torch.long).to(device)
for c in range(C):
    index = 0
    t = torch.linspace(0, 1, N) # 在[0，1]间均匀的取10000个数，赋给t
    # 下面的代码不用理解太多，总之是根据公式计算出三类样本（可以构成螺旋形）
    # torch.randn(N) 是得到 N 个均值为0，方差为 1 的一组随机数，注意要和 rand 区分开
    inner_var = torch.linspace( (2*math.pi/C)*c, (2*math.pi/C)*(2+c), N) + torch.randn(N) * 0.2
    
    # 每个样本的(x,y)坐标都保存在 X 里
    # Y 里存储的是样本的类别，分别为 [0, 1, 2]
    for ix in range(N * c, N * (c + 1)):
        X[ix] = t[index] * torch.FloatTensor((math.sin(inner_var[index]), math.cos(inner_var[index])))
        Y[ix] = c
        index += 1

print("Shapes:")
print("X:", X.size())
print("Y:", Y.size())

3.使用plot_lib的plot_data函数显示图象。构建线性模型，使用 print(model) 把模型输出，可以看到有两层。

 4.构建双层神经网络模型

learning_rate = 1e-3
lambda_l2 = 1e-5

# 这里可以看到，和上面模型不同的是，在两层之间加入了一个 ReLU 激活函数
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),   #与1代码块的唯一区别，加入了激活函数
    nn.Linear(H, C)
)
model.to(device)

# 下面的代码和之前是完全一样的，这里不过多叙述
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2

# 训练模型，和之前的代码是完全一样的
for t in range(1000):
    y_pred = model(X)
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = ((Y == predicted).sum().float() / len(Y))
    print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
    display.clear_output(wait=True)
    
    # zero the gradients before running the backward pass.
    optimizer.zero_grad()
    # Backward pass to compute the gradient
    loss.backward()
    # Update params
    optimizer.step()

　　

 

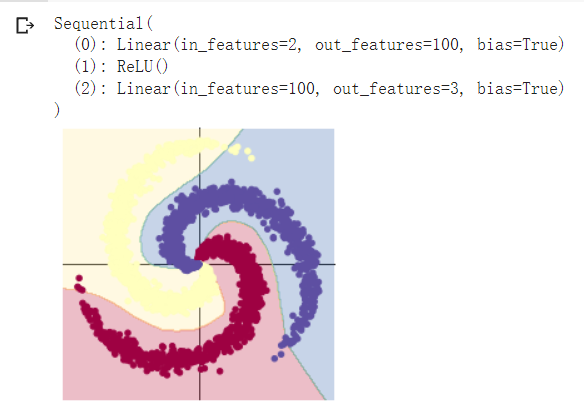
 由于加入了ReLU激活函数取代了Sigmoid函数，ReLU函数速度快，精度高，分类的准确率得到了显著提高。