python习题

简单例题
复杂例题
null

简单例题

1.计算偶数的和

方法一：
sum = 0
for i in range(2, 101, 2):
    sum += i
print(sum)
方法二：
sum = 0
for i in range(1, 101):
    if i % 2 == 0:
        sum += i
    else:
        continue
print(sum)

2.计算1-2+3-4……

n = eval(input("请输入n"))
s = 0;sign = 1
for i in range(1, n + 1):
    s = s + sign * n
    sign = - sign
print(s)

3.判断n是否为素数(升级后，判断300以内的素数）

方法一：
n = eval(input("请输入一个大于二的数"))
i = 0;count = 0;sum = 0
for i in range(2, n):
    if n % i == 0:
        break
if i == n - 1:
    print(n,"是素数")
方法二：
n = eval(input("请输入一个大于二的数"))
i = 0;count = 0;sum = 0
for i in range(2, n):
    if n % i == 0:
        break
else:
    print(n,"是素数")
300以内素数
n = eval(input("请输入一个大于二的数"))
i = 0;count = 0;sum = 0
for n in range(300):
    for i in range(2, n):
        if n % i == 0:
            break
    else:
        print(n,"是素数")

4.计算圆周率pi

import random as r
s = eval(input(""))
n = 0
for i in range(1, s + 1):
    x, y = random.random()
    if x ** 2 +y ** 2 < 1:
        n += 1
pi = 4 * (n / s)

5.斐波那契数列

n = eval(input(""))
a = b = 1
print(a, b)
for i in range(3, n + 1):
    c = a + b
    print(c)
    a = b
    b = c
五个一行怎么写？
n = eval(input(""))
a = b = 1
print("{:<4} {:<4} ".format(a, b),end = " ")
for i in range(3, n + 1):
    c = a + b
    print("{:<4}".format(c),end = " ")
    if i % 5 == 0:
        print()
    a = b
    b = c

6.将十进制转化为八进制

n = int(input())
for i in range(n):
    if n <= 10:
        s = input()
        if len(s) <= 100000:
            res_1 = int(s, 16)
            res_2 = oct(res_1)
            print(res_2[2:])

7.杨辉三角

n = int(input())
nums = [[0] * n for i in range(n)]
for i in range(n):
    for j in range(n):
        if j == 0:
            nums[i][j] = 1
        else:
            nums[i][j] = nums[i - 1][j - 1] + nums[i - 1][j]
        if nums[i][j] != 0:
            print(nums[i][j], end = " ")
    print()

8.查找英文单词中出现最多的字母

word = input()
arr = [0 for i in range(26)]
for alpha in word:
    arr[ord(alpha) - 97] += 1
num = max(arr)
alp = chr(arr.index(num) + 97)
print(alp)
print(num)

9.查找整数

n = int(input())
arr = input().split()
a = input()
i = 0
while i < n:
    if a == arr[i]:
        print(i + 1)
        break
    i += 1
if i == n:
    print(-1)

10.分解质因数

def decPrime(num):
    lt = []
    print(num, "=", end = "", sep = "")
    while num != 1:
        for i in range(2, int(num + 1)):
            if num % i == 0:
                lt.append(i)
                num = num / i
                break
    for i in range(0, len(lt) - 10):
        print(lt[i], "*", end = "", sep = "")
    print(lt[-1])
i, j =map(int, input().split())
for k in range(i ,j + 1):
    decPrime(k)

11.1， 2， 3， 4可以组成多少不同的四位数

s = 0
count = 0
lis = []
for i in range(1, 5):
    for j in range(1, 5):
        for z in range(1, 5):
            if i != j and i != z and j != z:
                s = i * 100 + j * 10 + z
                lis.append(s)
                count += 1
print(lis)
print(count)

12.一个整数它加上一百是完全平方数，再加上168又是一个完全平方数，请问该数是

import math
def judge(n):
    a = str(math.sqrt(n))
    b, c = a.split(".")
    count = 0
    lis = ["1", "2", "3", "4", "5", "6", "7", "8", "9"]
    for i in range(len(c)):
        if c[i] == "0":
            count += 1
    if count == len(c):
        return True
    else:
        return False
c = judge(289)
for i in range(1000):
    a = i + 100
    b = i + 168 + 100
    c = judge(b)
    d = judge(a)
    if c and d:
        print("%d是"%i)

13.输入年月日，判断今天是这一年的第几天

year = int(input("year:\n"))
month = int(input("month:\n"))
day = int(input("day:\n"))
sum = 0
months = [0, 31, 59, 90, 120, 181, 212, 243, 273, 304, 334]
if 0 < month <= 12:
    sum = months[month - 1]
else:
    print("day error")
sum += day
leap = 0
if (year % 400 == 0) or ((year % 4 == 0) and (year % 100 != 0)):
    leap = 1
if (leap == 1) and (month > 2):
    sum += 1
print(sum)

14.判断三个数字的大小

lis = []
for i in range(3):
    a = int(input('请输入一个数字：'))
    lis.append(a)
lis.sort()
print(lis)

15.数组排序并连接

lis1 = []
lis2 = []
for i in range(3):
    a = int(input("请输入一个数字："))
    lis1.append(a)
for i in range(3):
    b = int(input("请输入一个数字:"))
    lis2.append(b)
lis1.sort()
lis2.sort()
print(lis1 + lis2)

16.九九乘法表

左三角
for i in range(1, 10):
    for j in range(1, i + 1):
        print("%d * %d = %d"%(i, j, i * j), end = "\t")
    print()
右三角
for i in range(1, 10):
    print(" " * 12 * (i - 1), end = "")
    for j in range(9, i - 1, -1):
        print("%d * %d = %d" % (i, j, i * j), end="\t")
    print()

17.简单版购物车

#菜鸟整体做到了第八题
product = [["华为", 6680], ["wine", 1488], ["book", 80], ["shoes", 799], ["matebook", 5800]]
for i in product:
    print(i)
carts = []
while True:
    num = input("请输入产品编号")
    if num.isdigit():
        if 1 <= int(num) <= 4:
            if num in carts:
                print("商品已经在购物车中")
            else:
                carts.append(num)
                print("商品%s已经在添加到购物车"%product[int(num) - 1][0])
        else:
            print("你输入的商品序号不在范围内")
    elif num.upper() == "Q":
        break
    else:
        print("请输入数字")
for j in carts:
    print(product[int(j) - 1][0])

18.词频分析

import jieba
with open("唐诗三百首.txt", "r", encoding = "utf-8") as f:
    txt = f.read()
words = jieba.lcut(txt)
stopwords = [line.strip() for line in open("中文停用词".txt, "r", encoding = "utf-8")]
count = {}
for word in words:
    if len(word) > 1 and word not in stopwords:
        count[word] = count.get(word, 0) + 1
items = list(count.items())
items.sort(key = lambda x:x[1], reverse = True)
total = min(30, len(items))
for i in range(total):
    word, count = items[i]
    print("%6s(%2d)"%(word, count), end = " ")
    if (i + 2) % 5 == 0:
        print()
print()

19.生成随机数并排序

方法一：
import random
a = [random.randint(20, 100) for i in range(1000)]
b = set(a)
b = list(b)
b.sort()
print(b)
方法二：
import random
a = [random.randint(20, 100) for i in range(1000)]
b = {}
for i in a:
    b[i] = b.get(i , 0) + 1
c = list(b.items())
c.sort(key = lambda x:x[1])
for i in range(len(c)):
    num, count = c[i]
    print(num, count)

20.字母转化为数字

21.汉诺塔次数

def hanuota(n):
  if n == 1:
    return 1
  else:
    return 2 * hanuota(n - 1) + 1
print(hanuota(64))

22.黄金比率

a1 = 1
a2 = 3
a3 = a1 + a2
while True:
  a1, a2 = a2, a3
  a3 = a1 + a2
  t = a2 / a3
  t = round(t, 6)
  if t == 0.618034:
    break
print("%d/%d"%(a2, a3))

23.斐波那契数列兔子问题

方法一：
f1 = 1
f2 = 1
for i in range(1, 22):
    print("%12ld %12ld"%(f1, f2), end = "")
    if(i % 3 == 0):
        print()
    f1 = f1 + f2
    f2 = f1 + f2 
方法二：
def func(n):
    if n < 3:
        return 1
    else:
        return func(n - 1) + func(n - 2)

24.打印出所有的水仙花

方法一：
for i in range(100, 1000):
    g = i % 10
    s = i % 100 // 10
    b = i // 100
    if i == g ** 3 +s ** 3 + b ** 3:
        print(i)
方法二：
for i in range(100, 1000):
    s = str(i)
    if int(s[0]) ** 3 + int(s[1]) ** 3 + int(s[2]) ** 3 == i:
        print(i)

25.将一个正整数分解质因数

def reduceNum(n):
    print ('{} = '.format(n), end=" ")
    if not isinstance(n, int) or n <= 0 :
        print ('请输入一个正确的数字 !')
        exit(0)
    elif n in [1] :
        print ('{}'.format(n))
    while n not in [1] : # 循环保证递归
        for index in range(2, n + 1) :
            if n % index == 0:
                n //= index # n 等于 n//index
                if n == 1: 
                    print (index )
                else : # index 一定是素数
                    print ('{} *'.format(index), end=" ")
                break
reduceNum(90)
reduceNum(100)
--自己去还没有做出来

26.将分数排序

score = int(input('输入分数:\n'))
if score >= 90:
    grade = 'A'
elif score >= 60:
    grade = 'B'
else:
    grade = 'C'
 
print ('%d 属于 %s' % (score,grade))

27.小明想找到两个正整数 XXX 和 YYY，满足

2019<X<Y2019 < X < Y2019<X<Y;
20192,X2,Y22019^2, X^2, Y^220192,X2,Y2 组成等差数列。

请你求出在所有可能的解中，X+YX + YX+Y 的最小值是多少？

from math import sqrt
t=[]
for x in range(2020,100000):
    y=sqrt(2*x*x-2019*2019)
    if int(y)==y:
        print(int(x+y))
        break

28.看这个算式：

☆☆☆ + ☆☆☆ = ☆☆☆
如果每个五角星代表 111 ~ 999 的不同的数字。
这个算式有多少种可能的正确填写方法？

29.猴子吃桃

x2 = 1
for day in range(9, 0, -1):
      x1 = (x2 + 1) * 2
      x2 = x1
print(x1)

30.统计字符个数

import string
s = raw_input('请输入一个字符串:\n')
letters = 0
space = 0
digit = 0
others = 0
i=0
while i < len(s):
    c = s[i]
    i += 1
    if c.isalpha():
        letters += 1
    elif c.isspace():
        space += 1
    elif c.isdigit():
        digit += 1
    else:
        others += 1
print 'char = %d,space = %d,digit = %d,others = %d' % (letters,space,digit,others)

31.a + aa + aaa

2 + 22 + 222

n = int(input('n = '))
a = int(input('a = '))
sum = 0
total = 0
for i in range(n):
    sum += (10 ** i)
    total += sum * a
print(total)

32.统计完数

for i in range(1, 1001):
    sum = 0
    for j in range(1, i):
        if i % j == 0:
            sum += j
    if sum == i:
        print(i)

33.比赛问题

for a in ['x','y','z']:
    for b in ['x', 'y', 'z']:
        for c in ['x', 'y', 'z']:
            if(a!=b)and(b!=c)and(c!=a) and (a!='x') and (c!='x') and (c!='z'):
                print 'a和%s比赛，b和%s比赛，c和%s比赛' %(a,b,c)

34.计算累乘

def lc(n):
    x = 1
    for i in range(1, n + 1):
        x *= i
    return x
print(lc(3))

35利用递归计算函数的阶乘

def jc(n):
    if n == 1:
        return 1
    else:
        return n * jc(n - 1)
print(jc(3))

36将输入的字符以相反的顺序输出

def xf(argv):
    return argv[::-1]
print(xf("e"))

37.计算年龄

def age(n):
    if n == 1:
        c = 10
    else:
        c = age(n - 1) + 2
    return c
print(age(4))

38.给一个不多于五位的正整数，先求他是几位数，再逆序打印出各位数字

n = int(input("请输入一个整数："))
a = n % 10
b = n // 10 % 10
c = n // 100 % 10
d = n // 1000 % 10
e = n // 10000
if e != 0:
    print("五位数")
elif d != 0:
    print("四位数")
elif c != 0:
    print("三位数")
elif b != 0:
    print("二位数")
else:
    print("一位数")

39.输入一个五位数，判断他是不是回文数

n = input("请输入你要判断的数：")
c = n[::-1]
if n.isdigit():
    if n == c:
        print("%s是回文数"%n)
else:
    print("输入不合法")

40.判断第100002个素数

方法一：
import math
count=0
ss=2
flag=False
while count<100002:
  for i in range(2,int(math.sqrt(ss)+1)):
    if ss%i==0:
      flag=True
      break
  if flag:
    flag=False
  else:
    count+=1
  ss+=1
print(ss-1)
方法二：
import math
def f(num):
  for i in range(2, int(math.sqrt(num))+1):
    if num % i == 0:
      break
  else:
    return 1
num = []
x=2
while True:
  if f(x)==1:
    num.append(x)
  x+=1
  if len(num)==100002:
    print(num[-1])
    break

40.设置文本颜色

class bcolors:
    HEADER = '\033[95m'
    OKBLUE = '\033[94m'
    OKGREEN = '\033[92m'
    WARNING = '\033[93m'
    FAIL = '\033[91m'
    ENDC = '\033[0m'
    BOLD = '\033[1m'
    UNDERLINE = '\033[4m'
print (bcolors.WARNING + "警告的颜色字体?" + bcolors.ENDC)

41.对十个数进行排序，并使用选择排序法

import random
x = []
for i in range(10):
    x.append(random.randint(1, 10))
for i in range(0, 10):
    for j in range(i, 10):
        if x[i] < x[j]:
            x[i], x[j] = x[j], x[i]
print(x)

42.求一个三乘三矩阵对角线元素之和

import random
a = []
sum = 0
for i in range(3):
    b = [random.randint(1, 10) for j in range(3)]
    a.append(b)
for i in range(3):
    sum += a[i][i]
print(sum)

43.有一个已近排好序的数组，现在想按照原来的规则将一个数插入

import random
a = [random.randint(1, 10) for j in range(10)]
a.sort()
print(a)
n = int(input("请输入你要插入的数"))
for i in range(9):
    if a[i] <= n < a[i + 1]:
        a.insert(i + 1, n)
        break
for i in range(9):
    if n < a[i]:
        break
else:
    a.insert(10, n)
for i in range(9):
    if n > a[i]:
        break
else:
    a.insert(0, n)
print(a)

44.将一个数组逆序输出，用第一个和最后一个交换

import random
c = random.randint(1, 20)
a = [random.randint(1, 10) for i in range(c)]
print(a)
for i in range(len(a) // 2):
    a[i], a[len(a) - i - 1] = a[len(a) - i - 1], a[i]
print(a)

45.学习使用auto定义变量的用法

num = 2
def autofunc():
    num = 1
    print ('internal block num = %d' % num)
    num += 1
for i in range(3):
    print ('The num = %d' % num)
    num += 1
    autofunc()

46.学习使用按位与&和或，按位异或^

if __name__ == '__main__':
    a = 0x77
    b = a & 3
    print ('a & b = %d' % b)
    b &= 7
    print ('a & b = %d' % b)
if __name__ == '__main__':
    a = 0o77
    b = a | 3
    print ('a | b is %d' % b)
    b |= 7
    print ('a | b is %d' % b)
if __name__ == '__main__':
    a = 0o77
    b = a ^ 3
    print ('The a ^ 3 = %d' % b)
    b ^= 7
    print ('The a ^ b = %d' % b)

47.输入数组，最大的与第一个元素交换，最小的于最后一个元素交换，输出数组

--方法一：
a = []
for i in range(6):
    n = int(input("请输入一个数："))
    a.append(n)
for i in range(6):
    for j in range(6):
        if a[i] < a[j]:
            break
    else:
        a[0], a[i] = a[i], a[0]
for i in range(6):
    for j in range(6):
        if a[i] > a[j]:
            break
    else:
        a[5], a[i] = a[i], a[5]
print(a)
--方法二：
import numpy as np
a = []
for i in range(5):
    a.append(input("Please input a number: "))
print a
a = np.array(a)
#得到最大值的索引
max_index = np.argmax(a)
#得到最小值的索引
min_index = np.argmin(a)
a[0], a[max_index] = a[max_index], a[0]
a[-1], a[min_index] = a[min_index], a[-1]
print a

48.有n个整数，使其前面各数顺序向后移m个位置，最后m个数变成最前面m个数

方法一：
if __name__ == '__main__':
    n = int(raw_input('整数 n 为:\n'))
    m = int(raw_input('向后移 m 个位置为:\n'))
 
    def move(array,n,m):
        array_end = array[n - 1]
        for i in range(n - 1,-1,- 1):
            array[i] = array[i - 1]
        array[0] = array_end
        m -= 1
        if m > 0:move(array,n,m)
        
    number = []
    for i in range(n):
        number.append(int(raw_input('输入一个数字:\n')))
    print '原始列表:',number
 
    move(number,n,m)
 
    print '移动之后:',number
方法二：
import random
n = int(input("请输入你要的整数个数："))
m = int(input("请输入你要移动的位数："))
lis = [random.randint(0, 9) for i in range(n)]
new_lis = lis[m::] + lis[0:m]
print(lis)
print(new_lis)
方法三：
n=int(input("输入整数1~n:"))
List=[]
for i in range(1,n+1):
    List.append(i)
print("打印1~n:",List)
print()
m=int(input("输入要移动的位数:"))
List2=List[n-m:n+1]+List[0:n-m]
print("打印移动后的结果:",List2)

49.有n个人围成一圈，顺序排号。从第一个人开始报数（从1到3报数），凡报到3的人退出圈子，问最后留下的是原来第几号的那位。

方法一：
#coding=utf-8
from collections import deque
#添加进列表
a=[]
n=input('请输入几个人：')
for i in range(1,n+1):
    a.append(i)
b=deque(a)   # 使用双段队列deque,目的是使用里面的方法回转rotate
#创建删除符合3的数并且回转列表
while True:
    b.remove(b[2])   #删除为3的数也就是索引为2的数
    b.rotate(-2)     #将第三个数后面的数进行回转从头开始
    if len(b)==2:    
        print b[1]   #最后剩两个数，那么最后的人一定是最后一个数
        break
方法二：
# coding:utf-8
n=int(input("输入人数:"))
List=[]
for i in range(1,n+1):
    List.append(i)

sum=0
while 1:
    t=0;
    for i in range(1,len(List)+1):
        sum=sum+1
        if (sum)%3==0:
            List.pop(i-1-t)
            t=t+1

    if len(List)==1:
        print("最后留下的是原来第%d号的那位" % List[0])
        break
方法三：
if __name__ == '__main__':
    nmax = 50
    n = int(raw_input('请输入总人数:'))
    num = []
    for i in range(n):
        num.append(i + 1)
 
    i = 0
    k = 0
    m = 0
 
    while m < n - 1:
        if num[i] != 0 : k += 1
        if k == 3:
            num[i] = 0
            k = 0
            m += 1
        i += 1
        if i == n : i = 0
 
    i = 0
    while num[i] == 0: i += 1
    print num[i]

50.编写一个函数，输入n为偶数时，调用函数求1/2+1/4+...+1/n,当输入n为奇数时，调用函数1/1+1/3+...+1/n

def peven(n):
    i = 0
    s = 0.0
    for i in range(2,n + 1,2):
        s += 1.0 / i   # Python里，整数除整数，只能得出整数，所以需要使用 浮点数 1.0
    return s
 
def podd(n):
    s = 0.0
    for i in range(1, n + 1,2):
        s += 1.0 / i    # Python里，整数除整数，只能得出整数，所以需要使用 浮点数 1.0
    return s
 
def dcall(fp,n):
    s = fp(n)
    return s
 
if __name__ == '__main__':
    n = int(raw_input('input a number:\n'))
    if n % 2 == 0:
        sum = dcall(peven,n)
    else:
        sum = dcall(podd,n)
    print sum
方法四：自己写的错误代码
n = int(input('请输入总人数：'))
lis = []
for i in range(n):
    lis.append(i + 1)
a = 1
b = 2
c = 3
d = len(lis)
ls = lis
while len(lis) > 1:
    d = len(lis)

    for i in range(1, d + 1):
        if i % 3 == 0:
            a = lis[i - 1]
            ls.remove(a)
print(lis)

50.person = {"li":18,"wang":50,"zhang":20,"sun":22}，找出年龄最大的人

person = {"li":18,"wang":50,"zhang":20,"sun":22}
lis = list(person.items())
lis.sort(key = lambda x: x[1], reverse = True)
print(lis)
print(lis[0][0])

51.猴子分桃，不会，而且看不懂

i = 0
j = 1
x = 0
while (i < 5) :
    x = 4 * j
    for i in range(0,5) :
        if(x%4 != 0) :
            break
        else :
            i += 1
        x = (x/4) * 5 +1
    j += 1
print(x)

52.八进制转换为十进制

方法一：
n = int(input("请输入一个八进制数："))
sum = n % 10
a = n // 10
count = 1
while a != 0:
    b = a % 10
    sum += a * 8 ** count
    a = a // 10
    count += 1
print(sum)
方法二：
 n = 0
    p = raw_input('input a octal number:\n')
    for i in range(len(p)):
        n = n * 8 + ord(p[i]) - ord('0')
    print n

53.输入一个奇数，然后判断最少几个 9 除于该数的结果为整数。

n = int(input("请输入一个奇数："))
a = 9
b = a / n
while b != 0:
    a = a * 10 + 9
    b = a % n
print(a)

54.有两个磁盘文件A和B,各存放一行字母,要求把这两个文件中的信息合并(按字母顺序排列), 输出到一个新文件C中

if __name__ == '__main__':
    import string
    fp = open('test1.txt')
    a = fp.read()
    fp.close()
 
    fp = open('test2.txt')
    b = fp.read()
    fp.close()
 
    fp = open('test3.txt','w')
    l = list(a + b)
    l.sort()
    s = ''
    s = s.join(l)
    fp.write(s)
    fp.close()

复杂例题

1.请你找到最小的整数 XXX 同时满足：

XXX 是 201920192019 的整倍数；
XXX 的每一位数字都是奇数。

--超时方法：
lis = []
for i in range(2019, 10000000000, 2019):
  stri = str(i)
  for j in stri:
    if int(j) % 2 == 0:
      break
  else:
    lis.append(i)
print(lis[0])
--速度更快，但是不知道方法是不是最好
lis = []
for i in range(2019, 10000000000, 2019):
  if len(lis) > 0:
    break
  stri = str(i)
  for j in stri:
    if int(j) % 2 == 0:
      break
  else:
    lis.append(i)
print(lis[0])
--别人的方法，挺好的
def main():
  flag = False
  for x in range(100):
    # 2019
    data = str(x*2019)
    for y in data:
      if int(y)%2==0:
        break
    else:
      print(data)
main()
--别人的方法，这个也还可以
def check(n):
    n = str(n)
    for i in n:
        if int(i) % 2 == 0:
            return False
    return True

n = 2019
while True:
    if check(n):
        break
    n += 2019
print(n)

2.你一定听说过这个故事。国王对发明国际象棋的大臣很佩服，问他要什么报酬，大臣说：请在第 111 个棋盘格放 111 粒麦子，在第 222 个棋盘格放 222 粒麦子，在第 333 个棋盘格放 444 粒麦子，在第 444 个棋盘格放 888 粒麦子，......后一格的数字是前一格的两倍，直到放完所有棋盘格（国际象棋共有 646464 格）。

国王以为他只是想要一袋麦子而已，哈哈大笑。
当时的条件下无法准确计算，但估算结果令人吃惊：即使全世界都铺满麦子也不够用！
请你借助计算机准确地计算，到底需要多少粒麦子。

很简单，就不写代码了

3.古埃及曾经创造出灿烂的人类文明，他们的分数表示却很令人不解。古埃及喜欢把一个分数分解为类似： 1/a+1/b1/a + 1/b1/a+1/b 的格式。

这里，aaa 和 bbb 必须是不同的两个整数，分子必须为 111。
比如，2/152/152/15 一共有 444 种不同的分解法（姑且称为埃及分解法）：

--自己做的时候没有想到通分，有点蠢
for x in range(1,1500):
  for y in range(1,1500):
    if 45*(x+y)==2*x*y:
      num+=1
      if x==y:num-=1
print(num//2)

4.小明看到一本书上写着：任何数字的立方都可以表示为连续奇数的和。

比如：
2^3 = 8 = 3 + 5
3^3 = 27 = 7 + 9 + 11
4^3 = 64 = 1 + 3 + ... + 15
[copy]
虽然他没有想出怎么证明，但他想通过计算机进行验证。
请你帮助小明写出 111111111 的立方之连续奇数和表示法的起始数字。如果有多个表示方案，选择起始数字小的方案。

--自己的方法超时
sum = 0
for i in range(1, 8000, 2):
  sum = 0
  for j in range(i, 8000, 2):
    sum += j
    if sum == 111 ** 3:
      print(i)
      break
--别人的方法
a=111**3
b=True
i=1
while(b):
    k=i
    j=i
    while(j<=a):
        k+=2
        j+=k
        if(j==a):
            print(i)
            b=False
            break
    i+=2

3. 小明参加了学校的趣味运动会，其中的一个项目是：跳格子。

地上画着一些格子，每个格子里写一个字，如下所示：（也可参见p1.jpg）
从我做起振
我做起振兴
做起振兴中
起振兴中华

比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。
要求跳过的路线刚好构成“从我做起振兴中华”这句话。
请你帮助小明算一算他一共有多少种可能的跳跃路线呢？

import numpy as np
data = np.zeros((4, 5))
data[0][0] = 1

for i in range(0, 4):
    for j in range(0, 5):
        data[i][j] += data[i - 1][j] + data[i][j - 1]

print(data[3][4])
方法二：
def ans(a, b):
    if a == 0 or b == 0:
        return 1
    else:
        return ans(a - 1, b) + ans(a, b - 1)


res = ans(3, 4)
print(res)

4.小明正看着 203879203879203879 这个数字发呆。

原来，203879∗203879=41566646641203879 * 203879 = 41566646641203879∗203879=41566646641。
这有什么神奇呢？仔细观察，203879203879203879 是个 666 位数，并且它的每个数位上的数字都是不同的，并且它平方后的所有数位上都不出现组成它自身的数字。
具有这样特点的 666 位数还有一个，请你找出它！
再归纳一下筛选要求：
666 位正整数；
每个数位上的数字不同；
其平方数的每个数位不含原数字的任何组成数位。

for i in range(123456, 987654):
  a = str(i)
  lis1 = []
  lis2 = []
  for j in a:
    lis1.append(j)
    b = i * i
    b = str(b)
    for k in b:
      lis2.append(k)
  if not (set(lis1) & set(lis2)) and (len(lis1) == len(set(lis1))):
    print(i)

5.把 abcd...sabcd...sabcd...s 共19个字母组成的序列重复拼接 106106106 次，得到长度为 201420142014 的串。

接下来删除第 111 个字母（即开头的字母 aaa），以及第 333 个，第 555 个等所有奇数位置的字母。
得到的新串再进行删除奇数位置字母的动作。如此下去，最后只剩下一个字母，请输出该字母。

方法一：
import os
import sys

str= "abcdefghijklmnopqrs"*106
while len(str)!= 1:
    str = str[1::2]
print(str)
方法二：
import os
import sys

# 请在此输入您的代码

s = list("abcdefghijklmnopqrs"*106)

ans = 0
while len(s) != 1:
    for i in range(len(s)):
        if i % 2 == 0:
            s[i] = 0
    while 0 in s:
        s.remove(0)

print(s[0])

6.话说大诗人李白，一生好饮。幸好他从不开车。

一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：
无事街上走，提壶去打酒。逢店加一倍，遇花喝一斗。
这一路上，他一共遇到店5次，遇到花 101010 次，已知最后一次遇到的是花，他正好把酒喝光了。
请你计算李白遇到店和花的次序，可以把遇店记为 aaa，遇花记为 bbb 。则：babaabbabbabbbbbabaabbabbabbbbbabaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。

import os
import sys
# 请在此输入您的代码
def libai(dian,hua,jiu):
    global sum
    if dian>0:
        libai(dian-1,hua,jiu*2)
    if hua>0:
        libai(dian,hua-1,jiu-1)
    if dian==0 and hua==1 and jiu==1:
        sum+=1
    return sum
sum = 0
print(libai(5,10,2))
递归，下次遇到这种情况，记得用递归

7.有一个 666 位的正整数，它有个很神奇的性质：

分别用 2,3,4,5,62, 3, 4, 5, 62,3,4,5,6 去乘它，得到的仍然是 666 位数，并且乘积中所包含的数字与这个 666 位数完全一样！只不过是它们的顺序重新排列了而已。
请计算出这个 666 位数。

import os
import sys
for i  in range(100000,166667):
  goal = sorted(str(i))
  x2 = sorted(str(i*2))
  x3 = sorted(str(i*3))
  x4 = sorted(str(i*4))
  x5 = sorted(str(i*5))
  x6 = sorted(str(i*6))
  if x2 == goal and x3 == goal and x4 == goal and x5 == goal and x6 == goal:
    print(i)

8.小明的作业本上有道思考题：

看下面的算式：
(□□□□-□□□□)□□=900
其中的小方块代表 000 ~ 999 的数字，这 101010 个方块刚好包含了 000 ~ 999 中的所有数字。注意：000 不能作为某个数字的首位。
小明经过几天的努力，终于做出了答案！如下：
(5012-4987)36=900
用计算机搜索后，发现还有另外一个解，本题的任务就是：请你算出这另外的一个解

import os
import sys
import itertools

count = 0
li = []
for num in itertools.permutations(range(10)):
    a = num[0]*1000+num[1]*100+num[2]*10+num[3]
    b = num[4]*1000+num[5]*100+num[6]*10+num[7]
    c = num[8]*10+num[9]
    if (a-b)*c == 900:
        li.append((a,b,c))

print("(%d-%d)*%d=900"%(li[1][0],li[1][1],li[1][2]))

9.小明发现了一个奇妙的数字。它的平方和立方正好把 000 ~ 999 的 101010 个数字每个用且只用了一次

for i in range(10,100):
    a=str(i**2)+str(i**3)
    b=set(a)
    if len(a)==len(b)==10:
        print(i)
我没有想到，很棒的方法

10.如果把一个正整数的每一位都平方后再求和，得到一个新的正整数。对新产生的正整数再做同样的处理。

如此一来，你会发现，不管开始取的是什么数字，最终如果不是落入 111，就是落入同一个循环圈。
请输出这个循环圈中最大的那个数字。

num = 2
lst=list(map(int,str(num)))
tmp=[]
for _ in range(100):
    num=0
    for i in lst:
        num += i**2
    tmp.append(num)
    lst=list(map(int,str(num)))
print(max(tmp))
不懂，没有看懂什么意思

11.2,3,5,7,11,13,.... 是素数序列。类似：7,37,67,97,127,1577,37,67,97,127,1577,37,67,97,127,157 这样完全由素数组成的等差数列，叫等差素数数列。

上边的数列公差为 303030，长度为 666。
200420042004 年，格林与华人陶哲轩合作证明了：存在任意长度的素数等差数列。这是数论领域一项惊人的成果！
有这一理论为基础，请你借助手中的计算机，满怀信心地搜索：
长度为 101010 的等差素数列，其公差最小值是多少？

import os
import sys
import math
def isPrime(n):
  if n <= 1:
    return False
  for i in range(2,int(math.sqrt(n))+1):
    if n % i == 0:
      return False
  return True

for i in range(1,10000):
  if isPrime(i):
    for j in range(200,300):
      for z in range(1,10):
        if not isPrime(i+z*j):
          break
        if z == 9:
          print(j)

12.观察如下的算式：

9213×85674=7893145629213 \times 85674 = 7893145629213×85674=789314562
左边的乘数和被乘数正好用到了 111 ~ 999 的所有数字，每个 111 次。而乘积恰好也是用到了 111 ~ 999 的所有数字，并且每个 111 次。
请你借助计算机的强大计算能力，找出满足如上要求的 999 数算式一共有多少个？

答案
import os
import sys
from itertools import *
cnt = 0
for i in permutations(['1','2','3','4','5','6','7','8','9'] ):
    for j in range(1, 9):
        a, b = int(''.join(i[:j])), int(''.join(i[j:]))
        if a>=b:
            c = str(a*b)
            if len(set(c)) == 9 and len(c) == 9 and '0' not in c:
                cnt += 1
print(cnt)
print(1625) #11秒左右
自己的错误代码
lis1 = []
lis2 = []
for i in range(1, 10):
  for j in range(1, 10):
    if i == j:
      continue
    for z in range(1, 10):
      if z == i or z == j:
        continue
      for k in range(1, 10):
        if k == i or k == j or k == z:
          continue
        x = i * 1000 + j * 100 + z * 10 + k
        lis1.append(x)
for i in range(1, 10):
  for j in range(1, 10):
    if i == j:
      continue
    for z in range(1, 10):
      if z == i or z == j:
        continue
      for k in range(1, 10):
        if k == i or k == j or k == z:
          continue
          for l in range(1, 10):
            if i == l or j == l or z == l or k == l:
              continue
            y = i * 10000 + j * 1000 + z * 100 + k * 10 + l
            lis2.append(y)
count = 0
for m in lis1:
  for n in lis2:
    a = str(m) + str(n)
    a = set(list(a))
    if len(a) == 9:
      c = m * n
      c = set(list(str(c)))
      if len(c) == 9:
        count += 1

13.W星球的长老交给小明一个任务： 1,2,3⋯161,2,3 \cdots 161,2,3⋯16 这 161616 个数字分为两组。

要求：这两组数字的和相同，并且，两组数字的平方和也相同，并且，两组数字的立方和也相同。
请你利用计算机的强大搜索能力解决这个问题。并输出 111 所在的那个分组的所有数字。
这些数字要从小到大排列，两个数字间用一个空格分开。即类似：1 4 5 8...1\ 4\ 5\ 8 ...1 4 5 8... 这样的答案。

数字划分
import itertools
ls = [i for i in range(1, 17)]
sum1 = sum(ls)
sum2 = 0
sum3 = 0
for j in ls:
    sum2 += j*j
for h in ls:
    sum3 += h*h*h
for n in itertools.combinations(ls,8):
    i = list(n)
    _sum2 = 0
    _sum3 = 0
    if sum(i) == (sum1//2):
        for a in i:
            _sum2 += a*a
        for b in i:
            _sum3 += b*b*b
        if _sum2==(sum2//2) and _sum3==(sum3//2):
            if 1 in i:
                for m in i:
                    print(m,end=' ')
我的错误代码
import os
import sys
import random
a = True
lis = [i for i in range(1, 17)]
while a:
  lis2 = random.sample(lis, 8)
  lis1 = [i for i in lis if i not in lis2]
  q1 = 0
  q2 = 0
  w1 = 0
  w2 = 0
  e1 = 0
  e2 = 0
  q1 = sum(lis2)
  q2 = sum(lis1)
  if q1 = q2:
    w1 = sum(map(lambda x: x ** 2), lis1)
    w2 = sum(map(lambda x: x ** 2), lis2)
    if w1 == w2:
      e1 = sum(map(lambda x: x ** 2), lis1)
      e2 = sum(map(lambda x: x ** 2), lis2)
      if e1 == e2:
        if 1 in lis1:
          print(' '.join(sort(lis1)))
        else:
          print(' '.join(sort(lis2)))

14.由 000 ~ 999 这 101010 个数字不重复、不遗漏，可以组成很多 101010 位数字。这其中也有很多恰好是平方数（是某个数的平方）。

比如：102675384910267538491026753849，就是其中最小的一个平方数。
请你找出其中最大的一个平方数是多少？

for i in range(100000, 90000, -1):
  a = i ** 2
  b = set(list(str(a)))
  if len(b) == 10:
    print(a)
    break
别人的方法：
import os
import sys
import math
L = [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
V = []
flag = True
def DFS(v):
    global flag
    if flag:
        if len(v) == 10:
            temp = 0
            for i in range(10):
                temp = temp * 10 + v[i]
            if math.sqrt(temp) == int(math.sqrt(temp)):
                print(temp)
                flag = False
                return 1
        for i in L:
            if i not in v:
                v.append(i)
                DFS(v)
                del v[-1]
DFS([])

15.把 111 ~ 999 这 999 个数字分成两组，中间插入乘号，有的时候，它们的乘积也只包含 111 ~ 999 这 999 个数字，而且每个数字只出现 111 次。

比如：
984672 * 351 = 345619872
98751 * 3462 = 341875962
9 * 87146325 = 784316925
...
符合这种规律的算式还有很多，请你计算在所有这些算式中，乘积最大是多少？
注意，需要输出的是一个整数，表示那个最大的积，只输出乘积，不要输出整个算式。

import os
import sys
from itertools import *
lst=[]
for i in permutations([str(x) for x in range(1,10)]):
  i = "".join(i)
  for j in range(1,9):
    tmp = str(int(i[:j])*int(i[j:]))
    if len(set(tmp))==9 and '0' not in tmp:
      lst.append(int(tmp))
print(max(lst))
print("839542176")
不会

16.如下的 101010 行数据，每行有 101010 个整数，请你求出它们的乘积的末尾有多少个零？
5650 4542 3554 473 946 4114 3871 9073 90 4329
2758 7949 6113 5659 5245 7432 3051 4434 6704 3594
9937 1173 6866 3397 4759 7557 3070 2287 1453 9899
1486 5722 3135 1170 4014 5510 5120 729 2880 9019
2049 698 4582 4346 4427 646 9742 7340 1230 7683
5693 7015 6887 7381 4172 4341 2909 2027 7355 5649
6701 6645 1671 5978 2704 9926 295 3125 3878 6785
2066 4247 4800 1578 6652 4616 1113 6205 3264 2915
3966 5291 2904 1285 2193 1428 2265 8730 9436 7074
689 5510 8243 6114 337 4096 8199 7313 3685 211

方法一：
import os
import sys
data="""5650 4542 3554 473 946 4114 3871 9073 90 4329 
2758 7949 6113 5659 5245 7432 3051 4434 6704 3594 
9937 1173 6866 3397 4759 7557 3070 2287 1453 9899 
1486 5722 3135 1170 4014 5510 5120 729 2880 9019 
2049 698 4582 4346 4427 646 9742 7340 1230 7683 
5693 7015 6887 7381 4172 4341 2909 2027 7355 5649 
6701 6645 1671 5978 2704 9926 295 3125 3878 6785 
2066 4247 4800 1578 6652 4616 1113 6205 3264 2915 
3966 5291 2904 1285 2193 1428 2265 8730 9436 7074 
689 5510 8243 6114 337 4096 8199 7313 3685 211"""
data_array=[]
for i in data.split():
   data_array.append(i)
num=1
for i in data_array:
   num*=int(i)
nums=list(str(num))
ans=0
for i in range(len(nums)-1,0,-1):
   if nums[i]=='0':
      ans+=1
   else:
      break
print(ans)
方法二：
import os
import sys
nums = []
for i in range(10):
    nums.append(list(map(int,input().split())))
res = 1
for i in range(10):
    for j in range(10):
        res *= nums[i][j]
count = 0
for i in str(res)[::-1]:
    if i == '0':
        count += 1
    else:
        break
print(count)
print(31)

C语言做法不是很懂

16.今有 100100100 根绳子，当然会有 200200200 个绳头。

如果任意取绳头两两配对，把所有绳头都打结连接起来。最后会形成若干个绳圈（不考虑是否套在一起）。
我们的问题是：请计算最后将形成多少个绳圈的概率最大？(不会）

import os
import sys
a=[[0 for i in range(101)] for i in range(101)]
a[1][1]=1
for i in range(2,len(a)):
    for j in range(1,len(a[i])):
        if i<j:
            break
        else:
            a[i][j]=a[i-1][j]*(2*i-2)/(2*i-1)+a[i-1][j-1]/(2*i-1)
Max=0
Max_num=1
for i in range(1,101):
    if Max<a[100][i]:
      Max_num=i
      Max=a[100][i]
print(Max_num)

17.由 444 个不同的数字，组成的一个乘法算式，它们的乘积仍然由这 444 个数字组成。
比如：
210 x 6 = 1260
8 x 473 = 3784
27 x 81 = 2187
都符合要求。
如果满足乘法交换律的算式算作同一种情况，那么，包含上边已列出的 333 种情况，一共有多少种满足要求的算式。

方法一：
import os
import sys
count1=0
count2=0
m=0
for i in range(1,10):
    for j in range(100,999):
        m=i*j
        if 1000<=m<=9999:
            a=str(i)+str(j)
            b=str(m)
            if len(list(set(a)))==len(list(set(b)))==4 and sorted(a)==sorted(b):
                count1 += 1
n=0
for i in range(10,99):
    for j in range(10,99):
        n=i*j
        if 1000<=n<=9999:
            a=str(i)+str(j)
            b=str(n)
            if len(list(set(a)))==len(list(set(b)))==4 and sorted(a)==sorted(b) :
                count2 += 1
print(int(count1 + count2/2))
方法二：
import os
import sys
sum=0
for i in range(999):
  for j in range(i+1,999):
    s=list(str(i)+str(j))
    s.sort()
    t=list(str(i*j))
    t.sort()
    if s==t and 1000<i*j<9999 and len(set(s))==len(set(t))==4 :
        #print(i,'*',j)
      sum+=1
print(sum)

18.扑克序列

A A 2 2 3 3 4 4A\ A\ 2\ 2\ 3\ 3\ 4\ 4A A 2 2 3 3 4 4，一共4对扑克牌。请你把它们排成一行。
要求：两个 AAA 中间有 111 张牌，两个 222 之间有 222 张牌，两个 333 之间有 333 张牌，两个 444 之间有 444 张牌。
请填写出所有符合要求的排列中，字典序最小的那个。
例如：22AA334422AA334422AA3344 比 A2A23344A2A23344A2A23344 字典序小。当然，它们都不是满足要求的答案。

19.小李的店里专卖其它店中下架的样品电视机，可称为：样品电视专卖店。

其标价都是 444 位数字（即千元不等）。

小李为了标价清晰、方便，使用了预制的类似数码管的标价签，只要用颜色笔涂数字就可以了,如下图。

图片描述
这种价牌有个特点，对一些数字，倒过来看也是合理的数字。如：1 2 5 6 8 9 01\ 2\ 5\ 6\ 8\ 9\ 01 2 5 6 8 9 0 都可以。这样一来，如果牌子挂倒了，有可能完全变成了另一个价格，比如：195819581958 倒着挂就是：856185618561，差了几千元啊!!

当然，多数情况不能倒读，比如，111011101110 就不能倒过来，因为 000 不能作为开始数字。

有一天，悲剧终于发生了。某个店员不小心把店里的某两个价格牌给挂倒了。并且这两个价格牌的电视机都卖出去了!

庆幸的是价格出入不大，其中一个价牌赔了 200200200 多，另一个价牌却赚了 800800800 多，综合起来，反而多赚了 558558558 元。

请根据这些信息计算：赔钱的那个价牌正确的价格应该是多少？

方法一：
import os
import sys
lis = []
for i in range(1000,10000):
    count = ''
    k = i
    if i % 10 == 0:
        continue
    for j in range(4):
         t = k % 10
         if t == 6:
             count += '9'
         elif t == 9:
             count += '6'
         elif t in [1,2,5,8,0]:
             count += str(t)
         k = k // 10
    if len(count) == 4:
        le = [i,int(count),int(count) - i]
        lis.append(le)
for i in range(len(lis)):
    for j in range(len(lis)):
        if lis[i][2] + lis[j][2] == 558:
            if -300 < lis[i][2] < -200  and 800 < lis[j][2] < 900:
                sum = lis[i][0]
            if -300 < lis[j][2] < -200  and 800 < lis[i][2] < 900:
                sum  = lis[j][0]
print(sum)
方法二：
import os
import sys
def reverse(n):
    table = {0:0, 1: 1, 2: 2, 3: None, 4: None, 5: 5, 6: 9, 7: None, 8: 8, 9: 6}
    t = list(map(int, str(n)))[::-1]
    t = list(map(table.get, t))
    for i in t:
        if i == None:
            return False
    t = ''.join(map(str, t))
    if t[0] == '0':
        return False
    return int(t)


for i in range(1000, 10000):
    r1 = reverse(i)
    if not r1:
        continue
    if 200 < i - r1 < 300:
        for j in range(1000, 10000):
            r2 = reverse(j)
            if not r2:
                continue

            if r2 - j + r1 - i == 558:
                print(i)
                sys.exit()
方法三：
import os
import sys
"""
1 2 5 8 0倒过来是本身
6 9 倒过来是对方
3 4 7 不能倒过来
"""
def rever(num):
    if num == 6:
        return "9"
    if num == 9:
        return "6"
    if num == 1 or num == 2 or num == 5 or num == 8 or num == 0:
        return str(num)

shao200 = []
duo800 = []

for i in range(1000, 10000):
    if str(i).count("3") > 0 or str(i).count("4") > 0 or str(i).count("7") > 0:       # 如果价钱中有3 4 7三个数的话倒不了，价钱不可能出错
        continue
    elif int(str(i)[3]) == 0:continue   # 排除末尾是0的情况
    else:
        re = int(rever(int(str(i)[3])) + rever(int(str(i)[2])) + rever(int(str(i)[1])) + rever(int(str(i)[0])))
        if 300 > i - re > 200:
            shao200.append([i,re,i-re])
        if 800 < re - i < 900:
            duo800.append([i, re, re-i])

for i in range(len(duo800)):
    for j in range(len(shao200)):
        if duo800[i][2] - shao200[j][2] == 558:
            print(shao200[j][0])
            break
    break

20.小明家住在一条胡同里。胡同里的门牌号都是连续的正整数，由于历史原因，最小的号码并不是从 111 开始排的。

有一天小明突然发现了有趣的事情：如果除去小明家不算，胡同里的其它门牌号加起来，刚好是 100100100！并且，小明家的门牌号刚好等于胡同里其它住户的个数！ ....还有,小明家并不靠边，左右都有邻居。

请你根据这些信息，推算小明家的门牌号是多少？
运行限制

不会
方法一：
import os
import sys
for i in range(1,100):
  num=0
  for j in range(0,100):
    num+=i+j
    if num > 100 and i+j>num-100>i and num-100==j:
        print(num-100)
方法二：
import os
import sys
for i in range(3,19):
    sum=0
    for j in range(2,100):
        for k in range(j,j+i+1):
            sum+=k
            if sum-100==i and i>j:
                print(i)
自己的错误代码
def sm(n):
  lis = []
  sum = 0
  for i in range(n, 100):
    sum += i
    lis.append(i)
    if sum == 100:
      return lis
  
for i in range(2, 100):
  a = sm(i)
  x = len(a)
  if x in a:
    print(x)

21.生成回文数

所谓回文数就是左右对称的数字，比如：

585,5885,123321...585,5885,123321...585,5885,123321...

当然，单个的数字也可以算作是对称的。

小明发现了一种生成回文数的方法：比如，取数字 191919，把它与自己的翻转数相加： 19+91=11019 + 91 = 11019+91=110，如果不是回文数，就再进行这个过程： 110+011=121110 + 011 = 121110+011=121 这次是回文数了。

200200200 以内的数字中，绝大多数都可以在 303030 步以内变成回文数，只有一个数字很特殊，就算迭代了 100010001000 次，它还是顽固地拒绝回文！

请你输出该顽固数字。

别人的代码
import os
import sys
for i in range(1,201):
    count=0
    hui=i
    while str(hui)!=str(hui)[::-1]:
        hui=hui+int(str(hui)[::-1])
        if count>30:
            print(i)
            break
        else:
            count+=1
自己的错误代码
def huiwen(n):
  if str(n) == (str(n))[::-1]:
    return True
  else:
    return False
def diedai(n):
  count = 1
  c = int(str(n) + (str(n))[::-1])
  if huiwen(c):
    diedai(c)
    count += 1
  else:
    return n
  if count > 1000:
    print(n)

  for i in range(1, 200):
    diedai(i)

22.1 ~ 999的数字可以组成 333 个 333 位数，设为：A,B,CA,B,CA,B,C, 现在要求满足如下关系：

B=2∗AB = 2 * AB=2∗A

C=3∗AC = 3 * AC=3∗A

请你输出 AAA 的所有可能答案，数字间用空格分开，数字按升序排列。

方法一：
a=[]
for i in range(100,350):
    j=2*i
    k=3*i
    if 100<j<1000 and 100<k<1000:
        b=str(i)+str(j)+str(k)
        if len(list(set(b)))==9 and ('0' not in b):
            a.append(i)
a.sort()
for m in range(len(a)):
    print(a[m],end=" ")
方法二：
from itertools import permutations
nums = []
for num in permutations(range(1,10)):
    a = num[0]*100+num[1]*10+num[2]
    b = num[3]*100+num[4]*10+num[5]
    c = num[6]*100+num[7]*10+num[8]
    if b == 2*a and c == 3*a:
        nums.append(a)
 
for i in sorted(nums):
    print(i,end=' ')
自己的超时代码
lis = []
for i in range(123, 987):

  for j in range(123, 987):
    if i == j:
      continue
    for z in range(123, 987):
      if i == z or j == z:
        continue
      if j == 2 * i and z == 3 * i:
        m = set(list(str(i) + str(j) + str(z)))
        if len(m) == 9:
          lis.append(i)
lis.sort()
print(" ".join(lis))

23.小明发现了一个奇妙的数字。它的平方和立方正好把 000 ~ 999 的 101010 个数字每个用且只用了一次。

你能猜出这个数字是多少吗？

for i in range(10,100):
    a=str(i**2)+str(i**3)
    b=set(a)
    if len(a)==len(b)==10:
        print(i)

24.X 星球愤怒的小鸟喜欢撞火车！

一根平直的铁轨上两火车间相距 1000 米两火车（不妨称 A 和 B）以时速 10米/秒相对行驶。

愤怒的小鸟从 A 车出发，时速 50米/秒，撞向 B 车，然后返回去撞 A 车，再返回去撞 B 车，如此往复.... 两火车在相距 111 米处停车。

问：这期间愤怒的小鸟撞 B 车多少次？

方法一：
distance = 1000
count = 0
while distance > 1:
    time = distance / 60
    distance -= time * 20
    count += 1
print(int((count + 1) / 2))
方法二：
s=[0]*24
sum1=0
for i in range(1,20):    
    s[i]=(1000-20*sum1)/60  #算的是每次撞击需要的时间，例如t3=(1000-20*(t1+t2))/60
    sum1+=s[i]       

num=0
for i in range(len(s)):
    if s[i]>=1/60: #最后限制1米内，时间就是1/60
        num +=1

if num%2==0:
    print(num//2)
else:
    print((num-1)//2)

25.9 的阶乘等于：362880, 它的二进制表示为：1011000100110000000, 这个数字共有 191919 位。

请你计算，9999 的阶乘的二进制表示一共有多少位？

sum = 1
for i in range(1, 10000):
  sum *= i

a = bin(sum)
print(len(a) - 2)

26.能够表示为某个整数的平方的数字称为“平方数”

虽然无法立即说出某个数是平方数，但经常可以断定某个数不是平方数。因为平方数的末位只可能是：[0,1,4,5,6,9]这 6个数字中的某个。所以，4325435332必然不是平方数。

如果给你一个 2 位或 2位以上的数字，你能根据末位的两位来断定它不是平方数吗？

请计算一下，一个 2位以上的平方数的最后两位有多少种可能性？

count=0
a=[]
for i in range(10,100):
    a.append(str(i**2)[-2::])
print(len(set(a)))

27.看下面的算式：

(□□□□-□□□□)□□=900
其中的小方块代表 0 ~ 9的数字，这 10个方块刚好包含了 0 ~ 9中的所有数字。注意：0不能作为某个数字的首位。
小明经过几天的努力，终于做出了答案！如下
(5012-4987)36=900
用计算机搜索后，发现还有另外一个解，本题的任务就是：请你算出这另外的一个解。
注意：输出格式需要与示例严格一致；括号及运算符号不要用中文输入法；整个算式中不能包含空格。

from itertools import *
for i in permutations([x for x in range(10)]):
  if i[0]!=5 and i[0]!=0 and i[4]!=4 and i[4]!=0 and i[8]!=3 and i[8]!=0 :
    if ((1000*i[0]+100*i[1]+10*i[2]+i[3])-(1000*i[4]+100*i[5]+10*i[6]+i[7]))*(10*i[8]+i[9])==900:
      print("(%d%d%d%d-%d%d%d%d)*%d%d=900"%(i[0],i[1],i[2],i[3],i[4],i[5],i[6],i[7],i[8],i[9]))
'''
print("(6048-5973)*12=900")

28.2,3,5,7,11,13,.... 是素数序列。类似：7,37,67,97,127,157 这样完全由素数组成的等差数列，叫等差素数数列。

上边的数列公差为 30，长度为 6。
2004年，格林与华人陶哲轩合作证明了：存在任意长度的素数等差数列。这是数论领域一项惊人的成果！

有这一理论为基础，请你借助手中的计算机，满怀信心地搜索：

长度为 10 的等差素数列，其公差最小值是多少？

方法一：
def isPrime(n):
  if n <= 1:
    return False
  for i in range(2,int(math.sqrt(n))+1):
    if n % i == 0:
      return False
  return True

for i in range(1,10000):
  if isPrime(i):
    for j in range(200,300):
      for z in range(1,10):
        if not isPrime(i+z*j):
          break
        if z == 9:
          print(j)
方法二：我的超时代码
def sushu(n):
  for i in range(2, n):
    if n % i == 0:
      return False
    return True
lis = []
for i in range(200, 300):
  for j in range(2, 10000):
    for k in range(10):
      a = j + i * k
      lis.append(a)
    for m in lis:
      if not sushu(m):
        break
    else:
      print(i)

29.对于 16进制，我们使用字母 A−F 来表示 10及以上的数字。

如法炮制，一直用到字母 Z，就可以表示 36进制。

小明对数位中含有 2、0、1、9的数字很感兴趣，在 1到 40 中这样的数包括 1、2、9、10至 32、39 和 40，共 28 个，他们的和是 574，平方和是 14362。

注意，平方和是指将每个数分别平方后求和。

请问，在 1 到 2019中，所有这样的数的平方和是多少？

方法一：
lis = ["2", "0", "1", "9"]
sum = 0
for i in range(1, 2020):
  a = str(i)
  for j in a:
    if j in lis:
      sum += i * i
      break
print(sum)
方法二：
sum=0
for i in range(41,2020):
    if('2'in str(i) or'1' in str(i) or '0' in str(i) or '9' in str(i)):
        sum += i**2
print(sum+14362)

30.一个 IPv4 的地址是由点分十进制数表示的，例如 192.168.20.20。

在网络传输时，一般直接把 IPv4 地址的数值部分表示成二进制数在网络中传输。请问，在网络中传输一个 IPv4 地址需要多少个二进制位

print(32)
傻了

31.由于沙之国长年干旱，法师小明准备施展自己的一个神秘法术来求雨。

这个法术需要用到他手中的 494949 张法术符，上面分别写着 111 至 494949 这 494949 个数字。法术一共持续 777 周，每天小明都要使用一张法术符，法术符不能重复使用。
每周，小明施展法术产生的能量为这周 777 张法术符上数字的中位数。法术施展完 777 周后，求雨将获得成功，降雨量为 777 周能量的中位数。
由于干旱太久，小明希望这次求雨的降雨量尽可能大，请大最大值是多少？

print(34)没有懂

32.小蓝正在学习一门神奇的语言，这门语言中的单词都是由小写英文字母组成，有些单词很长，远远超过正常英文单词的长度。小蓝学了很长时间也记不住一些单词，他准备不再完全记忆这些单词，而是根据单词中哪个字母出现得最多来分辨单词。

现在，请你帮助小蓝，给了一个单词后，帮助他找到出现最多的字母和这个字母出现的次数。
输入描述

输入一行包含一个单词，单词只由小写英文字母组成。

对于所有的评测用例，输入的单词长度不超过 1000。
输出描述

输出两行，第一行包含一个英文字母，表示单词中出现得最多的字母是哪个。如果有多个字母出现的次数相等，输出字典序最小的那个。

第二行包含一个整数，表示出现得最多的那个字母在单词中出现的次数。

a=input()
dicts={}
for i in a:
    dicts[i]=dicts.get(i,0)+1
l = sorted(dicts.items(), key= lambda x:x[1])
print(l[-1][0])
print(l[-1][1])

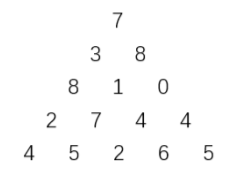
33.

上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。
路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 1。

n = int(input())
list_number = []

for i in range(n):
  list_number.append(list(map(int,input().split())))
max_number = 0
def dfs(deep,key,val,i):
  global max_number
  if deep==n:
    if abs(key)<=1 and val>max_number:
      max_number = val
    return
  dfs(deep+1,key-1,val+list_number[deep][i],i)
  if i<len(list_number[deep])-1:
    dfs(deep+1,key+1,val+list_number[deep][i+1],i+1)

dfs(0,0,0,0)
print(max_number)
方法二：
n = int(input())
list_number = []
for i in range(n):
  list_number.append(list(map(int,input().split())))
for i in range(3, -1, -1):
    for j in range(0, i + 1):
        list_number[i][j] = max(list_number[i + 1][j], list_number[i + 1][j + 1]) + list_number[i][j]
print(list_number[0][0])

34.小蓝最近学习了一些排序算法，其中冒泡排序让他印象深刻。

在冒泡排序中，每次只能交换相邻的两个元素。

小蓝发现，如果对一个字符串中的字符排序，只允许交换相邻的两个字符，则在所有可能的排序方案中，冒泡排序的总交换次数是最少的。

例如，对于字符串 lanlanlan 排序，只需要 111 次交换。对于字符串 qiaoqiaoqiao 排序，总共需要 444 次交换。

小蓝找到了很多字符串试图排序，他恰巧碰到一个字符串，需要 100100100 次交换，可是他忘了吧这个字符串记下来，现在找不到了。

请帮助小蓝找一个只包含小写英文字母且没有字母重复出现的字符串，对该串的字符排序，正好需要 100100100 次交换。如果可能找到多个，请告诉小蓝最短的那个。如果最短的仍然有多个，请告诉小蓝字典序最小的那个。

考虑冒泡排序的复杂度，对于拥有N个字母的字符串，最多需要交换N*(N-1)/2次（完全乱序时）
易知N=15时，有15*14/2=105，即满足100次交换所需的最短字符串有15个字母。
要求字典序最小，那么显然要取a~o这15个字典序最小的字母
  逆向思考，目标字符串经过100次交换后，得到正序字符串abcdefghijklmno，而完全逆序的字符串onmlkjihgfedcba变成正序字符串需要105次交换，那么将完全逆序的字符串交换5次后，便能得到答案。
  而要求字典序最小，那么将j交换5次提到字符串最前面，就得到了最小的情况
zimu = [chr(i) for i in range(ord('z'),ord('a')-1,-1)]
#print(zimu)
count = 0
m = 0
flag = 0
result = ''
for i in range(1,26):
    count = count + i
    if count == 100:
        m = i
        break
    if count > 100:
        m = count - 100
        flag = 1
        break
if flag == 0:
    for i in zimu[-1*i-1:]:
        result = result + i
else:
    result = result + zimu[-1*i+4]
    t = zimu[-1*i+4]
    for i in zimu[-1*i-1:]:
        if i != t:
            result = result + i
print(result)

35.对于一个字符串 S，我们定义 S 的分值 f(S) 为 S中恰好出现一次的字符个数。例如 f("aba")=1，f("abc")=3,f("aaa")=0f("aba") = 1，f("abc") = 3, f("aaa") = 0f("aba")=1，f("abc")=3,f("aaa")=0。

现在给定一个字符串 S0⋯n−1S_{0 \cdots n − 1}S0⋯n−1（长度为 nnn，1≤n≤1051 \leq n \leq 10^51≤n≤105），请你计算对于所有 SSS 的非空子串 Si⋯j(0≤i≤j<n)S_{i \cdots j}(0 ≤ i ≤ j < n)Si⋯j(0≤i≤j<n)，f(Si⋯j)f(S_{i \cdots j})f(Si⋯j) 的和是多少。

方法一：
s = input()
sum = 0
for i in range(0, len(s)):
  for j in range(1, len(len(s) + 1)):
    ss = s[i:j]
    for z in ss:
      if ss.count(j) == 1:
        sum += 1
print(sum)
方法二：
S = input()  #输入字符串
sumvalue =0
#遍历计算一个字符的贡献值
for i in range(0,len(S)):
  numleft =0
  numright = 0
  temp = S[i] #也就是第i个字符的
  loc = i-1
  while(loc>=0 and S[loc]!=temp):
    loc-=1
    numleft+=1
  loc = i+1
  while(loc<len(S) and S[loc]!=temp):
    loc+=1 #一直往上加
    numright+=1
  sumvalue+=((numleft+1)*(numright+1)) #也就是
  # print(numleft,numright)
  # print(((numleft+1)*(numright+1)))
print(sumvalue)
运行时间很长，运行不出来

36.对于一个字母矩阵，我们称矩阵中的一个递增序列是指在矩阵中找到两个字母，它们在同一行，同一列，或者在同一 454545 度的斜线上，这两个字母从左向右看、或者从上向下看是递增的

VLPWJVVNNZSWFGHSFRBCOIJTPYNEURPIGKQGPSXUGNELGRVZAG
SDLLOVGRTWEYZKKXNKIRWGZWXWRHKXFASATDWZAPZRNHTNNGQF
ZGUGXVQDQAEAHOQEADMWWXFBXECKAVIGPTKTTQFWSWPKRPSMGA
BDGMGYHAOPPRRHKYZCMFZEDELCALTBSWNTAODXYVHQNDASUFRL
YVYWQZUTEPFSFXLTZBMBQETXGXFUEBHGMJKBPNIHMYOELYZIKH
ZYZHSLTCGNANNXTUJGBYKUOJMGOGRDPKEUGVHNZJZHDUNRERBU
XFPTZKTPVQPJEMBHNTUBSMIYEGXNWQSBZMHMDRZZMJPZQTCWLR
ZNXOKBITTPSHEXWHZXFLWEMPZTBVNKNYSHCIQRIKQHFRAYWOPG
MHJKFYYBQSDPOVJICWWGGCOZSBGLSOXOFDAADZYEOBKDDTMQPA
VIDPIGELBYMEVQLASLQRUKMXSEWGHRSFVXOMHSJWWXHIBCGVIF
GWRFRFLHAMYWYZOIQODBIHHRIIMWJWJGYPFAHZZWJKRGOISUJC
EKQKKPNEYCBWOQHTYFHHQZRLFNDOVXTWASSQWXKBIVTKTUIASK
PEKNJFIVBKOZUEPPHIWLUBFUDWPIDRJKAZVJKPBRHCRMGNMFWW
CGZAXHXPDELTACGUWBXWNNZNDQYYCIQRJCULIEBQBLLMJEUSZP
RWHHQMBIJWTQPUFNAESPZHAQARNIDUCRYQAZMNVRVZUJOZUDGS
PFGAYBDEECHUXFUZIKAXYDFWJNSAOPJYWUIEJSCORRBVQHCHMR
JNVIPVEMQSHCCAXMWEFSYIGFPIXNIDXOTXTNBCHSHUZGKXFECL
YZBAIIOTWLREPZISBGJLQDALKZUKEQMKLDIPXJEPENEIPWFDLP
HBQKWJFLSEXVILKYPNSWUZLDCRTAYUUPEITQJEITZRQMMAQNLN
DQDJGOWMBFKAIGWEAJOISPFPLULIWVVALLIIHBGEZLGRHRCKGF
LXYPCVPNUKSWCCGXEYTEBAWRLWDWNHHNNNWQNIIBUCGUJYMRYW
CZDKISKUSBPFHVGSAVJBDMNPSDKFRXVVPLVAQUGVUJEXSZFGFQ
IYIJGISUANRAXTGQLAVFMQTICKQAHLEBGHAVOVVPEXIMLFWIYI
ZIIFSOPCMAWCBPKWZBUQPQLGSNIBFADUUJJHPAIUVVNWNWKDZB
HGTEEIISFGIUEUOWXVTPJDVACYQYFQUCXOXOSSMXLZDQESHXKP
FEBZHJAGIFGXSMRDKGONGELOALLSYDVILRWAPXXBPOOSWZNEAS
VJGMAOFLGYIFLJTEKDNIWHJAABCASFMAKIENSYIZZSLRSUIPCJ
BMQGMPDRCPGWKTPLOTAINXZAAJWCPUJHPOUYWNWHZAKCDMZDSR
RRARTVHZYYCEDXJQNQAINQVDJCZCZLCQWQQIKUYMYMOVMNCBVY
ABTCRRUXVGYLZILFLOFYVWFFBZNFWDZOADRDCLIRFKBFBHMAXX

g = []
m = 30
n = 50

for i in range(m):
  g.append(list(input()))

ans = 0
# 统计行
for i in range(m):
  for j in range(n-1):
    for k in range(j+1, n):
      if ord(g[i][j]) < ord(g[i][k]):
        ans+=1
# 统计列
for i in range(n):
  for j in range(m-1):
    for k in range(j+1, m):
      if ord(g[j][i]) < ord(g[k][i]):
        ans+=1
# 统计右下
for i in range(m):
  for j in range(n):
    for k in range(1, m):
      if i+k >= m or j+k >= n:
        continue
      if ord(g[i][j]) < ord(g[i+k][j+k]):
        ans+=1
# # 统计右下
for i in range(m-1, 0, -1):
  for j in range(n):
    for k in range(1, m):
      if i-k < 0 or j+k >= n:
        continue
      if ord(g[i][j]) != ord(g[i-k][j+k]):
        ans+=1
print(ans, end="")

37.A 村的元宵节灯会上有一迷题：

请猜谜 * 请猜谜 = 请边赏灯边猜

小明想，一定是每个汉字代表一个数字，不同的汉字代表不同的数字。

请你用计算机按小明的思路算一下，然后提交“请猜谜”三个字所代表的整数即可。

for i in range(10, 1000):
  a = str(i)
  b = i ** 2
  c = str(b)
  if len(set(list(c))) == 5:
    if a[0] == c[0] and a[1] == c[-1]:
      print(i)
      break

38.小明刚刚看完电影《第 39级台阶》，离开电影院的时候，他数了数礼堂前的台阶数，恰好是 39 级!

站在台阶前，他突然又想着一个问题：

如果我每一步只能迈上 1 个或 2 个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完 393939 级台阶，有多少种不同的上法呢？

请你利用计算机的优势，帮助小明寻找答案

方法一：
num=0
def fun(n,k):
  global num
  if n>39:
    return
  if n==39 and k%2==0:
    num+=1
  fun(n+1,k+1)
  fun(n+2,k+1)
fun(0,0)
print(num)
方法二：
def f(n):
    if n==0:
        return 1
    if n<0:
        return 0
    else:
        return f(n-2)+f(n-3)*2+f(n-4)
print(f(39))
因为只有两次都是一部，或者两次都是两步，或者一次两步一次一步，一次一步一次两步

39.素数就是不能再进行等分的数。比如：2 3 5 7 112\ 3\ 5\ 7\ 112 3 5 7 11 等。 9=3∗39 = 3 * 39=3∗3 说明它可以3等分，因而不是素数。

我们国家在 1949年建国。如果只给你 1 9 4 9 这 4个数字卡片，可以随意摆放它们的先后顺序（但卡片不能倒着摆放啊，我们不是在脑筋急转弯！），那么，你能组成多少个 444 位的素数呢？

比如：1949，4919都符合要求。

请你输出能组成的 4 位素数的个数，不要罗列这些素数!!

别人的方法：
import os
import sys
from math import sqrt
from itertools import permutations as pt
def judge(x):
    if x == 1 or x == 2:
        return False
    for i in range(2, int(sqrt(x)+2)):
        if x % i == 0:
            return False
    return True

ls = ['1', '9', '4', '9']
pt_list = pt(ls)
res = []
ans = 0

for i in pt_list:
    res.append(int("".join(i)))

res = list(set(res))

for i in res:
    if judge(i):
        ans += 1

print(ans)
我的方法：
def isprime(n):
  for i in range(2, n - 1):
    if n % i == 0:
      return False
  else:
    return True

lis1 = ["1", "4", "9", "9"]
lis1.sort()
print(lis1)
sum = 0
for i in range(1499, 9942):
    a = list(str(i))
    a.sort()
    if a == lis1 and isprime(i):
        sum += 1
print(sum)

40.动态规划习题

方法一：
def length_of_lis(nums):
    n = len(nums)
    l = [1] * n 
    for i in reversed(range(n)):
        for j in range(i + 1, n):
            if nums[j] > nums[i]:
                l[i] = max(l[i], l[j] + 1)
    return max(l)
方法二：
def l(nums, i):
    if i == len(nums) -1:
        return 1
    max_len = 1
    for j in range(i + 1, len(nums)):
        if nums[j] > nums[i]:
            max_len = max(max_len, l(nums, j) + 1)
    return max_len
方法三：
memo = {}
def l(nums, i):
    if i in memo:
        return memo[i]
    if i == len(nums) - 1:
        return 1
    max_len = 1
    for j in range(i + 1, len(nums)):
        if nums[j] > nums[i]:
            max_len = max(max_len, l(nums, j) + 1)
    memo[i] = max_len
    return max_len

41.有 nnn 个小朋友围坐成一圈。老师给每个小朋友随机发偶数个糖果，然后进行下面的游戏：

每个小朋友都把自己的糖果分一半给左手边的孩子。

一轮分糖后，拥有奇数颗糖的孩子由老师补给 1 个糖果，从而变成偶数。

反复进行这个游戏，直到所有小朋友的糖果数都相同为止。

你的任务是预测在已知的初始糖果情形下，老师一共需要补发多少个糖果。

# 请在此输入您的代码
N = int(input())  # 孩子的个数
s = list(map(int, input().split()))  # 每个孩子的糖果数
ans = sum(s)  # 开始总的糖果数
a = s[0] // 2   # 上一个孩子给下一个孩子的糖果数
while len(s) != s.count(s[0]):  # 当每个人糖果数不一样时执行
    for i in range(N):
        if i + 1 == N: 
            # 让最后一个孩子的下一个指向第一个孩子
            i = -1
        # 分糖果
        s[i+1], a = s[i+1] + a - s[i+1] // 2, s[i+1] // 2
        if s[i+1] % 2 != 0:  # 奇数时加1
            s[i+1] += 1
ans = sum(s)-ans # 补发的糖果数
print(ans)

42.小明开了一家糖果店。他别出心裁：把水果糖包成 4 颗一包和 7 颗一包的两种。糖果不能拆包卖。

小朋友来买糖的时候，他就用这两种包装来组合。当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。

你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是 17。大于 17 的任何数字都可以用 4 和 7 组合出来。

本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

m, n = map(int, input().split())
dp = [0 for _ in range(max(n, m) + 1)]
dp[max(n, m)] = 1
i = min(n, m)
while i <= max(n, m):
    dp[i] = 1
    i += min(n, m)
i = max(n, m) + 1
while i <= n * m:
    if dp[i - n] == 1 or dp[i - m] == 1:
        dp.append(1)
    else:
        dp.append(0)
        count = i
    i += 1
print(count)

43.矩阵转置

m, n = map(int, input().strip().split(" "))
lis = []
for i in range(m):
  lis.append([int(x) for x in input().strip().split(" ")])

lis1 = []
for j in range(n):
  lis2 = []
  for i in reversed(range(m)):
    lis2.append(lis[i][j])
  lis1.append(lis2)
# n, m = map(int, input().strip().split(" "))
# lis = []
# for i in range(n):
#     lis.append([int(x) for x in input().strip().split(" ")])
print(lis1)

44.我们称一个字符串 SSS 包含字符串 TTT 是指 TTT 是 SSS 的一个子序列，即可以从字符串 SSS 中抽出若干个字符，它们按原来的顺序组合成一个新的字符串与 TTT 完全一样。

给定两个字符串 SSS 和 TTT，请问 TTT 中从第一个字符开始最长连续多少个字符被 SSS 包含？

a = input()
b = input()
count = 0
for i in b:
  if i in a:
    a = a[a.index(i):]
    count += 1
print(count)

45.在一个 nnn 行 mmm 列的方格图上有一些位置有地雷，另外一些位置为空。

请为每个空位置标一个整数，表示周围八个相邻的方格中有多少个地雷。

import os
import sys
方法一：
n,m=(int(x) for x in input().split(" "))

lst = [[0 for _ in range(m)] for _ in range(n)]
ans = [[0 for _ in range(m)] for _ in range(n)]

for i in range(n):
    lst[i]= [int(x) for x in input().split(" ")]

for x in range(n):
  for y in range(m):
    if lst[x][y]==0:
      count = 0
      for p in range(x-1,x+2):
        for q in range(y-1,y+2):
          if 0<=p<n and 0<=q<n:
            if lst[p][q]==1:
              count+=1
      ans[x][y]=count
    else:
      ans[x][y]=9

for x in range(n):
  for y in range(m):
    print(ans[x][y],end=' ')
  print()
方法二：

n, m = map(int, input().split())
l = []
for _ in range(n):
    l.append(list(map(int, input().split())))
# print(l)
ans = [[0 for _ in range(m)] for _ in range(n)]

for i in range(n):
    for j in range(m):
        s = 0
        if l[i][j] == 1:
            ans[i][j] = 9
        else:
            for k in range(i-1, i+2):
                for h in range(j-1, j+2):
                    if 0 <= k < n and 0 <= h < m:
                        s += l[k][h]
            ans[i][j] = s
for i in range(n):
    print(" ".join(str(x) for x in ans[i]))
还是不是很懂map的用法

46.由 1 对括号，可以组成一种合法括号序列：()。

由 2对括号，可以组成两种合法括号序列：()()、(())。
由 4 对括号组成的合法括号序列一共有多少种？

s=['m','n']
t=[]
for a in s:
    for b in s:
        for c in s:
            for d in s:
                for e in s:
                    for f in s:
                        if list((a,b,c,d,e,f)).count('m')==3: 
                          if list((a,b,c,d)).count('n')!=3:
                            if list((a,b))!=['n','n']:
                              t.append(list((a,b,c,d,e,f)))                       
print(len(t))

47.实现一个算法得到乌托邦树的高度。介绍如下：

乌托邦树每年经历 2 个生长周期。每年春天，它的高度都会翻倍。每年夏天，它的高度都会增加 1 米。

对于一颗在春天开始时种下的高 1 米的树，问经过指定周期后，树的高度为多少。

n = int(input())
height = 1
for i in range(n):
  if (i + 1) % 2 == 1:
    height *= 2
  else:
    height += 1
print(height)
递归实现
num = eval(input())
def tree(n):
    if n == 0:
        return 1
    elif n == 1:
        return 2
    elif n%2:
        return 2*(tree(n-2) + 1)
    else:
        return 2*tree(n-2) + 1
print(tree(num))

posted @ 2021-04-19 18:00 W-forever 阅读(1457) 评论(0) 收藏举报

刷新页面返回顶部

W-forever